基于并线行为识别的自适应巡航控制方法*

蔡英凤，吕志军，孙晓强，王 海，刘擎超，陈 龙，袁朝春

（1.江苏大学汽车工程研究院，镇江 212000；2.江苏大学汽车与交通工程学院，镇江 212000）

前言

自适应巡航控制（adaptive cruise control，ACC）是一种通过车载测量设备获得与前车的实时车间距及速度等信息，应用加速度优化算法控制车辆与前车保持稳定车间时距行驶的车辆纵向跟驰控制技术。然而由于实际交通环境下，车辆密集和频繁换道等原因，导致ACC系统出现对并线车辆不敏感、制动过晚或过急等问题，因此基于并线车辆行为识别的自适应巡航控制研究具有重要的现实意义。

旁车道车辆向ACC车辆所在车道内并线行驶是实际交通环境中较常见的一种工况，自适应巡航控制系统须对旁车的并线行为具备必要甚至提前的反应能力，以保障ACC车辆的行驶安全［1］。目前的自适应巡航控制系统大都只针对主车道内的主目标车辆进行控制［2-3］，而ACC车辆的控制功能往往只有在旁车完全进入主车道后引起主目标车辆变化时才能发挥作用，因此传统ACC车辆更新目标滞后且不能将旁车并线过程中的行驶数据充分应用于控制。当ACC车辆在主车道内检测到并线后的旁车时，控制器往往会输出大强度制动以避免碰撞的发生，这不仅会影响到驾乘人员的舒适性，且会对后续车辆的安全行驶产生影响。

自适应巡航控制系统多采用分层控制结构［4］。上层控制器根据当前行驶环境，输出安全跟车所需期望加速度；下层控制器依据上层得出的期望加速度，通过节气门和制动器的切换控制，使车辆的实际加速度能追踪上层控制器期望加速度。目前该方向的研究主要集中于系统的稳定性与环境适应性，如Haroon等［5］提出在stop&go场景下的巡航控制策略。刘正国［6］研究了包含车道关系识别模型和旁车道车辆换道切入识别模型的ACC目标识别方法。同样考虑动态跟踪性、燃油经济性、跟驰安全性等多目标的协调式ACC也引起了广泛关注，如李想等［7］提出基于改进线性二次型最优控制的自适应巡航控制算法研究。控制方法方面，近年来，由于模型预测控制［8］可对系统未来动态行为进行预测与具有显式处理约束的能力等优势，其广泛应用于自适应巡航控制研究。吴光强等［9］设计了一种多目标鲁棒跟车控制算法，兼顾了舒适性和安全性要求。Zhu等［10］结合熟练驾驶员经验，使用车间反应时距定量描述自车何时对目标车辆做出反应，并设计了模型预测控制器。张亮修等［11］基于模型预测控制理论将多目标ACC系统控制算法转化为带有多个约束的在线二次规划问题，相比线性二次型调节器算法，其百公里油耗与追踪误差指标均有明显下降。然而上述模型预测控制算法中多目标的权值须根据不同的驾驶场景进行调整，但车辆行驶场景频繁变化，在线调整预测控制器的权重是不切实际的［12］。此外，车辆自适应巡航涉及的多个性能在控制中往往是相互冲突的，所有性能不能同时达到最优。

本文中提出的基于并线车辆行为识别的自适应巡航控制系统，利用并线车辆的历史轨迹对其并线行为进行识别，将并线行为识别集成到MPC控制框架中，在并线车辆尚在旁车道时就对ACC车辆进行一定的速度控制，解决了常规自适应巡航系统响应过晚过急的问题；同时，考虑不同类型驾驶员在并线时不同的驾驶特性可提高控制模型的适应性，并能有效提高乘车舒适性，降低行车风险。

1 自适应巡航控制系统整体设计

提出的基于并线行为识别的自适应巡航控制系统框架如图1所示。首先，提取并线车辆的历史轨迹信息及环境信息，将其输入到行为识别器的长短时记忆（long short⁃term memory，LSTM）网络循环体，LSTM单元体通过当前时刻的输入和历史轨迹信息的隐藏状态来更新当前时刻的隐藏状态，通过这种方式，LSTM学习历史轨迹序列中的规律，最终输出并线、直行两种意图类别及其概率。而后，当行为识别器输出的车辆并线概率超过一定阈值时，即识别出并线行为，ACC车辆的模型预测控制器在并线车辆尚未到达换道点时提前结合并线车辆运动数据、考虑并线行为驾驶特性的预测模型、性能指标与约束条件、理想点法进行期望加速度最优化求解，使并线行为尚未成功时即对ACC车辆进行速度控制，避免了因旁车并线而导致的车辆运动不稳定性。

图1 自适应巡航控制系统框架

2 并线行为识别

实际交通场景中各车辆的行为具有多样性和不确定性。总的来说，在结构化道路中可分为3种典型行为：向左换道、保持车道与向右换道。对于ACC车辆，并线行为通常表现为左前方邻车道车辆向右并线或右前方邻车道车辆向左并线至ACC车辆前方。

随着长短时记忆网络在语音识别、机器翻译等领域取得一系列重大突破［13］，其在应对时序问题时展现出强大的信息挖掘能力和深度表征能力，轨迹序列也是一种时间序列，故本文采用基于长短时记忆网络构建的并线行为识别器，其架构如图2所示。定义主车为EV，主车前方车辆为EVF，并线车辆为CV，并线车辆的前方车辆为CVF，如图3所示。将车辆的历史信息I(t)作为输入，它包括并线车辆、并线车辆与周边车辆交互和并线车辆相对于车道线的历史信息，可表示为I(t)={Se EM}，式中并线车辆的历史信息S e={vy(CV)φ}，其中vy(CV)、φ分别为并线车辆的横向速度和航向角；并线车辆与周边车辆的交互信息E包括并线车辆前方车辆、主车和主车前方车辆3辆车的历史轨迹信息，这些历史轨迹包括纵向相对距离与纵向相对速度，{dCV-CVFdCV-EVdCV-EVF}、{ΔvCV-CVFΔvCV-EVΔvCV-EVF}分别表示并线车辆相对于CVF、EV、EVF的纵向相对距离和纵向相对速度；并线车辆相对于车道线的信息M={yCV}，其中yCV为并线车辆相对于并线方向车道线的横向距离。考虑到在实际场景中的应用，E的相关数据可由主车的毫米波雷达直接获得或经过运算间接获取，S e、M的相关数据可由前视摄像头提供。

图2 并线行为识别器架构

图3 车辆定义

并线行为识别器将并线车辆、与之交互的其他车辆和道路信息组成的整体视为研究对象，根据其交互式信息理解车辆运行规律，使模型理解车-车-路之间的交互行为，并对旁车的并线行为进行预判。采用动态滑动时窗的方法获取输入量I(t)，通过具有128个神经元、激活函数为ReLU的全连接层，将经处理后的量输入长短时记忆网络循环体。LSTM单元体通过遗忘门的sigmoid单元保留历史轨迹信息中所包含的隐藏状态信息，再通过输入门将前一层隐藏状态的信息和当前输入的信息传递到sigmoid函数与tanh函数中，以此更新细胞状态，最后通过输出门来确定下一个隐藏状态的值，并传递到下一个时间步长中去。具体的，在每一时刻t，LSTM单元体读取当前时刻的输入I(t)和上一时刻以前历史轨迹信息的隐藏状态ht-1，以此更新当前时刻的隐藏状态ht，即ht=f(ht-1I(t))，LSTM通过这种方式学习历史轨迹序列中的规律，经过Softmax层后，输出概率矩阵Ω={p(c1|I)p(c2|I)}，其中c1、c2分别代表并线、直线两种意图类别，p(ci|I)(i=1，2)分别代表并线、直线的概率，其中进而对输出的概率做一逻辑判断：规定并线的确信阈值为80%，当并线的行为意图小于确信阈值时，默认输出行为类别为直线行驶c2，而当并线的行为意图大于确信阈值时，输出并线行为类型c1。

本文中所使用的车辆轨迹数据集源于德国亚琛工业大学汽车工程研究所2018年提出的high D数据 集［14］。 与 较 为 经 典 的NIGSIM（next generation simulation）轨迹数据集相比，high D数据集能够有效解决假性重叠碰撞的问题，并提供了更为完整的车辆状态信息，为本文研究的车辆交互识别提供了丰富的研究素材。

由于直线行驶工况远多于并线工况，所以提取车辆的车道保持序列数目显然远大于并线序列，为防止训练过程中出现过拟合，每个行为序列集中选取的序列数量相同，使样本分布均匀，最终从760个目标车辆中提取出10 000个样本序列（直线行驶和并线两种工况的样本皆为5 000个），按8∶2的比例将数据集随机划分为训练集和测试集。为体现这一动态调整过程，从测试集中选择一段具有代表性的向左并线行驶的完整轨迹序列。图4示出并线车辆接近换道点过程中，行为识别模块实时输出两类驾驶行为的概率。

图4 并线行为识别结果

3 自适应巡航控制系统设计

3.1 系统建模

如图5所示，根据两车间的纵向运动关系，定义如下两种车间状态变量：

图5 车辆纵向跟车模型

式中：Δd(t)为实际车间距d(t)与期望车间距ddes(t)的车间距误差，其中车间距为主车车头至目标车辆车尾的距离；Δv(t)为两车相对速度；vPV(t)和vEV(t)分别为目标车辆和ACC车辆的速度。本文中采用固定车间安全时距模型［15］，则ACC车辆的期望车间距ddes(t)=τh⋅vEV(t)+d0，其中τh为固定车间时距；d0为最小安全车距。

在设计ACC系统上层控制器时，一般可以认为实际加速度aEV和期望加速度aEVdes满足如下的关系［16］：

式中：Ts为系统采样周期；τL为惯性环节时间常数。

建立以[Δd(t)Δv(t)aEV(t)]T为状态变量，期望加速度aEVdes(t)为控制变量的线性离散状态空间方程：

式中：x(t)=[Δd(t)Δv(t)aEV(t)]T；u(t)=aEVdes(t)；ρ(t)=aPV(t)为前车加速度扰动；A、B、G、C为状态空间方程系数矩阵，

便于对控制量进行精确约束，将式（3）改写为增量形式：

式中：Δx(t)=x(t)-x(t-1)；Δu(t)=u(t)-u(t-1)；Δρ(t)=ρ(t)-ρ(t-1)。

基于t时刻的车辆状态信息，对未来的i(i=1，2，…，Np)时刻的输出状态进行预测，定义Np步预测输出序列和Nc步控制输入增量序列为

则系统未来Np步的预测方程可以表示为

3.2 不同并线行为下的参考量

由于不同类型驾驶员在换道并线时具有不同的驾驶特性［17］，即会表现出快速与慢速的并线行为，轨迹示意图如图6所示。文献［18］中根据实际道路运行情况调查了车辆的换道时间，得出换道时间在2-3 s的概率为22.76%，在3-5 s的概率为57.93%，大于5 s的概率为19.31%，因此本文根据车辆的换道时间划分不同的并线行为，小于3 s的为快速并线，3-5 s的为正常并线，大于5 s的为慢速并线。在ACC车辆的控制策略中有必要考虑并线行为的风格，当面对正常并线时，ACC车辆应兼顾行车安全与乘车舒适性；当面对快速并线动作时，ACC车辆应提前快速减速以保持安全车距以避免碰撞或给乘车人带来的心理压力；当面对缓慢并线动作时，ACC车辆应逐渐减速以提高乘车舒适性。

图6 不同并线风格示意图

换道并线过程中，可通过车辆横向位置的变化来表征不同的并线行为。本文中采用驾驶员预瞄模型［8］预测并线过程中的横向位置变化，如图7所示。预测车辆未来的位置在预瞄点处，那么车辆的横向位置可由当前横向位置、纵向速度和航向角偏差来计算：

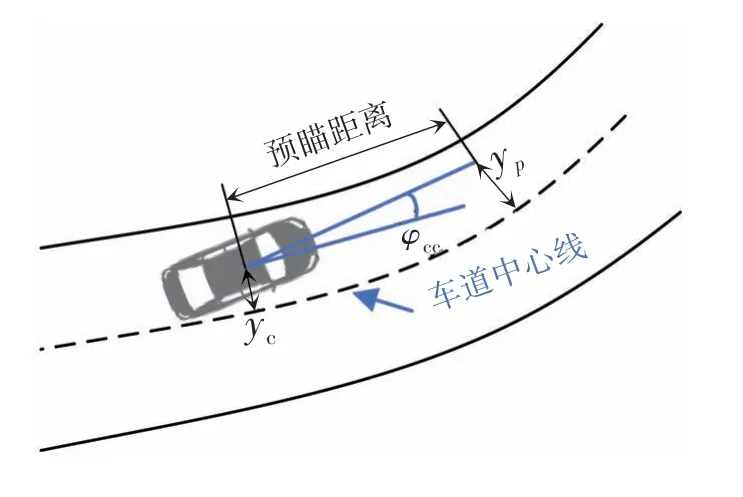
图7 驾驶员预瞄模型

式中：yp为预瞄点的横向位置；yc为车辆的当前横向位置；vxc为车辆纵向速度；φec为车辆航向角与期望航向角的误差；τ为预瞄时间；预瞄距离可由vxcτ表示。

因此，预测的并线车辆的纵向位置为xCV(t+i+1|t)=xCV(t+i|t)+TsvCV(t+i)，预测的并线车辆的横向位置可表示为yCV(t+i+1|t)=yCV(t+i|t)+TsvCV(t+i)φCV(t+i)那么，当并线车辆已经完成并线动作后，其预测时域内的纵向位置偏差可表示为

当已经识别出换道行为，正在进行并线行为时，须考虑并线车辆横向位移对ACC车辆的影响，通过并线车辆的横向位置来调整纵向跟车，其预测时域内的纵向位置偏差［19］可表示为

3.3 性能指标和I/O约束处理

为提高ACC的性能，考虑跟随性能、舒适性能和能耗性能3类性能指标及约束条件。

（1）跟随性能指标

ACC车辆不断调整车速与车间距，使两车纵向距离收敛于期望距离，本车速度收敛于前车车速，取车间距误差和相对速度的矩阵二范数之和作为跟随性能指标JT［20］，表示为

前车行驶时，车间距误差和速度误差应处于合适范围内，采用不等式约束来界定车间距误差和速度误差［21］的范围为

式中：Δdmax和Δdmin分别为车间距误差的上下界；Δvmax和Δvmin分别为车速误差的上下界。

（2）舒适性能指标

一方面，在跟车过程中，驾驶员期望缓加速、缓减速，从而保证乘坐舒适性，故采用控制量增量的矩阵二范数来定义舒适性指标JC［22］：

另一方面，车辆实际纵向加速度、期望纵向加速度和期望加速度的增量应保持在一定的范围内［23］：

式中：aEVmax和aEVmin分别为加速度数值的上下界；umax和umin分别为控制量的上下界；Δumax和Δumin分别为控制量增量的上下界。

（3）能耗性能指标

采用燃料消耗JF来表征能耗性能指标［24］：

式中Ccruise(t)和Caccel(t)分别为在稳定速度vEV(t)下燃料的消耗量和在车速vEV(t)有加速度时燃料额外的消耗量，可用下面公式描述：

式中bi(i=0，…，3)和cj(j=0，…，2)是车辆的燃料消耗参数。对于普通车辆，通常可取b0=0.1569，b1=2.45×10-2，b2=-7.415×10-4，b3=5.975×10-5，c0=7.224×10-2，c1=9.681×10-2，c2=1.075×10-3［24］。

由于以上3种性能是相互冲突的，本文中使用结合理想点［25］和模型预测控制的方法来设计多目标预测巡航控制器。定义成本矢量为J=[JTJCJF]T，为计算出J的理想点，根据理想点的多目标方法分析了本车一些稳定状态的情形。对于JT，如果车辆的相对速度等于零，且车间间距等于期望的车间距，那么本车将达到行驶的最佳稳定状态。此外，函数JT相对于变量vEV(t)是凸函数［26］，且在所有t≥0时刻满足JT≥0，因此在所有t≥0时刻，JT∗(t)=0是函数JT可取的最小值。JC是与变量vEV(t)无关的函数，当车辆匀速行驶时，JC∗(t)=0是函数JC可取的最小值。而JF相对于变量vEV(t)是非凸函数，通过下面的优化问题可以得到JF的最小值：

因此，在t时刻，成本函数的理想点可定义为但由于各性能指标相互冲突，所以该理想点无法取得，为此本文引入了一个折衷的成本函数：

式中‖⋅‖2表示向量的2范数，即最大限度地减小成本矢量J(t)到其理想点J∗(t)的矢量距离。

3.4 求解与滚动优化

在每个时刻t，通过在线求解下面的有限时域最优控制问题即式（20）得到多性能预测巡航控制器的控制输出。

上述优化控制问题是一个线性和非凸函数的优化控制问题，采用文献［25］中的基于摄动的序列二次规划算法（InPA-SQP）进行求解。在每个采样周期内，利用式（20）进行MPC控制器求解得到控制时域内的控制输入增量序列：

4 控制系统仿真分析

基于本文提出的自适应巡航控制器，建立Matlab/Simulink仿真系统模型，为验证上述自适应巡航系统的可行性与优越性，验证了3种仿真工况：（1）定速工况；（2）跟车行驶工况；（3）旁车道车辆并线工况（正常、快、慢）。Only⁃MPC采用模型预测控制，UPM⁃MPC为结合理想点法的模型预测控制，Pre⁃UPM⁃MPC为结合并线识别与理想点法的模型预测控制。控制器所采用的参数如表1所示。

表1 控制器参数

（1）定速工况

定速工况下，初始时刻ACC车辆以72 km/h初速度行驶，设定目标速度为90 km/h。定速工况的仿真结果如图8所示。

图8 定速工况仿真结果

由图8可知，UPM⁃MPC与Only⁃MPC均于8 s左右收敛于90 km/h，但UPM⁃MPC的峰值加速度比Only⁃MPC低10.03%，且Only⁃MPC的速度超调率为1.44%，而UPM⁃MPC未产生超调，两者能耗相差不大。结果表明，在定速巡航工况下，UPM⁃MPC算法可有效降低控制量峰值，减少超调现象。

（2）跟车行驶工况

跟车行驶工况下，初始时刻ACC车辆以72 km/h的初速度行驶，目标车辆在ACC车辆前方40 m处以90 km/h的初速度变速行驶，其加速度以正弦曲线变化，幅值为0.6 m/s2，周期为8 s。跟车行驶工况的仿真结果如图9所示。

图9 跟车行驶工况仿真结果

由图9可知，UPM⁃MPC对前车的速度变化反应更加灵敏且加速度曲线更加平顺，稳定跟车后其速度平均跟随误差约为0.39 km/h，比Only⁃MPC的0.51 km/h低约23.53%，稳定跟车后UPM⁃MPC的平均跟车误差为0.717 m，比Only⁃MPC的1.282 m低约0.565 m，两者能耗基本相同。结果表明，在跟车巡航工况下，UPM⁃MPC算法在稳定跟车后跟随误差更小，具有更好的跟车性能。

（3）并线工况

正常并线工况下，ACC车辆以60 km/h的车速巡航行驶，初始时刻其前方15 m处旁车以45 km/h的车速从旁车道并线，约2.3 s时到达换道点。正常并线工况仿真结果如图10所示。

图10 正常并线工况仿真结果

由图10可知，Pre⁃UPM⁃MPC在旁车道车辆到达换道点前1.2 s开始提前减速，其峰值减速度出现在4.3 s处，为-1.17 m/s2，而UPM⁃MPC与Only⁃MPC的峰值减速度为-1.74和-2.13 m/s2，且Pre⁃UPM⁃MPC的加速度变化率较小，曲线更加光顺，不存在急减速的情况，并且能耗也最低。

慢速并线工况下，ACC车辆以60 km/h的车速巡航行驶，初始时刻其前方15 m处旁车以45 km/h的车速从旁车道并线，约3 s时到达换道点。慢速并线工况仿真结果如图11所示。

图11 慢速并线工况仿真结果

由图11可知，Pre⁃UPM⁃MPC在旁车道车辆到达换道点前1.8 s开始进行减速，其峰值减速度出现在5 s处，为-0.961 m/s2，而UPM⁃MPC与Only⁃MPC的峰值减速度为-1.615和-2.112 m/s2，且Pre⁃UPMMPC的减速度曲线更加光顺，不存在突然施加制动力的情况，但能耗最大。

快速并线工况下，ACC车辆以60 km/h的车速巡航行驶，初始时刻其前方15 m处旁车以45 km/h的车速从旁车道并线，约1.5 s时到达换道点。快速并线工况仿真结果如图12所示。

由图12可知，Pre⁃UPM⁃MPC在旁车道车辆到达换道点前0.6 s开始进行减速，整个减速过程经历3.785 s，其峰值减速度出现在2.23 s处，为-2.805 m/s2，而UPM⁃MPC与Only⁃MPC的峰值减速度均达到系统允许的最小值-3 m/s2。Pre⁃UPM⁃MPC在UPM⁃MPC与Only⁃MPC开始减速之前已降低了约4%的车速，且超调最小，表明其跟踪性能最好，且其能耗最低。

图12 快速并线工况仿真结果

仿真结果表明，引入并线车辆行为识别的自适应巡航系统可在并线车辆到达换道点前对ACC车辆提前至少0.6 s进行制动，加速度曲线不存在突跃的情况且曲线更加平滑，减少紧急制动情况的发生，有效降低制动强度。在不同特性的并线行为中，自适应巡航系统可根据旁车并线风格的不同而求解出适应当前状态的加速度曲线。在慢速并线场景中，系统在识别出并线行为时开始施加较小的制动力，当车辆到达换道点附近时制动力达到最大，且加速度曲线连续光顺，保障了乘坐舒适性；在快速并线场景中，系统对并线行为提前、快速响应，制动力在开始实施后约1.3 s才达到最大，保证安全的前提下提高了舒适性。

5 实车试验

为验证所设计的自适应巡航控制方法在实车上的控制效果，基于艾瑞泽智能驾驶平台进行实车试验。试验平台架构如图13所示，主车以艾瑞泽汽车为基础，针对制动系统和转向系统进行线性改装：加速度指令转化为对应的加速踏板行程指令，制动指令转为制动压力信号发送给真空助力器以控制原车制动缸；车载处理器采用Nuvo⁃6108GC工控机，支持在Matlab/Simulink环境下的代码生成与下载，可以实时显示与在线调试；前向目标识别系统采用Minieye摄像头与Delphi毫米波雷达融合的方式，可有效识别各个车道上共17个前向目标并获取其运动状态信息。在Matlab中搭建不同的算法模型，并将其编译下载到控制器中，模型输入为ACC车辆、毫米波雷达、摄像头的CAN总线信号，输出为模型决策的期望加速度，并由下层PID控制器将其转化为加速踏板与制动踏板行程指令，控制车辆纵向运动，从而进行算法的实车试验。

图13 试验平台架构

实车试验场景如图14所示，试验路况为标准化单向可跨越三车道，只有主车作为被控对象，其他车辆均为人类驾驶。试验工况与第4节中的并线工况一致，图15、图16分别为慢速和快速并线的试验结果。

图14 实车试验场景

图15 慢速并线工况实车试验结果

图16 快速并线工况实车试验结果

实车试验结果表明，引入并线行为识别的控制方法在以上两种工况中均可进行提前制动，速度更加平稳，始终保持较大车间距，同时控制系统对不同类型的并线行为有较好的适应性，实车试验结果与仿真结果基本一致。

6 结论

提出一种基于并线车辆行为识别的自适应巡航控制方法，利用并线车辆的历史轨迹和周围环境对并线行为进行识别，将车辆并线识别集成到模型预测控制的框架中，在并线车辆到达换道点之前对ACC车辆进行一定的速度控制，避免控制器输出大强度制动甚至碰撞的发生。同时，引入驾驶特性可提高控制模型在面对不同并线行为时的适应性。今后的研究工作将主要针对两个方面，第一是利用真实路况下无人驾驶试验平台与软件模拟平台采集的车辆轨迹数据直接进行并线轨迹预测，并将其融合到模型预测控制中；第二是进一步研究人类驾驶员就并线行为的反应特性。