考虑驾驶员操作误差的混合动力汽车队列生态驾驶控制*

钱立军，陈 健，吴 冰，宣 亮，陈 晨，陈亮亮

（合肥工业大学汽车与交通工程学院，合肥 230009）

前言

随着全球车辆总数的增加，城市交通特别是交叉路口面临严重的交通拥堵和环境污染问题。根据德克萨斯州交通运输研究所报告，2017年美国城市交通因交通拥堵造成88亿h的浪费以及33亿加仑的燃油消耗，交通拥堵造成的经济损失达1 660亿美元［1］。同时由于拥堵，驾驶员对车辆进行频繁加减速以及怠速，会排放出更多尾气，加重环境污染。据统计，2018年我国交通运输消耗60%的石油资源，排放温室气体占比达14%［2］。随着全球范围内节能减排的政策法规日益严格，提高城市交叉路口通行能力和降低车辆燃油消耗显得十分重要。

智能网联技术的发展为提高城市交通的安全、通行效率和燃油效率提供新的机遇。在智能网联环境下，车辆与车辆、交通设施之间可以通过车-车（V2V）或者车-设施（V2I）通信技术进行实时通信。因此，接近交叉路口的车辆可以获取信号灯时间、前方交通量、建议车速、道路坡度等的交通信息来优化自身的速度轨迹，从而降低燃油消耗和行程时间［3-5］。近几年来，基于智能网联技术的混合动力汽车生态驾驶控制方法由于其燃油效率高和排放污染少的特点而受到广泛的关注和研究。文献［6］中提出了一种混合动力汽车双层优化方法，该方法集成上层的车辆速度控制和下层的能量管理，通过优化车辆速度和动力传动系统来提高混合动力汽车的燃油经济性。针对不同的地形，文献［7］中设计了一种集成优化控制器以最小化在起伏地形上混合动力汽车的燃油消耗，该控制器利用道路未来速度限制和坡度信息，采用庞特里亚金最小原理来优化车辆加速度和动力传动系统功率分配。然而上述方法多用于优化单车的燃油经济性，而没有考虑前后车辆之间的相互影响。在跟车场景中，前车的速度变化往往会对后车产生较大的影响。为此，文献［8］和文献［9］中分别提出了考虑前车状态的车辆生态自适应巡航控制和预测巡航控制。另外，也有学者对交叉路口混合动力汽车队列生态驾驶控制方法进行研究，以实现车队整体燃油效率最优。文献［10］中提出了一种分层控制策略用于优化城市交叉路口混合动力汽车队列的燃油经济性，利用交通信号灯信息和前方车辆状态信息优化车队中目标车辆的速度轨迹，从而最小化车辆燃油消耗和避免红灯停车。文献［11］中提出了一种考虑混合动力汽车队列系统非线性特性的分层控制方法，上层控制器通过建立鲁棒预测模型来优化队列的稳定性和燃油经济性，下层控制器基于切换控制规则实现发动机和电机协调控制，仿真结果验证了该方法的有效性。目前，混合动力汽车生态驾驶控制研究多假设车辆全部为智能网联汽车，较少考虑传统人类驾驶汽车的影响。有研究表明全网联自动驾驶环境将迟至2060年实现［12］。在人类驾驶汽车与网联汽车并存环境下，如何实现混合动力汽车生态驾驶控制的研究较少。另外，对于人类驾驶的网联汽车，由于存在操作误差和不同驾驶风格，驾驶员可能无法完全跟随优化后的车速轨迹行驶，因此，车辆燃油经济性并不能实现最优。

为解决上述问题，本文中提出一种部分车辆联网环境下交叉路口混合动力汽车队列的生态驾驶控制方法。该方法采用分层控制架构，上层控制器考虑驾驶员操纵误差的影响，基于随机模型预测控制算法优化车队中网联汽车速度轨迹；下层控制器采用自适应等效燃油消耗最小化策略优化车辆发动机与电池的功率分配。最后通过仿真验证了控制算法的有效性。

1 分层生态驾驶控制架构

所研究的城市交叉路口场景如图1所示，并考虑人类驾驶的传统汽车和网联汽车混行的情况。当网联汽车进入到交叉路口的有效通信范围（半径为R）时，可以与路边单元进行信息交互，获取交通信号信息和后方邻近车辆的位置和速度等信息。当后方存在跟随的车辆时，网联汽车作为领头车与跟随车辆组成一个队列行驶，主要目的是通过对网联汽车车速优化控制达到对跟随车辆中人类驾驶汽车的间接控制，从而减少其加减速次数和时长，避免红灯停车，实现整个车队的燃油经济性最优。为了降低控制算法设计的复杂度，做出如下假设：（1）车道上的车辆均为由人类驾驶的直行车辆，不考虑左转和右转车辆以及无人驾驶车辆；（2）同一道路上的车辆遵循先进先出规则，不存在超车现象；（3）不考虑通信的延迟和丢包；（4）路边单元能够通过传感技术（如雷达、摄像头等）获取车队中传统人类驾驶汽车的位置和速度等信息。

图1 研究场景

所提出的分层生态驾驶控制架构主要包括上层控制器和下层控制器两部分。如图2所示，对于每一个混合动力汽车队列，上层控制器根据从路边单元获取的道路信息、交通信号信息和邻近车辆信息来优化车队中网联汽车的速度轨迹，在保证车辆安全和通行效率前提下降低车队中所有网联汽车和人类驾驶汽车的燃油消耗，即优化目标是提升整个车队的燃油经济性。上层控制器将优化后的车速信息发送给网联汽车，由人类驾驶员通过操纵车辆来跟随该优化车速。对于车队内每一辆混合动力汽车，下层控制器获取车辆的实际车速，通过优化汽车发动机与电池的功率分配来最小化等效燃油消耗，并将车辆的驱动与制动能量回收效率反馈给上层控制器以修正上层控制器中的混合动力汽车燃油消耗模型。

图2 分层控制架构

2 系统建模

2.1 Gipps跟车模型

本文中采用Gipps跟车模型［13］来描述传统人类驾驶汽车的运动。在该模型中车辆通过改变自身车速来与前车保持安全的车头时距，从而避免车辆碰撞，且该模型不需要进行参数校准，计算效率较高。车辆的速度可通过式（1）～式（3）计算。

式中：i为跟随车辆；j为前方领头车辆；τ为反应时间，与仿真步长相等；为车辆在一个时间步长内能够加速得到的最大速度；为车辆的最大安全速度；vi，des为车辆i的期望车速；vi(t)和vj(t)为前后车辆在t时刻行驶的速度；si(t)和sj(t)为前后车辆在t时刻行驶的距离；amin和amax为车辆最小和最大舒适加速度；l为车身长度；h为车辆静止时的最小安全距离。

2.2 驾驶员误差模型

在本文中，驾驶员误差被定义为驾驶员操纵车辆跟随最优建议车速时车辆实际加速度与上层控制器计算得到的最优加速度之间的差值［14］。由于该加速度误差具有马尔可夫性质，即下一时刻误差仅与当前时刻误差相关，可采用马尔可夫链模型来描述驾驶员误差变化。将驾驶员误差离散成为有限数量状态，其转移概率矩阵为

式中：τxy为驾驶员误差从状态x转移到状态y的概率；Ne为驾驶员误差状态的数量，x，y≤Ne。

2.3 上层控制器数学模型

根据假设（1），交叉路口的车辆均为直行车辆，因此上层控制器只考虑车辆的纵向运动。车队中任意车辆的纵向动力学模型［14］如式（5）～式（7）所示。

式中：Mi、CD、ρa、Av、f和θ分别为车辆的质量、空气阻力系数、空气密度、车辆的迎风面积、滚动阻力系数和路面坡度；g为重力加速度；m为车队的车辆数；ai为车辆的实际加速度；ai，opt为上层控制器计算的车辆最优加速度；ai，err为由驾驶员操纵误差导致的车辆加速度误差。本文中只考虑网联汽车的驾驶员误差，对于传统人类驾驶汽车，其实际加速度即为跟车模型计算的加速度。

上层控制器的优化目标是最小化车队单位距离的燃油消耗，该问题可由式（8）～式（13）来描述。

2.4 下层控制器数学模型

对于混合动力汽车，汽车消耗的功率可以通过发动机和电池来提供。下层控制器的目标是在满足车辆功率需求下，合理分配发动机和电池功率来最小化等量燃油消耗。下层控制问题可由式（14）～式（18）描述。

式中：SOC(t)为电池荷电状态；u(t)为电池的输出功率；mfuel(u(t))为燃油消耗率；t0和tf分别为驾驶循环的初始时刻和结束时刻；I(t)为充放电时流过电池的电流；Qmax为电池容量；SOCmin和SOCmax分别为最小和最大SOC值；Pbat，min和Pbat，max分别为最小和最大电池输出功率。

3 车辆速度优化与能量管理方法

3.1 车辆速度优化

3.1.1 目标车速计算

在给定交通信号定时信息和车队领头车的位置信息后，可以计算得到车队中领头车的目标车速。为了保证交叉路口的通行效率，选取车辆可以在绿灯通过交叉路口的最大车速vi，h作为领头车的目标车速：

式中：vi，h(k)为k时刻车辆可以在绿灯通过交叉路口的速度上限；vi，l(k)为k时刻车辆可以在绿灯通过交叉路口的速度下限；d i，s(k)为k时刻车辆到信号灯的距离；tr和tg分别为红灯和绿灯时间间隔；tc为信号灯一个循环时间间隔；Kw为用于描述信号灯循环次数的整数。

3.1.2 随机模型预测控制

上层控制器旨在求解车队中智能网联汽车最优速度轨迹以降低整个车队燃油消耗，是一个带有多个约束的最优控制问题。考虑到驾驶员误差不确定性，本文中采用随机模型预测控制（SMPC）求解该最优控制问题［14-15］。

通过建立场景树模型作为随机模型预测控制输入，该模型包括从根节点到叶节点的所有不同路径。其中根节点定义为当前驾驶员误差的状态，叶节点定义为经过一段预测时域后驾驶员误差的状态。对于每一条可能的路径，其出现的概率可通过转移概率矩阵Te计算得到。图3为一个场景树例子，假设驾驶员误差状态的数量Ne为3，分别为e1、e2和e3，预测时域从t0到t4。已知t0时刻初始驾驶员误差为e2，则在下一时刻t1，驾驶员误差e1出现的概率为τ21，如图中红色箭头所示，可通过查询转移概率矩阵得到，以此类推可以计算后续时刻驾驶员误差出现概率，则该路径出现的概率为各个误差出现概率的乘积。由此根据场景树模型可以计算得到所有路径出现的概率值。

图3 场景树

上层控制器的优化目标为提升车队的燃油经济性，同时也考虑了交叉路口的通行效率和车辆乘坐舒适性。因此，SMPC的成本函数定义为车队单位距离油耗、车辆速度与目标车速平方差以及车辆加速度与目标加速度的平方差的期望之和。选取车辆的加速度作为SMPC的控制量和输出，其成本函数可表达为

式中：ω1、ω2和ω3为权重系数；T为预测时长；Nmc为路径数量；ps为路径出现的概率。

3.2 能量管理策略和效率反馈

下层控制器旨在优化混合动力汽车发动机和电池功率分配，从而进一步降低车辆燃油消耗。本文中采用自适应等效燃油消耗最小化策略（A⁃ECMS）来求解功率分配问题［16］。A⁃ECMS是一种被广泛使用的能量管理控制策略，能够适用于不同驾驶工况，具有较高的计算效率和精度。A⁃ECMS的成本函数可表达为

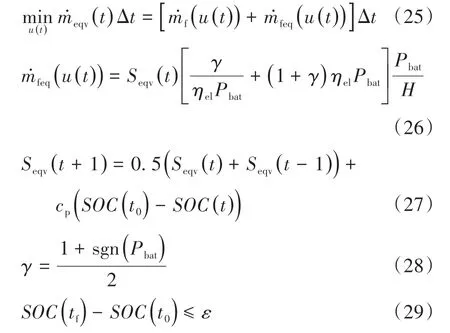
式中：(t)为等效燃油消耗率；Seqv(t)为等效系数；γ为单位阶跃函数；ηel为电路效率；ε为电池结束时间SOC值和初始时间SOC值差值的上限；cp为步长，作为比例反馈增益。

在上层控制器中，混合动力汽车的燃油消耗率计算与车辆的驱动和制动能量回收效率直接相关，考虑到上述两种效率会随车速变化而不断变化，因此，下层控制器需要定期计算车辆的驱动和制动能量回收效率并反馈给上层控制器，以修正上层控制器中车辆的燃油消耗模型。选取一定时间段内车辆的驱动和制动能量回收效率的平均值作为效率反馈值［10］：

式中：ηeff，ave和ηrec，ave为平均驱动和制动能量回收效率；Pe，in和Pe，out为发动机消耗和输出功率；Pm，in和Pm，out为电机输入和输出功率；Pbat，in和Pbat，out为电池充放电功率；ηg、ηf和ηw为变速器、主减速器和车轮的效率；Neff和Nrec为一定时间段内计算得到的驱动和制动能量回收效率的个数。

4 仿真结果与分析

4.1 仿真设置

在MATLAB/Simulink中建立混合动力汽车整车模型，如图4所示，其主要性能参数如表1所示。

图4 混合动力汽车整车模型

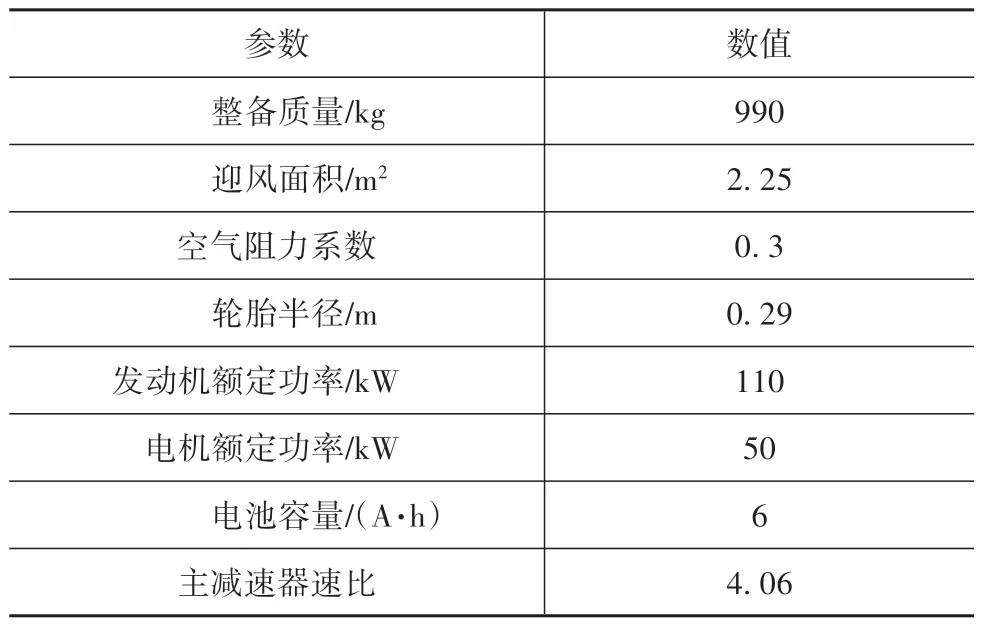
表1 混合动力汽车参数

仿真场景选取为单车道多个交叉路口，并考虑由4辆混合动力汽车组成的车队。信号灯红灯持续时间设置为30 s，绿灯持续时间设置为15 s，各交叉路口红灯初始时间随机生成。交叉路口数量设置为10，间隔500 m。道路允许最大车速设置为20 m/s，最小车速为0。车辆的最大加速度为3 m/s2，最大减速度设置为-6 m/s2。随机模型预测控制的优化性能与采样的路径数量相关，然而路径数量增加会导致算法计算效率变差。为提高算法的计算效率，采用蒙特卡罗算法［14］来生成一定数量的路径。图5为不同路径数量下算法单位步长的计算时间和车辆平均100 km油耗的仿真结果。可以看出增加路径数量并不一定能够降低车辆油耗，但是算法计算时间持续增加。综合考虑车辆油耗和算法计算效率，选取路径数量为100。

图5 不同路径数量下仿真结果

为了模拟真实的驾驶环境，仿真采用与文献［14］相同的驾驶员误差转移概率矩阵。该转移概率矩阵是由真实驾驶数据统计得到，将驾驶员误差状态划分为9级来近似表示实际驾驶员误差：-0.4，-0.3，-0.2，-0.1，0，0.1，0.2，0.3，0.4。值得注意的是，驾驶员误差分级和转移概率矩阵都是与驾驶员相关的，不同的驾驶员其误差分级与转移概率矩阵并不相同。本文所采用的转移概率矩阵如下：

为验证所提出的生态驾驶控制方法的可行性，本文中在不同车辆类型（网联汽车和传统人类驾驶汽车）组合下对算法进行仿真。将所提出的方法与另外两种基准方法进行比较。基准方法1，不存在驾驶员误差，采用模型预测控制（MPC）方法优化网联汽车速度轨迹；基准方法2，存在驾驶员误差，但是模型预测控制方法在优化网联汽车速度轨迹时不考虑驾驶员误差的影响。

4.2 不同队列组合下仿真验证

在所提出的混合动力汽车生态驾驶控制方法中，网联汽车与人类驾驶汽车组成队列行驶，车队领头车设置为网联汽车，而跟随车辆可以是网联汽车或者人类驾驶汽车。根据跟随车辆的类型不同，可以将车队划分成为3种不同的组合方式：跟随车辆全部为人类驾驶汽车、跟随车辆全部为网联汽车和跟随车辆为两种类型的混合。假设同一车队内的网联汽车驾驶员具有相同的驾驶风格，即采用相同的驾驶员误差模型，但是初始驾驶员误差不同。3种队列组合方式如图6所示，其中蓝色车辆为网联汽车，白色车辆为人类驾驶汽车。对于组合2，根据网联汽车位置和数量不同存在多种组合方式，本文中选取其中一种组合方式进行仿真验证。

图6 3种队列组合方式

4.2.1 组合1：跟随车辆全部为人类驾驶汽车

假设车队中领头车的初始驾驶员误差为-0.4 m/s2。图7为3种方法下车辆的速度轨迹仿真结果，由于基准方法1假设驾驶员不存在操纵误差，因此其仿真得到的车速轨迹为理想的最优轨迹。从图中可以看出，由于驾驶员误差的存在，使得基准方法2（不考虑驾驶员误差）下车辆的速度轨迹曲线明显地偏离最优轨迹曲线，这也导致后面跟随车辆的速度轨迹也发生偏离。而本文所提出方法（考虑驾驶员误差）下车辆的速度轨迹在有驾驶员误差存在的情况下，依然能够较好地跟随理想最优轨迹，且车速轨迹相比于基准方法2更加平滑。表2为3种方法下车辆100 km油耗。相比于不考虑驾驶员误差的基准方法2，本文所提出的方法可以有效降低车队的燃油消耗，平均油耗节约4.35%。由于车速轨迹并不能完全跟随理想最优轨迹，本文所提出的方法相比于基准方法1燃油经济性略差。

图7 队列组合1下的仿真结果

4.2.2 组合2：跟随车辆为两种类型的混合

当跟随车辆中有网联汽车时，假设前后网联汽车的初始驾驶员误差不同，分别是-0.4和0.2 m/s2。图8为3种方法下车辆的速度轨迹仿真结果，表3为3种方法下车辆100 km油耗。可以看出，本文所提出的方法相比于基准方法2，车辆速度轨迹更贴近理想最优轨迹，且车辆燃油经济性更好，油耗降低5.40%。另外，对比表2和表3中车辆的油耗，随着车队中网联汽车数量的增多，理想情况下，即没有驾驶员误差存在，车队的平均燃油消耗减少，这与网联率提升可以提高车队燃油经济性相符合。但基准方法2和本文所提出的方法下车队的燃油消耗反而略微增加了，主要原因是驾驶员误差在车队中具有传递性，前车的速度轨迹偏移会导致后面跟随车辆速度轨迹也发生偏移，增加跟随车辆的燃油消耗。

表3 队列组合2车辆100 km油耗 L

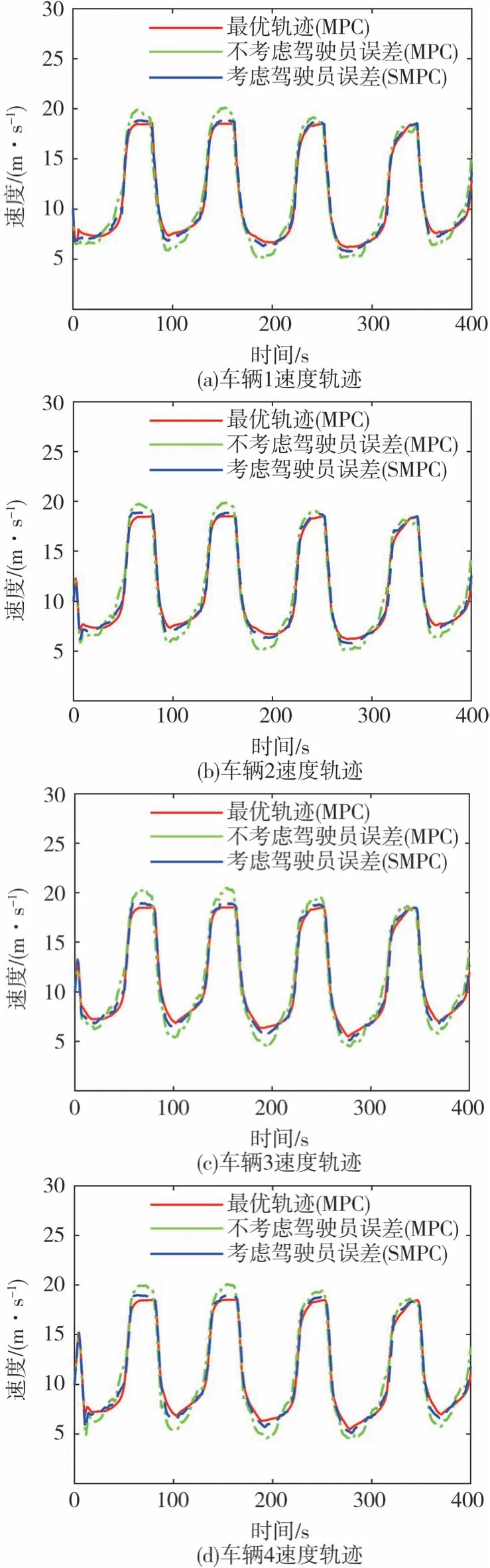
图8 队列组合2下的仿真结果

表2 队列组合1车辆100 km油耗 L

4.2.3 组合3：跟随车辆全部为网联汽车

当跟随车辆全部是网联汽车时，假设网联汽车的初始驾驶员误差分别为-0.4，-0.2，0.2和0.4 m/s2。图9为3种方法下车辆的速度轨迹仿真结果。

图9 队列组合3下的仿真结果

可以看出，尽管车队中所有车辆均为网联汽车，基准方法2下车辆速度轨迹相比于理想最优轨迹依然出现较大的偏移。本文所提出的方法相对减少速度轨迹的偏移量，但是相比于组合1和组合2，车辆的速度轨迹偏差较大。其主要原因在于车队中驾驶员误差数量的增加，导致系统的不确定性增强，且车队中前车的车速变化往往会对后车车速产生较大影响，本文所提出的算法旨在优化整个车队的燃油经济性，因此网联汽车特别是领头车，会为降低整个车队的燃油消耗做出一定的速度轨迹调整［3］，这也可能是网联汽车速度轨迹偏离最优轨迹的一个原因。表4为3种方法下车辆100 km油耗，本文所提出的方法相比于基准方法2，车辆燃油经济性提升2.82%。

表4 队列组合3车辆100 km油耗 L

5 结论

本文中以交叉路口混合动力汽车队列为研究对象，提出一种考虑驾驶员误差的分层生态驾驶控制架构，基于随机模型预测控制和自适应等效燃油消耗最小化策略分别设计上层控制器和下层控制器，并在3种不同队列组合方式下对算法进行仿真验证，仿真结果表明：

（1）在有驾驶员误差存在的情况下，相比于传统的模型预测控制方法，本文所提出的方法可以有效降低驾驶员误差对车队中混合动力汽车速度轨迹的偏移影响，使得车辆能够贴近最优速度轨迹行驶，从而提高车辆的燃油经济性；

（2）理想情况下，随着车队中网联汽车数量的增加，即网联率的提升，车队平均燃油消耗得到降低，但是当存在驾驶员误差时，由于驾驶员误差数量也随之增加，会降低网联技术对于车队的燃油经济性提升效果；

（3）减小算法的计算时间是生态驾驶控制方法实际应用必须考虑的因素，仍然需要进一步研究。