考虑投资者需要层次的投资组合三层规划模型

夏翘楚，胡 桥

（1.华南理工大学工商管理学院，广州 510640；2.广州市金融服务创新与风险管理研究基地，广州 510640；3.浙江大学计算机科学与技术学院，杭州 310027）

1 研究背景

在马科维茨1952年的工作中，投资者仅在收益-风险之间进行权衡［1］.然而，很多研究指出投资者面临的现实情境远比此复杂，因此一系列多目标优化研究应运而生［2-3］.新引入的目标可以简单分为财务类和非财务类，越来越多的学者引入社会责任作为第三个标准［4-5］，这可能来源于三个方面的原因：第一，越来越多投资者除了追求安全的未来，也想回馈社会［6］；第二，市面上有预先筛选好的社会责任共同基金可供选择，学者们可以借此机会调查相关基金公司是否真正将社会责任纳入考虑范畴［7］；第三，除了前述打包好的社会责任型基金，也可以从可持续性指数中抽取多个对象公司［8］，或者直接进行个体公司层次的研究：国际上已有独立评级机构对个体公司进行社会责任评价，以美国为例，有三家权威机构（Thomson Reuters、Bloom⁃berg和KLD）对众多上市美国企业进行了environmental，social and corporate governance（ESG）评级［9］.针对大部分A股上市公司，从2013年起，和讯网每年都会发布上市公司社会责任报告.基于五个一级指标（股东责任、员工责任、供应商、客户和消费者权益责任、环境责任和社会责任）的考虑，不仅给单个公司一个数字化的“总得分”（上限100），而且还对应分数段划分了字母等级.这些条件使得有关社会责任投资的研究具备必要性和可行性.

Bénabou和Tirole［10］指出投资社会责任表现好的公司的股票，这一行为受社会尊重和自尊的驱使.值得一提的是，这种心理活动与马斯洛需要层次理论中“尊重需要”不谋而合.Maslow［11］指出人类具有五个层次的需要，其中第四层“尊重需要”由外部尊重（主要指社会尊重）和内部尊重（主要指自尊）组成，目前已有部分投资组合研究直接基于该理论.在理论上，De Brouwer［12］对应五层需要分别给出合适的投资方式；马斯洛需要层次理论的核心在于人类的需要是逐层实现，而不是一次性得到满足的.因此在模型方面，Li等［13］提出了一个投资组合双层规划模型，考虑了投资者的安全需要和自我实现需要.在这个意义上，多层规划尤其适合这种框架.多层规划（包括双层和三层）用于求解多个分散化决策问题，且这些问题的决策变量处于一个层次化的整体中［14］，相比于双层规划，三层规划更加贴近现实场景［15］.除此之外，也有一些模型间接反映了人类的需要金字塔.在经典的行为投资组合理论（BPT）中［16］，带有两个心理账户的投资者用其第一个账户规避贫穷，第二个账户去追求财富.其中该理论通过一个非线性约束赋予第一个账户优先权.

然而一方面，现有基于马斯洛需要的研究多是只量化了安全需要和自我实现需要，极少有投资组合研究继续关注余下三层需要；另一方面，尽管社会责任投资被视为一种新的投资标准，但是几乎没有研究将其与尊重需要联系起来，也就更不会考虑其与传统二维指标的优先次序关系.因此，为了刻画安全需要、尊重需要和自我实现需要及其相互之间的关系，后文针对投资组合问题提出了一个三层规划模型，模型中，下层需要的目标是最小化风险，中层和上层则追求更高的社会绩效和财务收益.

同样还是在均值-方差模型中，Markowitz［1］假设投资者始终风险厌恶，但Friedman和Savage［17］发现，在现实生活中买保险的人也会买彩票，S型价值曲线表明投资者在面对收益和损失时具有不同的心态［18］.此外，BPT也隐含了投资者在下层账户风险厌恶，在上层账户却风险追寻的事实［19］.之后，通过调节收益、概率阈值的取值，独立的心理账户模型直接刻画了投资者变化的风险态度［20］.因此，为了更加全面地反映投资者的需要，独立的投资组合模型应该包含多个风险度量.已有一些学者从定义本身入手研究特定风险度量适合的心理状态，Dowd和Blake［21］、Dowd等［22］均指出，谱风险度量、CVaR和VaR分别适合风险厌恶、风险中性和风险追寻三种状态.本文模型在下层使用方差度量风险，中层和上层分别使用CVaR和VaR.

根据定义，VaR等风险度量的精确计算需要知道确切的收益分布［23］.为了提高计算效率，Ghaoui等［24］提出VaR的近似表达式.至于CVaR，通常需要先计算VaR，这类风险度量求解问题在多风险度量的模型中尤为突出［25］.为提高求解效率，后文将模型转化为半定规划求解器可以直接求解的形式.

风险度量是约束的一种特殊形式，事实上投资者会面临很多现实约束.比如频繁地买入卖出带来的交易费用会侵蚀收益［26］.因此很多研究考虑交易费用，徐永春［27］构建考虑非线性交易费用情形下的M-CVaR模型.杨兴雨等［28］提出了带交易费用的集成专家意见在线投资组合策略.目前，常用三种交易费用形式，包括比例型［29］、二次形式［30］和V型［31］.为了简单起见，假设交易成本与交易规模成比例.

总的来说，本文模型有以下四点创新：第一，针对投资组合问题构建三层次模型，反映了投资者的安全需要、尊重需要和自我实现需要以及这三种需要的实现顺序，这深化了马斯洛需要层次理论在投资组合领域的应用.第二，从内涵上将社会责任投资与尊重需要联系起来，为社会责任标准丰富了动机.第三，通过在每一层次使用不同的风险度量，捕捉了投资者随目标变化而变化的风险态度.第四，使用半定规划方法，优化了求解过程.

2 模型

2.1 假设与参数设定

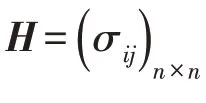
2.2 下层（安全需要）模型

对于投资者来说，任何投资的前提是该项投资不会影响他们的生活状况.换句话说，为了满足安全需要，他们需要保证初始财富安全.为了描述这种安全需要，假设投资者的目标是最小化投资组合的风险，并且鉴于方差衡量的是总体波动性，这一层使用方差作为风险度量.假设下层投资比例为z=( )z1,z2,…,zn′，则下层模型为：

其中：rl(z)=z′H z为投资组合的方差；G是投资者能够接受的最低收益率.式（3）是本层的预算约束，由交易成本和投资比例两部分构成［32］.

2.3 中层（尊重需要）模型

除了传统的财务绩效，通过社会责任投资，投资者收获社会满足感，这一行为部分由尊重需要驱使.为了避免不同基金公司对社会责任型基金的评价标准存在争议［4］，接下来使用公司层次的社会责任评价数据，由独立的评级机构提供.因此，为满足尊重需要，投资者希望所选投资组合表现出更好的社会绩效.假设θ=(θ1,θ2,…,θn)′为n种风险资产的社会责任报告的得分向量，为了将风险资产的得分划归0至1区间，对其进行如下标准化处理［33］：

参考Dorfleitner和Utz［34］关于社会责任评级的可加性.假设y=(y1,y2,…,yn)′为中层投资比例，则基于尊重需要的目标函数如下：

关于风险态度，一个广为接受的事实是投资者的绝对风险厌恶程度递减［22］.相比于下层安全需要，在追求中层尊重需要时，投资者的风险厌恶程度减弱.根据Dowd和Blake［21］，CVaR相比VaR适用的风险态度更显中性，因此本层使用CVaR度量风险.为了方便叙述，首先给出VaR定义，在此基础上定义CVaR.

定义1［35］设损失函数f(r)，r为随机收益率向量，给定置信水平α，Ψ(f(r),β)为损失不超过给定阈值β的概率函数，则VaR可定义为：

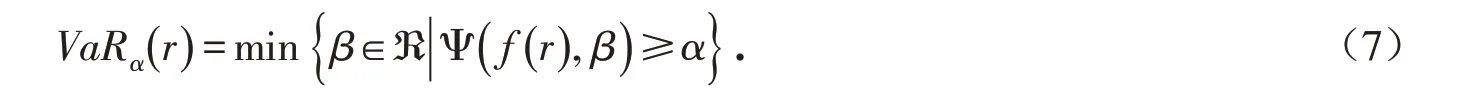
定义2［35］给定置信水平α，设随机收益向量r概率密度函数为π(r)，CVaR被定义为超过VaR的损失函数f(r)的期望值，即：

进一步地，中层CVaR约束可表达为（设其取值不超过L）：

注意到式（9）中含有VaR，但直到上层，模型才需要计算VaR.Rockafellar和Uryasev［36］提出了一个辅助函数并基于历史数据分散性近似取值，可以同时计算VaR和优化CVaR.因此，式（9）可以通过下式近似表达：

其中：历史收益率矩阵r∈ℝn×T已知.

此外，只有下层安全需要持续被满足，投资者才可能会关注中层尊重需要.通过如下方差约束建立两层之间的联系：

其中：rl(y)=y′H y为中层方差，f*=z′H z是下层安全需要的最优值.式（11）通过改变参数δ1的取值，控制安全需要的强度，除此之外，预算约束和卖空限制同样适用于本层.因此中层模型可以表达为：

2.4 上层（自我实现需要）模型

投资者在实现了上述两层需要之后，开始追求“自我实现”，表现为取得良好的投资绩效［12］.这意味着，上层目标函数可以表示为最大化投资组合的期望收益.由于上层输出最终投资比例，故上层的投资比例即为终端投资比例x=( )x1,x2,…,xn′.同时，投资者在上层的风险厌恶程度弱于中层，故上层使用VaR作为风险度量.需要注意的是，式（7）需要确切的分布信息.为了便于计算，借鉴Ghaoui［24］提出的VaR的实用表达式：

同样地，自我实现需要得到关注的前提是尊重需要持续被满足，因此通过引入下式，联系中层需要和上层需要.

2.5 三层规划模型

标记上层模型为Upper，中层模型为Middle，下层模型为Lower.完整呈现考虑投资者需要层次的投资组合三层规划模型：

3 求解

从第2章节可以看出，下层模型属于二次规划，对此MATLAB有直接的求解函数.中层模型和上层模型都含有一个锥约束，分别为式（11）和式（18）.对于此类约束，首先需要先转化为半定矩阵形式，然后以上层模型为例，继续重写VaR约束式（18），使其能够运用SDPT3包求解［37］.

3.1 锥约束形式的转化

首先，将中层模型中的方差约束（11）改写为标准的二阶锥形式：

其中矩阵C是协方差矩阵H的乔里斯基分解矩阵.进一步地，根据Lobo等［38］，二阶锥约束可以等价为一个半正定矩阵，则式（25）可以重写为：

其中In为n维单位矩阵.

同理，上层模型的VaR约束与以下半正定矩阵等价：

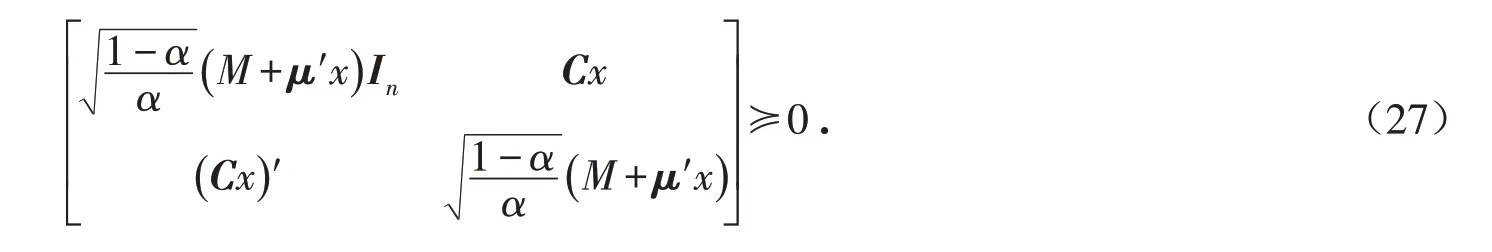
3.2 VaR约束的对偶半定规划形式

相比于半定规划的原问题，其对偶问题的决策变量是向量形式，因此更易求解，目前大量求解器直接求解对偶问题.简单起见，以上层模型为代表，根据Helmberg中式（2.3）［39］，按照如下标准对偶问题中约束的形式重写VaR约束：

其中：v∈ℝp是向量变量；Gi(v)代表第i个半定矩阵，i为约束的个数，Gi(v)可以写成决策变量分量vi的线性组合；Gi,k是第k个分量的系数矩阵，k从1开始，所有的Gi,k都必须是对称矩阵；Gi,0是常数项矩阵.

于是，首先定义向量形式的决策变量v为：

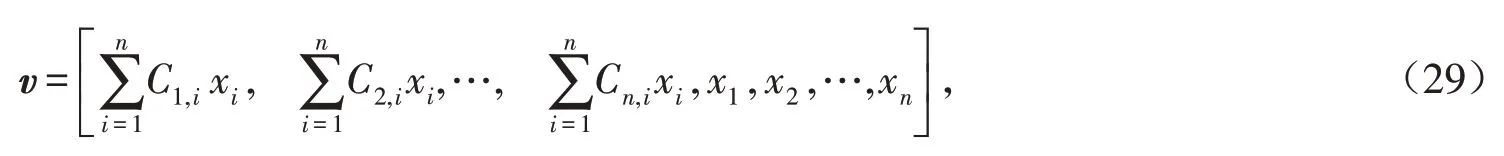
其中向量v的分量之间存在如下联系：

因此式（27）可进一步改写为：

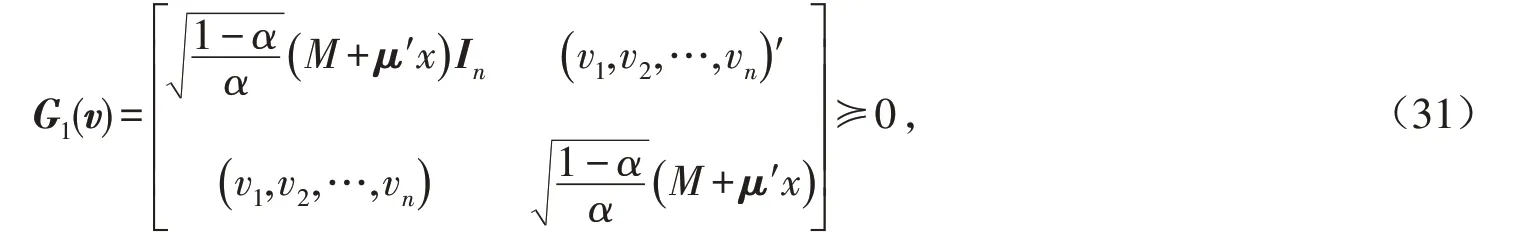
对应式（28），可得VaR约束的系数矩阵为：

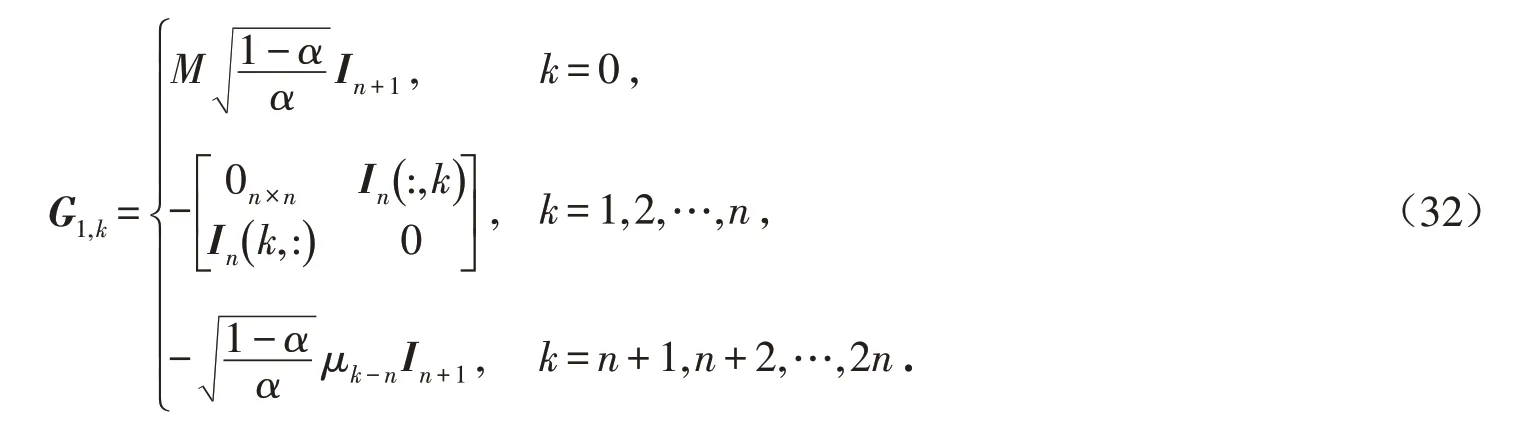
式中：In(: ,k)表示n维单位矩阵的第k列；In(k,:)为n维单位矩阵的第k行.

4 实证研究

为了说明模型的运用效果，利于A股市场数据进行实证研究.与此同时，对比相关模型的结果，包括：①追求安全需要的MV［1］，简记为“Safety”；②追求自我实现需要的M-CVaR［40］，简记为“Self-actu”；③分层次实现这两个需要的Variance-CVaR MPSM［13］，简记为“Maslow”.④等权重模型，简记为“EW”.

4.1 数据的选取

假设投资者从A股市场选择了30只股票，分布于10个行业，如表1.从锐思金融终端下载得到2014-01-01至2019-12-31收益率周数据（309周）.其中，2014-01-01至2018-12-31为样本内期间，余下的一年用来做样本外效果对比.此外，有关公司层次的社会责任评价，采用和讯网上市公司社会责任报告中的总得分（http://stockdata.stock.hexun.com/zrbg/Plate.aspx）.样本内期间30只股票的部分统计指标见表2.

表1 A股市场股票池Tab.1 Stock pool of A-share market

表2 所选30只股票的统计指标Tab.2 Statistical indicators of 30 selected stocks

4.2 样本内分析

约定相关参数的取值，包括：①简单起见，资产交易成本率ci统一设为0.001；②90%的置信水平；③下层可接受的最低周收益率G=0.05/52；④中层模型中，CVaR上限L=0.14；⑤上层模型中，VaR上限M=0.09，得分约束的调节参数δ2有两种取值，分别为0.06和0.07；⑥为了方便本文模型与Variance-CVaR MPSM模型对比，中层模型中的调节参数δ1的取值将与δ相同，均设为3E-04.为了方便之后研究δ2取值对最优结果的影响，做如下标记：当δ2=0.06时，本文模型记为“Tri*”；当δ2=0.07时，记为“Tri**”.表3为各模型运行后的结果.

表3 样本内不同模型的最优投资策略Tab.3 Optimal investment strategies of different models in the sample

表3结果显示，①投资资产的数量：Safety>Maslow=Tri*=Tri**>Self-actu，且Self-actu只投资于收益率均值最高的资产；②对于期望收益率排名前三的资产1、6、14，Maslow和本文模型均有一半以上的分配比例；③Tri*和Tri**均有共计超过30%的比例投资于得分排名前二的资产11、8.不难理解，以上的结果与各模型构建的动机一致.Safety为满足安全需要，尽可能分散化投资，而Self-actu则追求自我实现，仅投资高收益率资产，Maslow兼顾安全需要和自我实现需要，做到了折中.在Maslow的基础上，本文模型进一步考虑了社会责任得分，因此会投资社会责任得分高的资产.

4.3 样本外绩效

按照样本内的最优策略，样本外进行为期一年的投资.图1反映了累计收益率的变动情况.

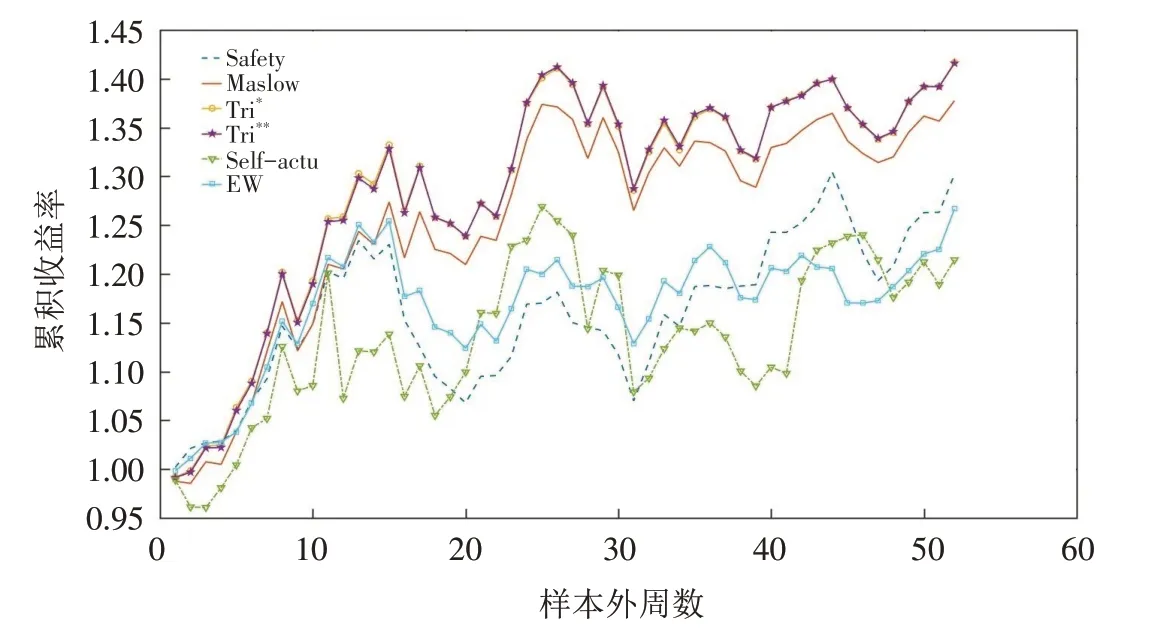
图1 样本外最优投资组合累积收益率Fig.1 Cumulative return rates of optimal portfolios out of the sample

由图1可以看出，①几乎在整个区间，Tri*和Tri**表现得最好，但这两条曲线几乎重合，这可能是因为上层模型的得分约束对最终实现收益率没有直接影响.②各组合期末收益率：Tri*>Tri**>Maslow>Safety>EW>Self-actu.

除了累积收益率对比，表4罗列了其他指标，包括：收益（R）、标准差（Std）、CVaR、VaR以及对应上述三个风险度量的单位风险报酬指标（R/Std、R/CVaR、R/VaR）、确定性等价（CE）以及组合的得分.

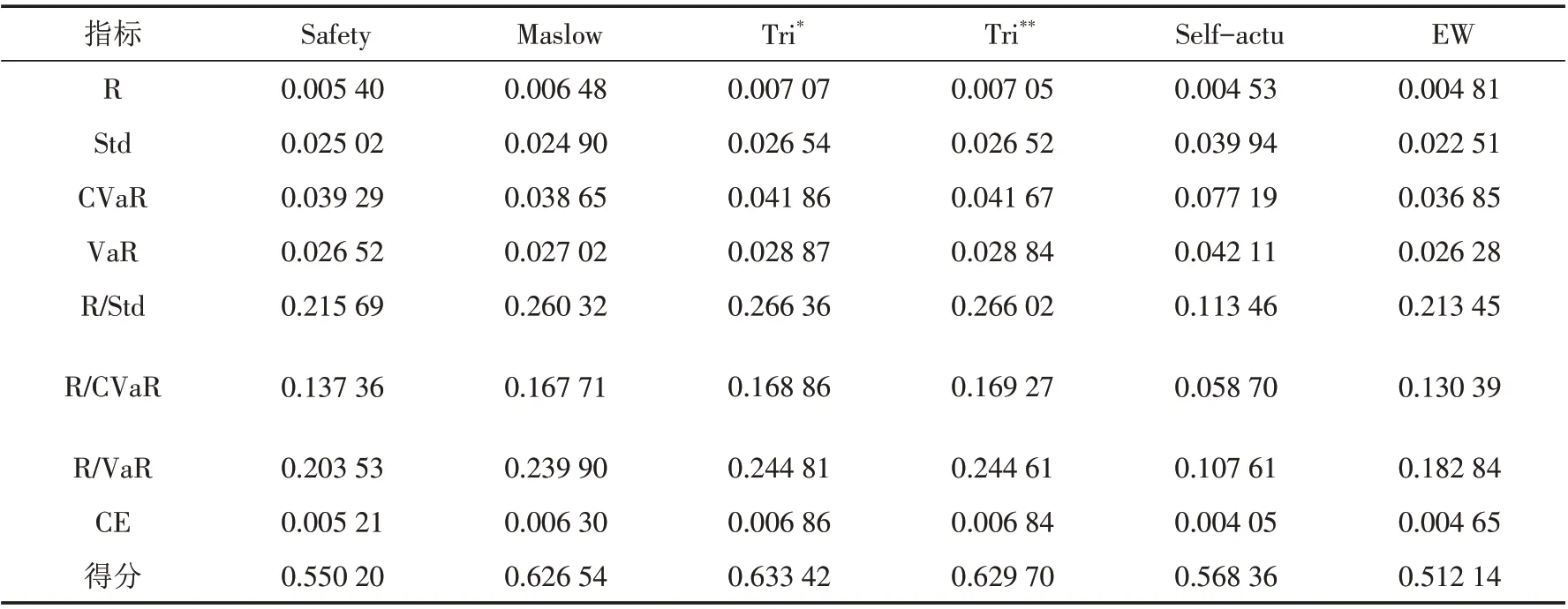
表4 样本外最优投资组合指标Tab.4 Investment result indicators of each model out of the sample

表4表明本文模型在大多方面优于相关模型：第一，从收益的角度看，本文模型在不同δ2取值下的结果均优于对比模型，而Self-actu策略的收益却是最低的.第二，本文模型的各类风险处于中间水平，分散化程度最高的EW策略风险最小，这些特征与模型动机是符合的.第三，三类风险度量调整后的收益反映了投资的效率，总体看来，Tri*和Tri**的表现较好.第四，CE可以间接反映投资者的效用偏好［41］，各模型的最优策略CE排名：Tri*>Tri**>Maslow>Safety>EW>Self-actu.另外有关社会责任绩效，本文模型也是最优的.

5 参数灵敏度分析

为了清楚最优投资策略是否受模型某些参数的影响以及这种影响是否符合预期.接下来仅针对上层模型中得分约束的调节参数(δ2)和VaR约束的上限（M）进行分析.之所以只考虑上层模型，是因为上层对最终优化结果产生更加直接的影响.图2展示了这两个参数对模型相关指标的影响.

5.1 调节参数δ2的灵敏度分析

由前述分析可知，在上层δ2是关于投资组合得分约束的调节参数，因此接下来仅分析δ2对最优投资策略得分的影响.δ2从0.03开始，固定步长0.01，取六个值，相应的最终得分如图2 a，图中显示随着δ2的增大，投资组合得分随之降低，这与对应的得分约束逻辑一致.

图2 样本外上层参数灵敏度分析Fig.2 Sensitivity analysis of upper-level parameters out of the sample

5.2 约束上限M的灵敏度分析

不同于上述调节参数，作为风险度量约束的上限，M的取值必须限定在合理范围内，一方面，为了使得最优解存在，在其他条件不变的前提下，根据历史表现，要求M不能小于0.085；另一方面，为了保证约束效力，要求M不能大于0.11.因此，针对M，取如下六个值，间隔0.005.图2（b）展示了样本外VaR相关指标随VaR上限取值M变化的情况.同样地，无论是VaR随着M的增大而增大，还是R/VaR随着M的增大而减小，都是符合模型预期的.

6 结论

本文基于马斯洛需要层次理论，依次量化投资者的安全需要、尊重需要和自我实现需要，分别对应最小化风险、最大化社会责任评分和最大化期望收益三个目标，以此建立投资组合三层规划模型.模型在所有层次均考虑比例型交易成本，并在每一层使用不同风险度量，以刻画投资者随目标变化的风险态度.然后，使用求解器SDPT3求解模型，并基于A股数据对比相关模型.最后，对部分参数进行灵敏度分析.结果表明，在传统双目标的基础上引入社会责任评分可帮助投资者获得更高的财务收益和社会效用.若投资者降低对于尊重需要的要求，投资组合的社会责任评分会减小；若投资者愿意接受更大风险，投资组合的风险相应增大，单位风险报酬减小.