一类双变量几何概型题的探究
中山市桂山中学(528463)蔡晓波
几何概型中的双变量类型的题目是学生学习的一个难点,本文以人教版必修3 第142 页[1]的一道习题为例对其进行变式探究.
一、课本题目与解答
题目甲乙两艘轮船都要在某个泊位停靠6 个小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少一艘在停靠泊位时必须等待的概率.
分析1甲乙两艘轮船均是随机到达,故将甲乙两艘船到达时间分别视作x,y,故问题转化为仅需根据题意列出x,y的约束条件和题目要求的关于x,y的目标不等式即可求解.
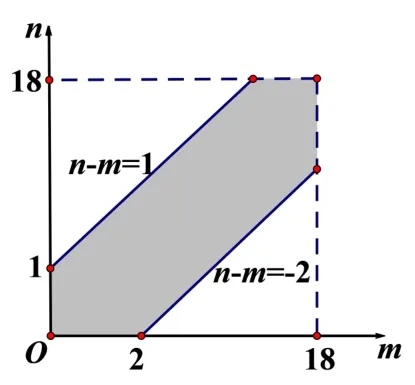
解法1设甲到达泊位的时间为x,乙到达泊位的时间为y,依题意可得:而这两艘船中至少一艘在停靠泊位时必须等待等价于|x−y|<6,即−6 图1 分析2此题有2 个变量,故我们可用主元的思想来达到降低变量的个数,这两艘船中至少一艘在停靠泊位时必须等待实际上包含2 种情况:①乙船先到且甲必须等待;②甲船先于或者同于乙船到达且乙必须等待.且由对称性可知这2 种情况概率相等,故仅需分析其中一种情况即可.古典概型中,我们可以把满足要求的情况相加除以总情况得出,而几何概型是连续不断的,而积分正好是用于“连续不断相加”的有力工具,故可以结合积分来解决该问题. 解法2设故这两艘船中至少一艘在停靠泊位时必须等待的概率为P,乙船先到且甲必须等待的概率为P1 根据甲乙到达时间的对称性可得P=2P1,设甲到达泊位的时间为x,乙到达泊位的时间为m,故0 ≤x <24,0 ≤m<24,当0 ≤m≤18 时,则x∈[m,m+6)时必须等待,此时甲需等待的概率为当18 此题既考查了学生的几何概型的知识又考查了学生的数学建模的能力和线性规划的相关知识,有一定的综合性,故对于初学者有一定难度.笔者对此题做了如下的变式探究,供同行参考,望批评指正. 约定:在下列解题过程中,均设甲到达泊位的时间为x,乙到达泊位的时间为y. 思考1课本的题目是已知停靠时长,求概率,那么如果知道概率能否求时长呢?为了方便理解,我们对概率赋予特定的已知值得到如下变式: 变式1甲乙两艘轮船都要在某个泊位停靠m(0 图2 图3 根据变式2 可知满足要求的m,n在以(24,24)为圆心半径为24 的圆的外部,且在边长为24 的正方形的内部,故本变式可以进一步做如下变式: 思考2课本的题目规定了甲乙两艘轮船都在同一昼夜的时间段中随机到达,且停靠时间相同,那么如果两艘船到达的时间段不同或者停靠时间均不相同又该怎么解呢?如果已知等待的概率,对于两艘船到达的时间段与停靠时长又有何要求呢?笔者对以上问题做了探究,为了方便理解,我们均对已知条件相关数据赋予特殊值,得到如下变式: 变式4甲乙两艘轮船都要在某个泊位停靠,甲需要停靠2 小时,乙需要停靠1 小时,假定甲船在凌晨8 点到下午14 点之间随机到达,乙船在同一昼夜的凌晨9 点到下午15点之间随机到达,求这两艘船中至少一艘在停靠泊位时必须等待的概率. 图4 图5 一个自然的问题是:如果甲乙当中一艘船可能到达的时间段固定,另一艘船可能到达的时间段不固定,那么两艘船中至少一艘在停靠泊位时必须等待的概率随着另一艘船到达时间段的改变有何变化呢?基于以上思考,可得如下变式: 变式5甲乙两艘轮船都要在某个泊位停靠,甲需要停靠2 小时,乙需要停靠1 小时,假定甲船在凌晨8 点到下午14 点之间随机到达,乙船在同一昼夜的24 小时内的时间段[m,m+6)(0 ≤m<18)内随机到达,求这两艘船中至少一艘在停靠泊位时必须等待的概率的取值范围. 图6 图7 图8 图9 图10 图11 注在本变式中,甲船与乙船可能到达的时间段长度均为6,此时x,y的总情况在坐标轴中恰为一个正方形,因此使得对m分类情况不会过多.此外,通过改变甲船和乙船的等待时间亦可增加或者减少分类情况,读者可以通过修改值和甲乙两船等待时间去体验一下. 变式6甲乙两艘轮船都要在某个泊位停靠,甲需要停靠2 小时,乙需要停靠1 小时,假定甲船在24 小时内的时间段[n,n+6)(0 ≤n <18)内随机到达,乙船在同一昼夜24小时内的时间段[m,m+6)(0 ≤m <18)内随机到达,已知这两艘船中至少一艘在停靠泊位时必须等待的概率不超过,求m,n必须满足的条件. 分析此时x,y的总情况为:是一个会“动”的正方形,且边长均为6,故可以利用变式5 的结论来解决本变式. 解题意可得是一个边长均为6 的正方形,设为正方形ABCD,且四点坐标分别为:A(n,m),B(n+6,m),C(n+6,m+6),D(n,m+6),而这两艘船中至少一艘在停靠泊位时必须等待必须满足:0 ≤y−x<2 或0 由变式5 可知ABCD与区域Q共有7 种位置关系.设这两艘船中至少一艘在停靠泊位时必须等待的概率为P,故由变式5 可得当点A,C恰好落在直线x−y+2=0 或者x−y−1=0 上时,当点A,C在直线x−y−1=0下方或者点A,C在直线x−y+2=0 上方时.注意到AC的斜率与直线x−y+2=0 和x−y−1=0 斜率相同,故仅需保证点A不在直线x−y−1=0 上方或者点A不在直线x−y+2=0 下方时即可,故n−m−1 ≥0 或n−m+2 ≤0,即n−m≤−2 或n−m≥1. 变式7甲乙两艘轮船都要在某个泊位停靠,甲需要停靠2 小时,乙需要停靠1 小时,假定甲乙两船均在同一昼夜中某一时段长为6 小时的连续时间段内随机到达,求这两艘船中至少一艘在停靠泊位时必须等待的概率不超过的可能性. 图12 图13 课本中此题为应用题,故我们不禁思考能否通过改变该题的问题背景来进一步考察学生呢,因此我们有如下变式: 变式8A,B两地有且仅有1 条河,甲船在A地,乙船在B地,甲船和乙船在同一昼夜内随机出发,且速度相同,并且都能够在6 个小时内走完全程,求甲乙两船途中相遇的概率. 解设甲出发的时间为x,乙出发的时间为y则要使甲乙两船途中相遇,则必须满足两艘船出发时间间隔不超过6 小时即可,故:|x−y| <6,故此题与本文开头所探究的课本题目一样,接下来的解法见本文开头课本题目解法1.至此,我们对课本的这道几何概型题目进行了系统的变式探究,每类变式均循序渐进,由易到难,由“静”到“动”. 教学中,要深入研究,挖掘出题目背后隐含的深刻含义以及丰富的变式形式;通过对题目进行各类变形来训练学生,既能达到以“变”应变的效果,又能让学生深刻体会到数学的美与数学的严密性.
二、题目变式
(一)两船停靠时长的变式探究


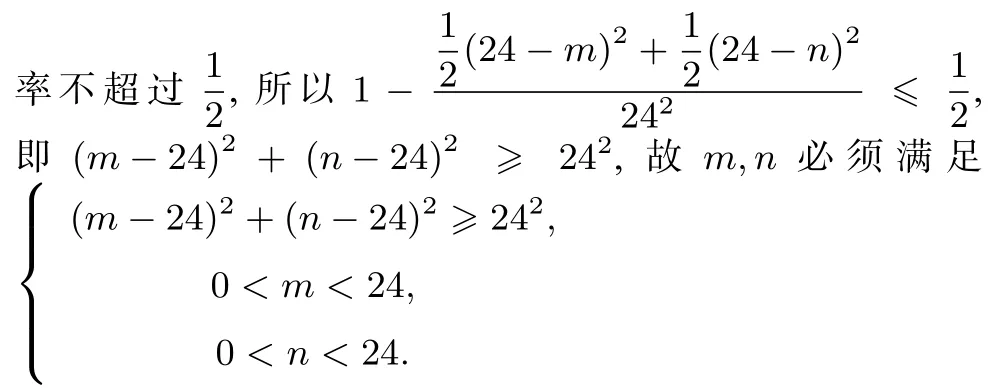



(二)到达时段的变式探究


















(三)题目背景变式

