基于跳扩散模型对随机利率下远期开始期权定价研究

孙彩灵, 刘丽霞

(河北师范大学 数学科学学院, 石家庄 050024)

0 引 言

随着经济的不断发展，金融衍生品受到了越来越多衍生品交易者的青睐。因此,期权的定价问题也引起了学术界和业界的高度关注。19世纪70年代，Black和Scholes提出了期权定价的B-S模型[1]。B-S模型中假设利率是常数，资产价格服从几何布朗运动。为了使B-S模型的适用范围更广泛，有必要对B-S模型进行扩展。一方面，由于实际生活中的利率是随机波动的，许多学者对随机利率下期权的定价进行了研究，例如，2008年，李淑锦等研究了随机利率下复合期权和重置期权的定价[2]；2015年，韩松研究了随机利率下亚式期权定价的新方法[3]；2021年，史言研究了随机利率混合指数跳扩散模型下的期权定价[4].考虑到CIR和Vasicek两种利率模型中， Vasicek利率模型的均值回归性更加符合实际，因此,本文假设利率服从扩展的Vasicek模型。另一方面，考虑到突发事件可能会发生，如政府政策的变化、自然灾害等，这些都将对金融市场有很大的影响，导致资产价格发生突然的跳动，因此，在模型中加入刻画资产价格波动的复合泊松过程，能使模型更加切合实际。如2004年，钱晓松研究了跳扩散模型下交换期权的定价[5]；2012年, 李翠香等研究了基于随机利率下跳-扩散过程的复合期权定价公式[6]；2018年，李艺卓等研究了跳扩散模型下的二选期权定价等[7]；2021年，刘朝晖等研究了跳扩散模型下交换期权定价的Mellin变换方法[8]。

近年来，金融市场交易了大量的奇异期权，如复合期权、障碍期权和彩虹期权等。远期开始期权是以在事先约定未来某一时刻开始生效，且执行价格为期权生效时刻的标的资产价格的路径依赖期权[9]。期权生效时刻为，到期日为，执行价格为S(T1)的欧式看涨和看跌远期开始期权在到期日的收益分别为

c(T,S(T))=max(S(T)-S(T1),0)

p(T,S(T))=max(S(T1)-S(T),0)

迄今为止，有很多关于远期开始期权的定价研究。2012年，王献东给出了基于Egarch模型的远期开始期权定价[10]；2018年，孙慧等给出了带信用风险的远期起点期权的定价[11]；2020年，李翠香等研究了基于NIG模型的远期开始期权的定价[12]。为了丰富远期开始期权的研究，本文将假设股票价格服从跳扩散模型，并且其收益率和波动率服从关于时间的非随机函数，在扩展的Vasicek利率模型下，利用跳扩散模型下的Girsanov定理和测度变换的方法推导欧式看涨和看跌远期开始期权的定价公式。

1 预备知识和引理

以下设(W,F, {Ft},Q)为带有域流{Ft}的概率测度空间，其中Ω为样本集合，F为Ω生成的σ域，Q为风险中性测度, {Ft}为本文所涉及到的随机过程所生成的域流。并且假设资产价格S(t)服从如下随机微分方程(以下记为SDE(1)):

(1)

无风险利率r(t)服从扩展的Vasicek利率模型(以下记为SDE(2))：

dr(t)=(θt-atr(t))dt+σr(t)dZ(t)

(2)

式中S(t-)表示左极限，为了书写简便，下面将S(t-)记为S(t)。W(t)和Z(t)为测度Q下的标准布朗运动，且相关系数为ρ。N(t)为到达参数为λ且独立于W(t)和Z(t)的泊松过程。Uj(j=1,2,…)表示资产第j次跳跃的跳跃幅度，且Uj为独立同分布的随机变量序列，且当j≥1时，Uj服从对数正态分布，即

下面介绍几个重要引理：

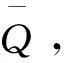
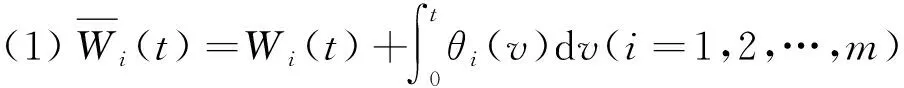
引理1.3[2]假设随机利率r(t)服从SDE(2)，则

(3)

基于引理1.1满足的条件，运用鞅方法也可以获得贴现债券的价格，因此有以下引理。

引理1.4[2]当利率满足SDE(2)时，到期日为T的贴现债券t时刻的价格B(t,T)满足

(4)

引理1.5假设资产价格S(t)服从SDE(1)，则有以下表达式:

(5)

2 随机利率跳扩散模型下远期开始期权的定价

定理2.1设标的资产S(t)服从SDE(1)，利率r(t)服从SDE(2)，则生效日为T1，到期日为T，执行价格为S(T1)的欧式看涨远期开始期权在0时刻的价格为：

式中N(·)表示标准正态随机变量的累积分布函数，且

证明

由风险中性定价原理可得:

(6)

首先计算I1。取

(7)

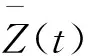
那么

从而在Q1下，Uj的密度函数为:

进而可以得到Q1下，lnUj的密度函数为：

由引理1.1可得:

I1=EQ[Λ1(T)S(0)I{S(T)>S(T1)}]=S(0)EQ1[I{S(T)>S(T1)}]

(8)

将式(7)代入式(5)，得:

(9)

将式(7)代入式(3)，得:

(10)

结合式(4)、式(9)和式(10)可得资产价格在Q1下服从的方程为:

(11)

由式(11)可得:

由式(8)可得:

EQ1[I{S(T)>S(T1)}|N(τ)=n]

=N(d1)

(12)

由式(8)和式(12)可得:

(13)

下面计算I2。取

式中，

由引理1.2可得, 在新测度Q2下，有:

(14)

(15)

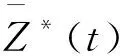
由引理1.1可得:

I2=S(0)EQ[H(0,T1,T)Λ2(T)I{S(T)>S(T1)}]

(16)

由引理1.3和引理1.4可得，资产价格S(T)在Q2下的方程为：

(17)

由式(17)可得:

由式(16)可得:

EQ2[I{S(T)>S(T1)}|N(τ)=n]

=N(d1-m(T1,T,n))

=N(d2)

(18)

由式(16)和式(18)可得:

(19)

I2得证。

结合式(13)和式(19)，定理2.1得证。

推论2.1在定理2.1的条件下，欧式看跌远期开始期权在0时刻的价格为:

证明：类似定理2.1可证。

3 数值实验

在上述分析中，分别得到了远期开始看涨和看跌期权的定价公式。本部分将利用Matlab软件分别给出各参数对期权价格的影响。为了便于计算，以下假设关于时间的确定函数θt、σr(t)、σ(t)和at均为常数，分别记为θ、σr、σ、a，且各参数对应的值如表1所示。

表1 相关参数值

在以上参数假设的基础上，利用Matlab软件作图，分别得到了变量T、a、μ、λ、θ和σr的变化对期权价格的影响，如图1～图6所示。

图1中曲线1给出了随机利率跳扩散环境下远期开始看涨期权的价格随时间变化的图像，曲线2表示普通欧式远期开始看涨期权的价格随时间变化的图像，通过对比可得，随机利率跳扩散环境下的期权价格远比普通期权价格高，因此，研究随机利率跳扩散环境下的期权定价更具有现实意义。

图2～图4分别表示变量a、μ和λ对随机利率跳扩散模型下远期开始看涨期权的价格影响，由图像可得，期权价格随a、μ和λ的增大而增大，随θ和σr的增大而减小。

图5和图6分别表示变量θ和σr对随机利率跳扩散模型下远期开始看涨期权的价格影响，由图像可得，期权价格随θ和σr的增大而减小。

图1 远期开始看涨期权价格图像

图3 期权价格与μ的关系

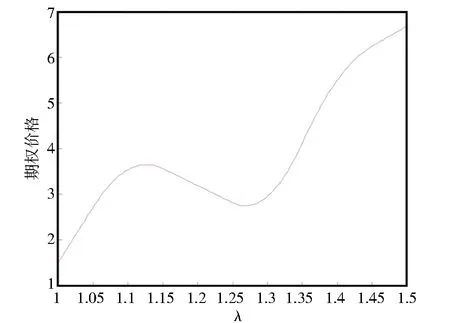
图4 期权价格与λ的关系

图5 期权价格与θ的关系

4 总 结

首先假设资产价格服从跳扩散模型下的几何布朗运动，且无风险利率服从扩展的Vasicek利率模型，模型中的布朗运动相关系数为ρ。其次利用跳扩散模型下的Girsanov定理和测度变换的方法得到欧式看涨和看跌远期开始期权的定价公式。最后通过数据分析得到随机利率跳扩散模型下远期开始看涨期权价格比普通远期开始看涨期权价格高，并分析了各个变量对期权价格的影响。