反演量子位势支集的多水平采样算法

常宝晶, 李 媛,2

(1.黑龙江大学 数学科学学院, 哈尔滨 150080;2.黑龙江大学 黑龙江省复杂系统与计算重点实验室, 哈尔滨 150080)

0 引 言

随着现代科技的发展，反演技术已成为研究各种科学和工程技术问题的重要手段[1-2]。反散射理论与方法广泛应用于遥感、无损探测、地球物理、医用成像和雷达目标识别等方面[3-6]。反问题一般具有不适定和非线性的特征，数值算法实现比较困难。目前量子反散射的研究主要集中在理论方面[7-8], 而量子应用领域急需从计算的角度来重构有效的数值算法。近年来，声学和电磁学反散射领域的算法和技术飞速发展，这也为量子反散射问题的研究带来了启发。如文献[9]将声学反散射中的因子分解法[10]推广到了Schrödinger方程情形，利用该方法反演位势支集。

在反散射问题中，为了反演散射体的位置，通常需要预先定位一些包含所有散射体的近似域。否则，将不得不使用一个比散射体实际尺寸大得多的近似域，而这样就会导致大量额外的计算。人们常采用抽样类算法来反演散射体的形状，如线性抽样法[11-12]、直接抽样法[13]和推广的线性抽样法[14-15]。文献[16]提出了一种多水平线性采样算法，该方法的优点是降低了原始线性采样法的计算成本。文献[17]构造了反演非均匀介质所占区域的多水平采样算法，该算法比直接抽样法收敛速度快，可以很容易地分离出多个不相交的散射部分，只需几次迭代就能找到每个部分比较满意的初始位置。受到文献[17]的启发，本文考虑将多水平采样算法应用于定态Schrödinger方程的位势反散射问题中，用来反演Schrödinger方程中位势的支集。

考虑如下定态Schrödinger方程：

(-Δ+q(x)-k2)u(x)=0，x∈Rn

(1)

式中:Δ代表Laplace算符；q(x)代表位势；通常称k2为能量，其中k∈R为波数，k=2π/λ，λ表示波长；空间维数n=2，3。设入射平面波

ui=eikx·d

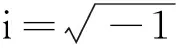
u=ui+us

(2)

式中总场u满足Schrödinger方程(1)，并且散射场us在无穷远处一致满足Sommerfeld有界条件和辐射条件：

(3)

称上述的模型问题(1)～(3)为正散射问题。对于正散射问题可描述为：给定波数k、位势q(x)、入射场ui, 当散射场us满足(3)时，求方程(1)和(2)的解u或us。

反散射问题有多种提法[18-19]，本文的提法是利用散射场的近场数据反演位势支集，即：假设位势q(x)具紧支集Ω，给定波数k及几个入射方向，通过测量的散射场来反演q(x)的支集。在这类反散射问题中，需要确定散射体Ω中任意点x的位势q(x)的近似值，从而近似确定散射体的形状和位置。

对于每个入射场ui(x)，总场u(x)满足Lippmann-Schwinger方程[20]：

(4)

式中

(5)

式中us(x)在S上测量，S为Rn中半径为R的圆周(当n=2时)或球面(当n=3时)。

令w=q(x)u(x)，x∈D，将其分别代入式(4)和式(5)中,可得:

w=q(x)ui-q(x)(GDw)(x),x∈D

(6)

和

us(x)=-(GSw)(x),x∈S

(7)

式中D为包含支集Ω的一个抽样域，积分算子GD和GS的定义如下

方程(6)和方程(7)将是提出的多水平采样算法的两个基本方程。

1 反向传播函数

称其为反向传播子空间。

设wb为方程(7)在空间Vb上的最佳逼近解，即：

(8)

上式的变分形式为：

Re(us+GSwb，GSvb)L2(S)=0， ∀vb∈Vb

(9)

或等价地

(10)

由于wb,vb∈Vb，则令

(11)

式中λ和μ为实常数。将式(11)代入式(10)，解得：

(12)

从而

(13)

称wb为反向传播函数。

2 多水平采样算法

(14)

通过最小化状态方程(6)所对应的残差方程来近似x点的位势q(x)，即求：

(15)

通过计算，可得式(15)的极小值点q(x)有如下表达式：

(16)

式中Re表示取复数的实部，横线表示复共轭。对每个抽样点x，计算q(x)。理论上，若q(x)≠0，则x在q(x)的支集Ω内；若q(x)=0，则x在Ω外。显然式(14)和式(16)的计算相对粗糙，即对w和q的近似误差较大。但与多水平采样算法相结合，就可以比较高效的近似定位位势支集的位置及形状。

为了描述多水平采样算法，首先引入两个概念，即“最小距离”和“具有指标M的第一个间隙区间”。给定有限的非减序列{q1,q2,…,qm}，将序列中全部相邻的元素作差，用dist(qi,qi+1),i=1,2,…,m-1来表示，找出最小的正的差值，称该差值为“最小距离”。对于所有的m-1个距离，假如存在j，使得2≤j≤m-1，且距离dist(qj,qj+1)至少是序列{q1,q2,…,qj}的最小距离的M倍，则称(qj,qj+1)为一个“间隙区间”，称第一个这样的“间隙区间”为“具有指标M的第一个间隙区间”。

多水平采样算法描述如下:

(1) 选择一个抽样域D，使其包含散射体Ω。在D上选择一个均匀(粗糙的)网格，由正方形(2D)或立方体(3D)组成，将该网格记为D0。选择一个误差ε和指标M，并设初始阈值c0=0和k=1。

(2) 对于任意的网格点x∈Dk-1，利用公式(14)和(16)计算q(x)的近似值。然后执行下面的步骤：

(i) 将满足qk(x)≥ck-1的qk的值按递增顺序进行排序，在这个序列中找到具有指标M的第一个间隙区间。选择这个区间的右端点作为下一次迭代的阈值ck。

(ii) 如果某个网格点x处的值qk(x)≥ck，则选择所有以此x为顶点的网格点，更新Dk-1为所有选中的网格点，并删除Dk-1中未被选择的所有网格点。

(3) 如果|ck-ck-1|≤ε，设Dk=Dk-1并执行步骤(4)。否则，加细Dk-1中的网格并记为Dk，设k=k+1，回到步骤(2)。

(4) 输出所有Dk中的网格点来确定位势的支集。

3 数值实验

式中C为Euler常数，用该式中前四项的和近似G(x,y)。在以下所有的实验中，取第一次迭代中的第一间隙区间指标M=1016，在剩余的迭代次数中均取M=100。在第一次迭代中选取很大的指标的原因是为了快速剔除抽样域中距离支集较远的区域。反演的图形中红色曲线代表精确支集的边界，黑色网格线构成的区域代表反演的位势支集的近似。网格加细基于简单的二分法，将网格进行二等分，即将每个正方形元素划分为四个面积相等的子正方形。

例1取位势支集Ω为以原点为中心、边长为0.3λ的正方形。在Ω内q(x)≡2。取抽样域D=[-1.2λ,1.2λ]×[-1.2λ,1.2λ]。

图1 一次迭代反演的结果

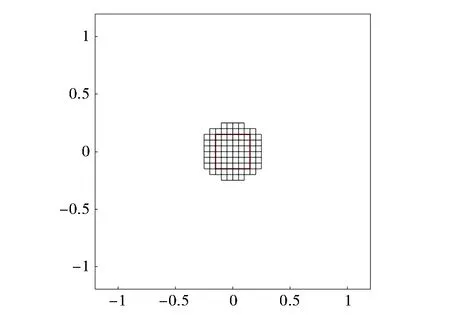
图3 四次迭代反演的结果

图4 五次迭代反演的结果

图1～图4分别为例1情形下第一、三、四和五次迭代后的数值实验结果。从图中看出，该算法的收敛速度非常快，经过五次迭代就能近似定位位势支集的位置及大概的形状。为了更清晰地展现迭代过程，在表1中给出了每次迭代开始时的网格点数目，通过该次迭代去掉、保留和再生的网格数目，以及迭代结束时的网格点数目。可以看到，第三次迭代中出现了6个再生网格点，这说明该算法具有自适应的特点，可以自动调整之前迭代的结果。

例2取位势支集Ω包含两个边长为0.3λ的正方形，中心点分别为(-0.3λ,-0.3λ)和(0.3λ,0.3λ)。在Ω内，

取抽样域D=[-1.2λ,1.2λ]×[-1.2λ,1.2λ]。

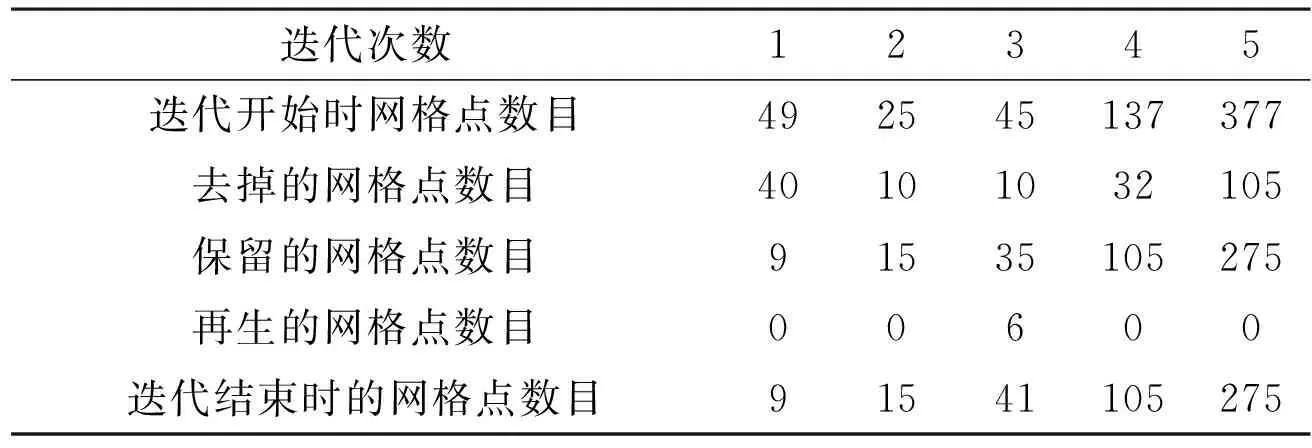
表1 各次迭代的网格点信息

图5 第一次迭代反演的结果

图7 第三次迭代反演的结果

图8 第四次迭代反演的结果

图5～图8分别为例2情形下前四次迭代后的数值实验结果。与例1相比，例2中需反演两个不相交的正方形。可以看出，经过四次迭代就能较满意地近似出每个散射体的初始位置，而且还能快速将两个不相交的部分分离。表2给出了各次迭代对应的网格点信息，仍然可以看到该算法的自适应特征。

例3取位势支集Ω为由半径0.3λ和0.5λ的圆围成的圆环，两个圆均以坐标原点为中心。在Ω内，q(x)≡2。取抽样域D=[-2.8λ,2.8λ]×[-2.8λ,2.8λ]。

在例3中，要近似反演一个半径为0.2λ的细圆环，抽样域D约为圆环面积的62倍。前四次迭代的反演结果如图9～图12所示。与例1和例2相比，反演的图形不再是正多边形，但与例1和例2一样，经过几次迭代，该算法依旧能反演出比较满意的结果。相应的网格点信息如表3所示。可以得出与例1和例2类似的结论。

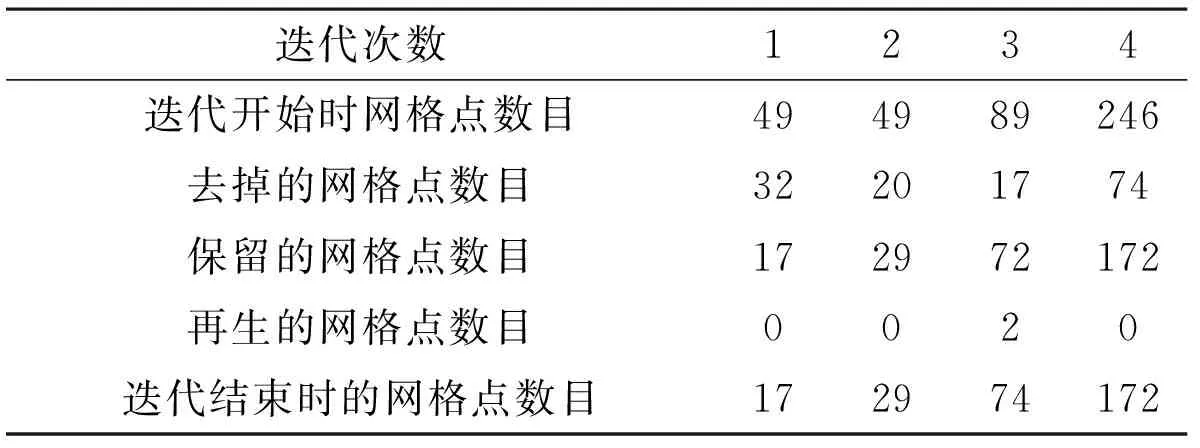
表2 各次迭代网格点信息

图9 第一次迭代反演的结果

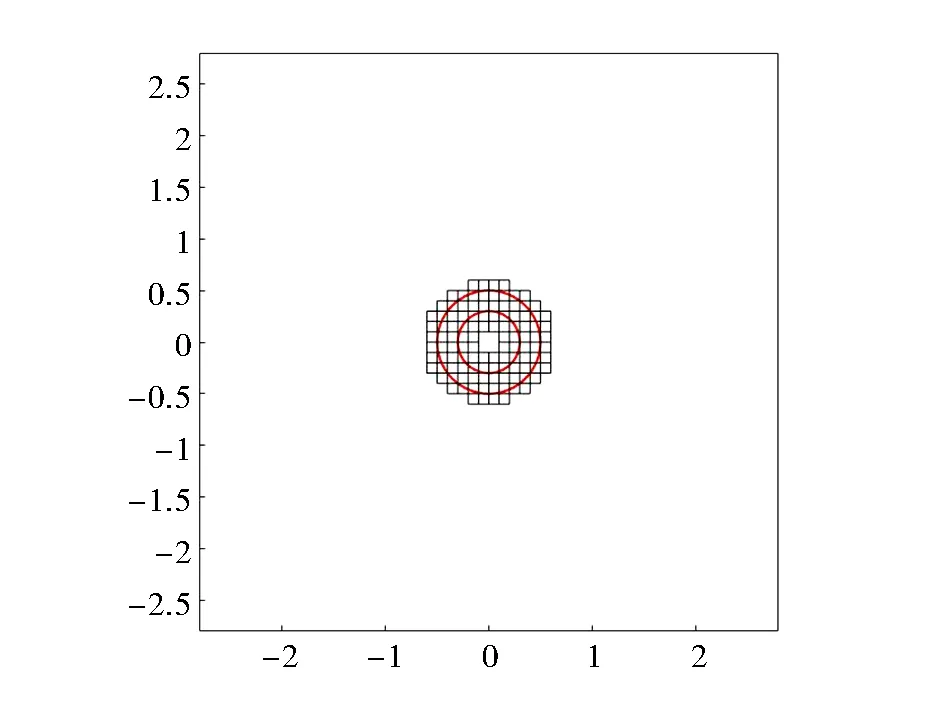
图11 第三次迭代反演的结果

图12 第四次迭代反演的结果

表3 各次迭代网格点信息

4 结 论

本文提出了由散射场的近场数据来反演定态Schrödinger方程中位势支集的多水平采样算法。多水平采样算法是一种迭代过程，它在每次迭代中将抽样域D进行细分，并根据阈值来保留、删掉一些网格点来近似找到位势支集的形状和位置。多水平采样算法只进行矩阵和向量运算，不涉及任何优化和求解不适定性方程的过程。该算法一般只需要较少的入射场数，阈值也很容易设定。此外，多水平采样算法收敛速度快，可以很容易地分离出支集中多个不相交的部分，通常只需要几次迭代就能近似找到每个部分的满意初始位置。多水平采样算法还有一个优点，就是它能自动修正之前的迭代结果，具有很强的自适应性。