SH分子辐射跃迁的理论研究

刘鑫鹏, 李星月, 徐林轩, 李 瑞, 李奇楠, 罗 旺

(齐齐哈尔大学 理学院, 齐齐哈尔 161006)

0 引 言

人体中存在大量含有SH分子的功能蛋白, 其在稳定蛋白质构象和保持蛋白质活性方面起到重要作用[1]。在天体物理方面由于宇宙中硫含量相对较高, 已经有人对SH分子进行了观测[2-3]。SH分子在生命科学和天体物理等领域均有重要作用。因此, SH分子的分子结构和分子光谱的研究对其反应机理和反应产物的理解具有重要的参考意义, 已经引起了人们的广泛关注。

在实验上, 许多学者都观测到了SH分子的光谱[4-9]。 在早期工作中, Porter和Ramsay使用闪光光解装置对SH的吸收光谱进行了拍摄, 获得了SH分子的一些光谱常数[4-5]。 随后, Johns记录了SH分子的A2Σ+-X2Π跃迁的(2, 0)谱带, 并获得了更准确的X2Π态的解离能 (3.53±0.12)eV[6]。 Morrow等又利用闪光光解装置获得了SH分子的真空紫外吸收光谱, 观察到了从基态X2Π到7个激发态的跃迁[7]。 Schnieder等应用原子光谱技术得到了A2Σ+态的势阱深度 (9 280±600) cm-1, 从而可以获得更为精确的X2Π的解离能 (3.71±0.07) eV[8]。在SH的激光诱导荧光实验中, Ubachs等根据线宽测量显示, 存在预解离[9]。在1997年, Wheeler等通过光腔衰荡光谱技术研究了SH分子的A2Σ+态的预解离, A2Σ+态的各个振动-转动能级的线宽测量结果表明，预离解速率随着振动量子数的增加而增加[10-11]。

在理论研究方面, Hirst等使用从头算的MRD-CI方法计算了SH分子,并指出只有X2Π和A2Σ+是束缚态[12]。Hirst等基于理论计算的垂直激发将B2Σ态指认为2Σ-态, 随后，Park的计算结果也证明了这一点[13]。Senekowitsch等计算了SH分子辐射的跃迁几率, 给出了电偶极矩[14]。Bruna用从头算的MRD-CI方法对SH分子进行了计算, 得出了束缚态X2Πi和A2Σ+的光谱常数和电偶极矩[15]。随后, Resende等在CASSCF-MRCI/aug-cc-pV5Z理论水平下, 计算了SH分子与三个解离极限H(2S)+S(3P,1D,1S)相关的二重态和四重态, 还确定了X2Π-A2Σ+系统的跃迁偶极矩[16]。2008年, Brites等使用从头算的Aug-cc-pV6Z/MRCI方法对SH(A2Σ+、 a4Σ-、 B2Σ-和 b4Π)的势能曲线进行了精确的计算, 结合费米-黄金规则,推算出SH的A2Σ+态的振动能级的预离解速率[17]。

综上所述, 早期对于SH的理论研究方面, 主要集中在电子结构的计算。在最近的理论研究中, 用有效势代替芯价电子, 但是只计算了少数价电子。Bruna[15]和Brites[17]的理论计算虽然包含了电子关联效应和自旋-轨道耦合效应等精细效应对结构的影响, 但是他们仅关注能量较低的几个电子态的势能曲线。因此, 本文采用考虑Davidson修正的多参考组态相互作用(MRCI+Q)方法对SH的电子结构进行了系统研究。为了提高计算精度, 计算中考虑了标量相对论效应, 芯-价电子关联效应(CV)对电子结构的影响。给出了与最低三个解离极限相关的8个Λ-S态的势能曲线。拟合了光谱常数, 计算了8个Λ-S态的电偶极矩随核间距的变化, 并分析了电子态的组态成分变化对电偶极矩的影响。计算了B2Σ-、 a4Σ-、 b4Π 和A2Σ+态之间的自旋-轨道耦合矩阵元, 阐明了A2Σ+态的预解离机制。基于电子结构的计算, 本文还研究了SH分子的辐射跃迁性质, 给出了电子态之间的跃迁偶极矩(TDMs)和Franck-Condon因子(FCFs) ,分析了电子态振动能级跃迁的强弱。

1 计算方法

使用MOLPRO程序[18]计算了SH分子的三个最低解离极限相对应的8个Λ-S态的电子结构。根据Winger-Witmer规则, 通过式(1)确定8个Λ-S电子态与三个最低解离极限的原子状态之间的关系：

S(3Pg)+H(2Sg)→(2Σ++2Π)+(4Σ-+4Π)

S(1Dg)+H(2Sg)→(2Σ++2Π+2Δ)

(1)

S(1Sg)+H(2Sg)→(2Σ+)

通过分离原子法获得了SH分子的三个最低解离极限对应的8个Λ-S态。 在开展SH分子的电子结构计算之前, 还测试了S和H原子的基组。最后, 选择考虑芯壳层-价壳层电子关联效应的全电子Aug-cc-pwCV5Z-dk基组[19-20]。SH分子的对称点群为C∞v。然而，MOLPRO程序只能在阿贝尔群下开展计算。因此，选用C∞v群的阿贝尔子群C2v来计算SH分子的电子态。C∞v群的不可约表示与阿贝尔子群C2v的不可约表示具有以下的对应关系：Σ+=A1、Π=B1+B2、Δ=A1+A2和Σ-=A2。在R=0.09～1.0 nm内的一系列离散的核间距上, 本文采用以下三个步骤计算8个Λ-S电子态的本征能量。首先, 采用Hartree-Fock(HF)方法计算SH分子X2Π态的单组态波函数。以HF方法得到的单组态波函数作为初始波函数, 采用完全活性空间自洽场方法(Complete active space self-consistent field， CASSCF )[21]优化初始波函数获得参考波函数。 最后, 在CASSCF计算的参考波函数的基础上, 应用多参考组态相互作用方法(MRCI)[22]计算了8个Λ-S电子态的本征能量。在CASSCF计算中活性空间的选取是非常关键的, 本文测试了不同活性空间对计算精度的影响。最后, 选择与S原子的3s3p价壳层和H原子的1s价壳层对应的分子轨道作为CASSCF计算的活性空间, 即C2v对称性下的3个a1,1个b1和1个b2对称性的分子轨道。由于MRCI计算的能量不具有大小一致性。因此,本文引入Davidson修正(+Q)来考虑更高电子激发来消除大小一致性的误差[23]。在MRCI计算中, 1s2s2p壳层的10个电子被放入闭壳层。闭壳层中的10个电子通过单激发和双激发相互关联。也就是说, 在MRCI计算中, 考虑SH分子的17个电子的关联效应, 在本工作中将其表示为MRCI+CV。为了阐明芯-价关联效应对电子结构的影响, 将1s2s2p壳层中的10个电子放入冻结的芯轨道不作关联, 其结果用MRCI表示。通过对比MRCI+CV和MRCI结果, 可以得到CV效应对电子结构的影响。为了考虑相对论效应对电子结构的修正, 通过计算三阶Douglas-Kroll和Hess电子积分获得标量相对论效应[24]。

基于MRCI+Q计算获得的Λ-S电子态的势能曲线, 应用Level程序[25]获得束缚态的光谱常数。给出了电偶极矩随核间距变化的曲线。此外，还确定了不同电子态之间跃迁偶极矩和Franck-Condon因子, 分析了预解离机制。

2 结果与讨论

2.1 SH分子的Λ-S态的势能曲线和光谱常数

图1 SH分子的Λ-S态的势能曲线Fig.1 Potential energy curves of Λ-S states of SH molecule

采用高精度的MRCI+Q方法对SH分子的8个Λ-S态进行了研究。 理论计算获得的SH分子的8个Λ-S态的势能曲线(PECs)如图1所示。8个Λ-S态以基态X2Π的平衡位置处的能量作为零点, 其中X2Π和A2Σ+是束缚态, 其他6个态B2Σ-、 C2Δ、 D2Π、 E2Σ+、 a4Σ-和b4Π是排斥态。通过计算, 得到S原子的1Dg-3Pg、1Sg-3Pg能量间隔分别为8 687和21 634 cm-1, 与已观测到的实验值9 043和21 984 cm-1[26]相接近。此外, 由于第一激发态A2Σ+的势阱非常接近高密度电子态区域, 所以A2Σ+的势能曲线与三个排斥态a4Σ-、 B2Σ-和b4Π相互交叉。

根据图1中的势能曲线, 通过数值方法求解SH分子的一维核运动Schrödinger方程，获得了光谱常数, 包括平衡核间距Re、 绝热激发能Te、 简谐振动常数ωe和非谐性常数ωeχe, 以及平衡转动常数Be和解离能De, 相关参数如表1所示，其中还列出了前人研究的实验和理论结果以便于比较和参考。此外, 为了阐明CV效应对SH分子的电子结构影响, 通过包含和不包含CV效应两种不同方法得到的光谱常数如表1所示。8个Λ-S态在R=0.135 nm处的主要电子组态及其所占百分比如表2所示。基态X2Π主要由开壳电子组态4σ25σ22π3(98.0%)组成, 比较包括和不包括CV效应的X2Π的光谱常数, 可以发现CV效应引起的ωe、ωeχe、Re和De修正为50 cm-1、 5.090 4 cm-1、 -0.000 09 nm和-0.038 6 eV。当考虑CV效应时, 计算出的ωeχe、Re和De更接近实验值60 cm-1、 0.134 nm和3.7 eV。第一激发态A2Σ+的主要电子组态为4σ25σ12π4(96.6%), 对应于X2Π态电子组态的单电子激发(5σ→2π)。在没有包含CV效应的情况下, 计算得到的Te、ωe、ωeχe和Re分别为30 639 cm-1、 2 111 cm-1、 119.982 7 cm-1和0.142 14 nm, 与实验值相差-399 cm-1、 128 cm-1、 34.170 1 cm-1和-0.000 16 nm。当包括CV效应时,Te、ωe、ωeχe和Re的值分别校正了990 cm-1(3.1%)、 113 cm-1(5.7%)、 11.837 4 cm-1(9.9%)、 0.000 22 nm(0.02%), 并且本文计算的Te、ωe、ωeχe的结果与实验值之间的偏差仅为591、 18和22.332 7 cm-1。 通过对比包含和不包含CV效应的结果, 可以看出，CV效应很好地描述了芯电子和价电子的关联效应, 考虑CV效应后的结果更加接近实验值。

表1 SH分子Λ-S态的光谱常数

表2 SH分子电子组态成分及其所占百分比

2.2 SH分子的Λ-S态的电偶极距

SH分子的8个Λ-S态的电偶极矩(DMs)随着核间距变化的曲线如图2所示, 基态X2Π的电偶极矩为0.27 967 a.u., 与Byfleet等观测的实验结果0.2 439 a.u.相吻合[28]。A2Σ+的电偶极矩曲线在R=0.16 nm处存在峰值, 峰值为0.56 305 a.u.。电偶极矩的变化能很好地反映出电子组态成分的变化。a2Σ-、 C2Δ、 B2Σ-和E2Σ+的电偶极矩变化趋势大致相同, 这是因为它们的主要电子组态均为4σ25σ26σ12π2。此外, 由于b4Π和D2Π的主要电子组态都是4σ25σ16σ12π3, 它们的电偶极矩也有相似的变化趋势。还可以看出，当核间距R趋近于无穷大时, 电偶极矩的数值均趋近于零。分子的电偶极矩反映分子的正电荷分布与负电荷分布的分离状况，即分子电荷系统的整体极性。根据分离原子方法，若处于较大核间距R的两个中性原子均不带电，这时准分子体系的电偶极矩为零。因此，在较大核间距R时, 趋近于零的分子电偶极矩表明解离产物为中性原子。

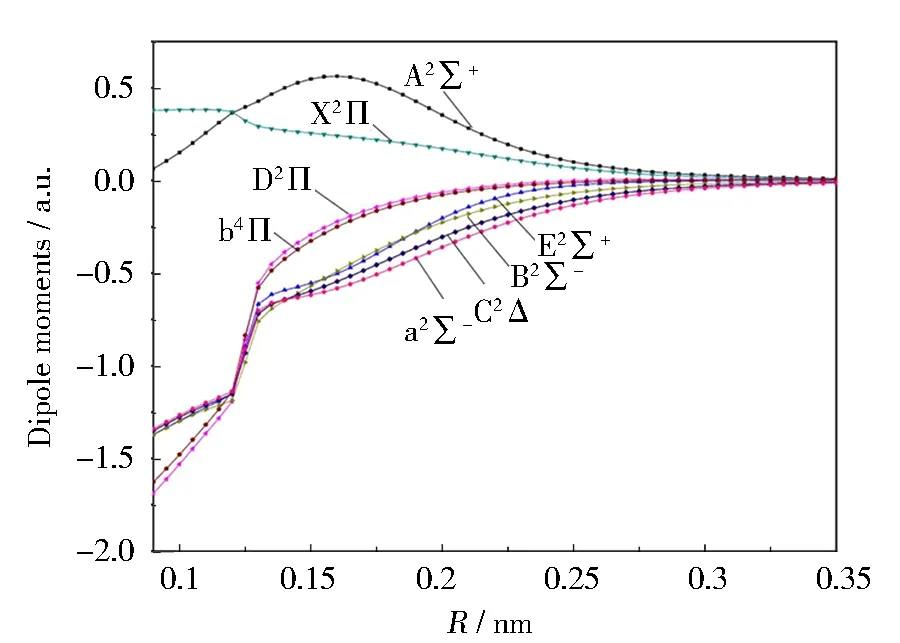
图2 SH分子Λ-S态的电偶极矩随核间距的变化

图3 A2Σ+-X2Π、B2Σ--X2Π、 C2Δ- X2Π跃迁偶极矩随核间距的变化

2.3 SH分子的跃迁性质和预解离

在MRCI计算的基础上, 研究了SH分子的跃迁性质。首先, 计算了SH分子从激发态到基态的跃迁偶极矩(TDMs)。使用Level程序计算了X2Π态到A2Σ+态的Franck-Condon因子(FCFs)。SH分子A2Σ+-X2Π、B2Σ--X2Π和C2Δ-X2Π之间的跃迁偶极矩沿核间距R的变化规律如图3所示。可以看到, A2Σ+-X2Π、B2Σ--X2Π和C2Δ-X2Π三条跃迁偶极矩曲线在核间距R趋近于无穷大时, 跃迁偶极矩均趋向于零。其中B2Σ--X2Π和C2Δ-X2Π跃迁偶极矩曲线趋近于零的速度非常快, 而A2Σ+-X2Π的跃迁偶极矩曲线相对于B2Σ--X2Π和C2Δ-X2Π较为平缓。图中显示C2Δ-X2Π跃迁的TDM明显小于B2Σ--X2Π跃迁的TDM, 这是由于波函数空间在C2Δ态X2Π状态之间的重叠很小而引起的。

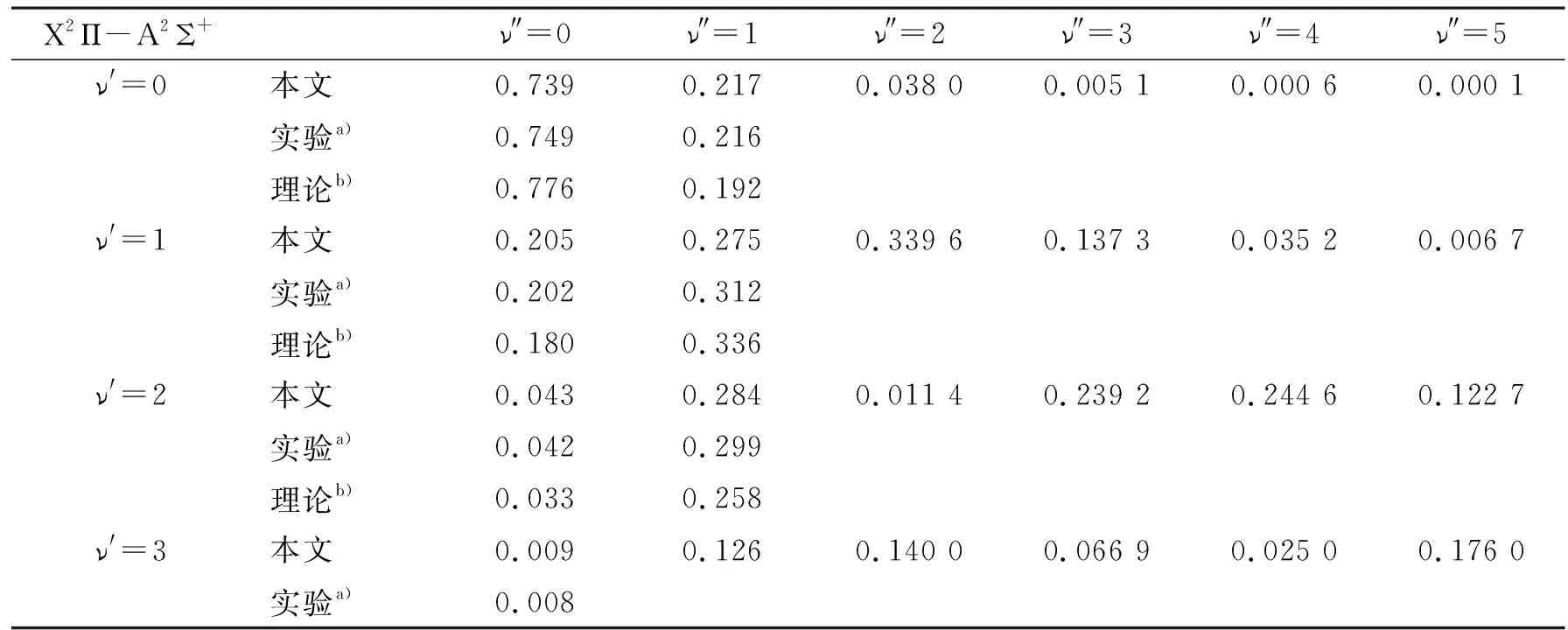
表3 SH分子激发态跃迁的Franck-Condon因子

利用Level程序计算了X2Π-A2Σ+跃迁的Franck-Condon因子, 结果如表3所示。这些FCFs随振动量子数ν′或ν″呈现出不规则的变化规律。计算结果与Johns的实验结果[6]非常符合, 而且相比于Bruna的理论结果[15]更加接近实验值。

为了定量地研究电子态之间的扰动作用对A2Σ+态的振动能级的预解离的影响, 本文应用费米-黄金规则计算了A2Σ+态的振动能级的预解离速率随振动量子数的变化。应用从头计算得到的A2Σ+和B2Σ-、 a4Σ-、 b4Π的自旋-轨道耦合矩阵元[29], 获得了B2Σ-、 a4Σ-、 b4Π态分别对A2Σ+态的较低振动能级的预解离速率的贡献。费米-黄金规则的计算式为[30-31]:

(2)

式中：ks(v,J)为预解离速率, s-1；ψE,J’(r)和ψv,J(r)分别为初始束缚态的径向波函数和末态的连续波函数。Ms(r)为初始态和末态的耦合函数:

Ms(r)=〈ψv,J(r)|HSO|ψE,J′(r)〉

(3)

预解离线宽(ГFWHM)和预解离速率(ks(v,J))之间的表达式为:

ΓFWHM=ΣSks(ν,J)/2πc

(4)

式中c为光速, 预解离线宽要考虑所有可能引起预解离的末态的贡献。

应用Bcont程序[30-31]计算了B2Σ-、 a4Σ-、 b4Π态对A2Σ+态较低振动能级的预解离速率, 并应用式(3)计算了这些电子态导致的A2Σ+态的振动态的预解离线宽。理论计算的B2Σ-、 a4Σ-、 b4Π态引起的A2Σ+态ν′=0-7振动能级的预解离线宽的变化曲线如图5所示。A2Σ+的ν′=1和ν′=2振动能级的预解离线宽主要起源于a4Σ-态的扰动作用。当振动量子数ν′增加到大于3时, A2Σ+振动能级的预解离线宽主要来自b4Π-A2Σ+预解离通道的贡献。B2Σ-态对A2Σ+态振动能级的预解离线宽的贡献较小。

3 结 论

应用MRCI+Q方法计算了SH分子的能量最低的三个解离极限(S(3Pg)+H(2Sg)、 S(1Dg)+H(2Sg)和S(1Sg)+H(2Sg))对应的8个Λ-S态的电子结构。计算中考虑了标量相对论效应和CV效应对电子结构的修正。基于考虑各种物理效应的电子态的势能曲线, 应用数值方法求解分子的核运动Schördinger方程得到了束缚态的光谱常数, 本文理论计算的光谱常数与实验结果吻合较好。应用MRCI方法计算了8个Λ-S态的电偶极矩曲线, 分析了电子组态成分的变化对电偶极矩的影响。基于理论计算的B2Σ-、 a4Σ-、 b4Π态和A2Σ+态的自旋-轨道耦合矩阵元, 并应用费米-黄金规则计算了A2Σ+态的振动能级的预解离速率和预解离线宽随振动量子数的变化。通过A2Σ+态的振动能级的预解离线宽随振动量子数的变化规律, 阐明了B2Σ-、 a4Σ-、 b4Π态对A2Σ+态的扰动所引起的预解离机制。本文给出了考虑各种物理效应的SH分子的基态和激发态的电子结构,借助于电子之间的自旋-轨道耦合矩阵元和费米-黄金规则得到了A2Σ+态的振动能级预解离参数,为SH分子激发态的指认提供了精确的辐射跃迁性质。