无界粗糙面与障碍复合电磁散射数值研究
汤翼阳, 张 磊,2
(1.黑龙江大学 数学科学学院, 哈尔滨 150080; 2.黑龙江大学 黑龙江省复杂系统理论与计算实验室, 哈尔滨 150080)
0 引 言
关于麦克斯韦方程刻画的粗糙面电磁散射问题研究目前有很多结果。Li等使用完美匹配层(PML)方法研究了截断的无界粗糙面电磁散射问题,证明了截断PML问题存在唯一解,并给出了散射问题解与截断PML问题解之间的显式误差估计[1]。Zhang等研究了点源入射情形下,由无界粗糙表面隔开的两层有耗介质中完美导体障碍物的电磁散射问题。给定入射点源以及障碍物和无界粗糙面,所谓的正问题是确定此时电磁波场的分布,相关的反问题是根据未知物体上方和粗糙表面下方的散射场和透射场观测数据,重建障碍物和无界粗糙面。他们在论文中证明了正问题的适定性和反问题的唯一性[2]。Desanto采用了基于格林函数摄动的方法,得到了相应的卷积方程,并利用散射理论解释了水平发射水平接收极化与垂直发射垂直接收极化比超过1的海尖峰现象[3]。Saillard等发现粗糙表面雷达散射截面在掠入射时变得非常小,随后基于一种特殊的积分形式建立了一个适用于低掠入射角和散射角的方法[4]。Zhou把三维空间中散射问题转化为研究二维表面场分布的问题并加以解决[5]。Asirim利用有限元方法分析了粗糙表面的电磁波散射问题和不同表面上的散射场分布[6]。Benali等研究了任意形状导体及介质粗糙表面的电磁散射问题,数值计算了任意形状障碍体电磁散射的能量密度分布,得到了一类波场随表面变化时的散射场分布规律[7]。Liu等提出了一种MPSTD算法,用于分析埋在粗糙表面下方的三维障碍物的电磁散射[8]。Haddar等在适当的Sobolev空间中,给出了无界区域中透射层状结构电磁散射问题的变分公式[9]。Nguyen提出了一种求解三维各向异性Maxwell方程周期散射问题的体积积分方程方法[10]。Bao等研究了无穷结构中时谐声波障碍散射问题,证明了问题的适定性和相应反问题的唯一性[11]。Zhang等研究了障碍复合散射问题的数值解法,并给出了利用有限孔径数据同时重建障碍物和无界粗糙面的直接成像方法[12]。
本文研究了电磁波入射无界粗糙表面与障碍体复合散射问题,结合完美匹配层技术,使用有限差分方法对带有适当边界条件的时域Maxwell方程进行数值求解,并进一步分析粗糙表面和障碍体的形状、参数对散射场的影响。
1 粗糙表面复合散射问题
1.1 散射问题数学模型
假设S是一个无界粗糙面:
S={x=(x,y)∈3:z=f(x,y)}
式中f∈C2(2)。因此,曲面S将整个空间3划分为上半空间Ω1和下半空间Ω2。其中
Ω1={x∈3:z>f(x,y)}, Ω2={x∈3:z 假设Ωk域被均匀、各向同性介质填充,其特征是介电常数εk>0, 磁导率μk>0,电导率σk>0,k=1,2。 用Γj={x∈3:z=hj},j=1,2分别表示粗糙面上方和粗糙面下方的平面,其中h1和h2满足: -∞ 当交界面可穿透时,透射边界条件为: 当表面不可穿透时,交界面边界条件为: 电磁场在无穷远处满足向外传播辐射条件[1]。 粗糙面下方电场与磁场情形可同理得到。 对其进行整理,可得: ⟹ 同理,可得其余两式的离散格式: 整理得: 同理可得: 使用同样的方法,对粗糙面上方TM波在时间和空间上进行差分离散,可得: Ca(m)、Cb(m)、Cp(m)、Cq(m)分别为: 图1 UPML吸收边界Fig.1 Absorbing boundary of UPML 为了计算无界区域的电磁散射问题,在区域的截断边界处需要给出合理的边界条件,本文使用单轴完美匹配层(UPML),如图1所示。在单轴各向异性介质中,电磁波仍满足Maxwell方程,所以只要设置合适的单轴参数,UPML吸收介质中的差分方程对整个FDTD计算区域都是适用的。二维情形中UPML的截断边界包含了4个棱边区和4个平面区。棱边区是两条边,这个交界面表示的是从一种单轴介质到另一种单轴介质。 式中σ1为几何图中粗糙面上方与UPML层相邻的内部介质的电导率。sx=κx-σ1x/iωε0,sy=κy-σ1y/iωε0。将新的参数代入到TM波公式,可得: 为了保证算法的稳定性,采用Courant稳定性条件,即,对于二维情况空间和时间离散步长满足: 通过数值实验验证PML边界的有效性,同时模拟不同位置入射点源以及表面上方不同障碍体对散射波场分布的影响。取入射波频率为5 GHz,交界面函数y=20Δy+sin(x-300Δx)Δx,其长度L=600Δx(Δx=Δy=λ/20),表面上方圆形障碍物圆心位于(300Δx,60Δy),半径为r=10Δx,PML层厚度为8Δx,针对假设表面不可穿透情况,给出不同时刻的波场分布图,如图2所示。 图2 时间步长T=200、400、600、800时电磁场分布 图中Ex、Ey、Ez分别表示电场在空间中的分量,Hx、Hy、Hz分别表示磁场在空间中的分量。可以看到,波场在PML中没有产生明显的反射,故实验有效地实现了对波场的吸收,并模拟了电磁波粗糙面与障碍复合电磁散射。


2 时域有限差分格式
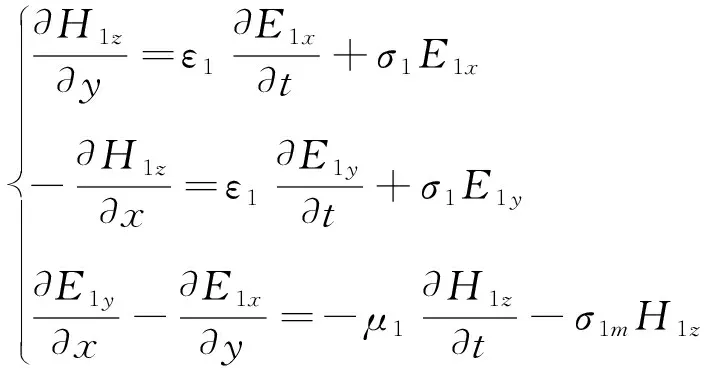

2.1 有限差分格式
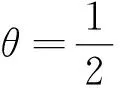


2.2 吸收边界


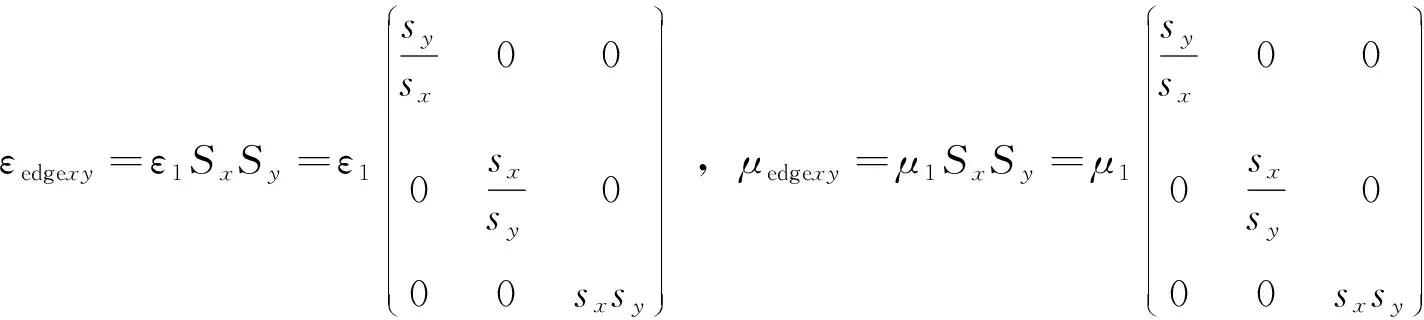
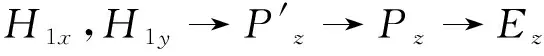

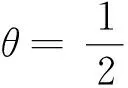
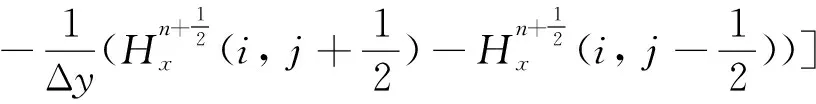


3 数值实验





