基于启发式教学的小学生常用解题方法研究

河南省平顶山市新华区教师培训中心 吕建英

一、问题的提出

教育要落实立德树人根本任务，提升自主创新能力，培养担当民族复兴大任的时代新人。爱因斯坦说过，提出一个问题往往比解决一个问题更重要，因为发现问题是创新的前提，开拓学生思维。在课堂教学中，若能主动提出问题，并培养学生提问题、培养学生创新意识，这样不仅使学生的创新思维得到发展，还能激发学生学习创造的主动性、积极性。启发式教学在课堂上的广泛运用使学生由原来的听记教师讲授内容转变到学生围绕教师提出的问题进行思考回答，这种教法能调动学生思维的积极性，培养学生思考问题、解决问题的能力。我们经常见到有的教师为了提高学生学习成绩，采用题海战术，最终结果是教师苦、学生累，学习成绩也没有得到应有的提高，原因何在？我们应教给学生哪些解题方法呢？本文做了一些探讨。

二、小学生常用解题方法研究

（一）指导学生学会借助直观解决问题的方法

数学知识具有高度的抽象概括性，而小学生的思维又以具体形象思维为主，如何解决这个矛盾呢？教学中常用动手操作、直观演示的教学方法来化解这一矛盾。教师在教学中大量采用这种教法让学生多种感官参与教学，引导他们在活动中思考、在思考中活动，因而这种教法也无形中影响着学生的学习，当儿童遇到一些问题时，也会像教师一样设法借助直观帮助思维，寻找解决问题的办法，这即是一种学习的方法。

义务教材中，大量的例题的讲解是通过直观演示、动手操作来解决的，这无疑对学生掌握这一方法起了示范作用。例如，教学10 以内数的组成和20 以内的进位加法都是通过摆小棒的方法来解决的。又如，长方形面积的计算是通过摆单位面积的正方形而逐步推导出来的。只要我们长期这样训练，就能使学生在不自觉中掌握这一方法。

（二）指导学生学会利用化归法解决新问题、学习新知识

在解决某一新问题时，先对它进行变形，使其归结为另一个熟知的、简单的问题，再通过这个熟知或简单问题的解决，把解得的结果作用于原问题，从而使问题获得解决。这种解决问题的方法叫作化归法。

化归法是解决数学问题最常用的方法，因为数学知识联系性比较强，往往是旧知识是新知识的基础，新知识是旧知识的延伸和发展，特别是在小学中、高年级，许多知识是在旧知识的基础上通过分析、综合、抽象、概括得到的，从小让儿童学会用自己掌握的熟悉的旧知识去解决新问题、探求新知识非常有益，学生的认识也就是在这种化归过程中，不断促进新的认知结构的建立。学生一旦掌握了这种解决新问题、学习新知识的方法，就像得到了一把通向未来大门的创新金钥匙。

化归的方法孕伏在各类知识中，体现在知识的揭示、应用过程中。因此，教师应深入钻研教材、挖掘各种转化因素，在课堂教学中，着力展现化归的过程。例如，学习除数是小数的除法时，应着力展现利用商不变的性质把除数是小数的除法转化成除数是整数的除法而最终加以解决的过程。又如，教学异分母分数加减法应着力展现通过通分把它化归成同分母分数加减法而最终得以解决的过程。

在教学中，当学生遇到新问题时，我们要问一问学生：“能不能把它化成你们已经学过的知识呢？”在教学中长期坚持让学生用化归法去探求新知识、解决新问题，那么学生解决问题的能力一定会提升。

（三）指导学生学会用画图法帮助解答问题的本领

题目的数量关系，一般都具有抽象性与隐蔽性的特点，所以很多学生都有解答问题的题目困难的感觉。克服困难，学会解答的方法很多，其中用画图法帮助解决是很重要的一种。因为数学是研究现实世界的空间形式和数量关系的科学。数与图的有机结合，有利于分析题目中的数量关系，丰富表象、引发联想、启发思维、拓宽思路、化难为易。因此教师要把学会用画图法帮助解答这一法宝教给学生。

要培养同学们画图的技能，一方面教师在教学时要采用先画图分析，然后列式解答的方法，给同学们做出画图的示范；另一方面要加强练习，简单的题目就要求同学们画图分析，一些较复杂的解决问题题目及典型的解决问题题目（特别是行程问题）也让同学们画图分析，分数、百分数应用题还让同学们画图分析。长期坚持训练，同学们就逐步掌握了用画图法帮助解答问题的本领。

（四）指导学生学会用分析综合法解答问题的方法

每一道解决问题的题目都包括已知条件和所求问题两个部分。解答的过程就是如何根据已知条件，设法求出所求问题的过程。分析的常用方法有两种：一是从已知条件出发，根据数量关系先选择两个已知数量，提出可以解决的问题，然后把所求出的数量作为新的已知条件，与其他已知条件搭配，再提出可以解决的问题。如此继续下去，一直到推出要求的结果为止。这种思考问题的方法称为“综合法”。另一种是由问题入手，按照与上述方法相反的顺序，逐步推出已知条件，这种思考问题的方法称为“分析法”。换句话说，综合法是“由因索果”，分析法就是“执果索因”。

（五）指导学生掌握用逆推法解答问题的方法

逆推法思考问题的特点不是从问题的条件到结论，而是倒过来从问题的结论本身出发，或者从结论的反面入手，一步一步地找到结论成立的条件，从而达到使问题获得解决的目的。

逆推法是解答数学题常用的一种方法。如果一道题目给出了未知数经过某些运算而得到的最后结果，这时从正向分析比较困难，教师就要引导学生使用逆推法。

例如：某数减去11 后，扩大1000倍，再缩小20 倍，正好是1000。求某数是多少？

引导学生从最后一个条件“正好是1000 ”入手向前推算

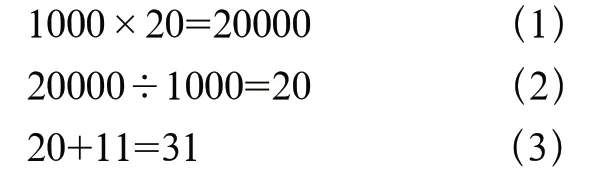
使用逆推法需要注意的是一切都要与顺向的反着来，遇加用减，遇减用加，变乘为除，变除为乘，最后求出答案（结果）。

（六）指导学生学会用假设法解决问题的方法

根据题目中的已知条件或结论，假定某种现象成立，然后进行推算，当所得的结果与题意发生矛盾时，再找出产生矛盾的原因，进行适当的调整，消除差异，使问题得到解决。这种思考问题的方法叫作假设法。

假设法是一种重要的思考问题的方法。同学们在做题时，往往遇到直接推理或逆转推理都找不到解题途径的情况，这时采用假设法可以使题目中隐蔽或复杂的数量关系明朗化和简单化。

例如：一次智力测验有10 道题，每答对一题得3 分，每答错一题扣除2 分。小红答完了解10 道题，只得了20 分。她答错了几题？

这一题采用直接推理很难找到解题思路，这时可采取假设法。假设小红10 道题都答对了，那么她应得3×10=30（分）。为什么小红只得了20 分呢？因为她答错了一部分题。每答对一题得3 分，每答错一题扣2 分，也就是说每答对一题与每答错一题相差3+2=5（分）。小红得了20 分，比全部答对少了30-20=10（分），所以小红答错了10÷5=2（道）。

（七）指导学生掌握用守恒法解答问题的方法

在复杂的数量关系中，有一不变量。通过分析这一不变量作为解题的突破口，从而使问题最终得以解决的解题方法叫作守恒法。

当学生遇到数量关系较为复杂，用分析综合法、逆推法、假设法等方法都不能解决的问题时，可让学生找一找题中有没有不变的量，通过对这一不变量的分析，打开解题思路，从而使问题最终得以解决。