追根究底觅本质 抽丝剥茧启思维

刘丽霞 林应宏

◆摘  要：现代教学论认为数学教学，实质上是数学思维活动的教学，没有思维，就谈不上数学教学，更谈不上培养能力、开发智力，因为思维是智力的核心。该文以“圆柱的侧面积”的教学为例，策划有效的学习活动，在创设情境、操作实验、推理归纳的过程中，训练学生的数学思维。让学生在数学活动中体验、感悟和反思，从而获取经验，提高学生的数学素养。

◆关键词：数学思维;猜想;验证;经验

荷兰哲学家斯宾诺莎说过：“智慧，不是死的默念，而是生的沉思。”数学思维是以数和形为对象，以数学语言和符号为载体的一种思维活动，数学思维具有抽象性、整体性、相似性、问题性等特征。训练学生的数学思维是数学教学的核心任务。数学思维训练如同抽丝剥茧，不能一刀剪开，而要由外到内，一根一根地抽取，才能得到完整的“丝线”。下面以“圆柱的侧面积”这一课的教学为例，论述如何引领学生追根究底寻觅本质，抽丝剥茧展现思维。

一、创设情境中联想猜测——启萌直觉思维

在小学数学课堂教学中，教师应为学生创设感性情境，诱导学生在观察中联想，从而产生瞬间顿悟，发现事物的内在联系。

例如，在“圆柱的侧面积”一课的教学中，老师给学生播放了一段压路机工作的视频，着重引导学生观察压路机的工作方式，观察滚筒滚动后留下的印迹，让学生思考讨论：压路机滚动后留下的痕迹是什么形状的？直观形象的情景让学生懂得滚筒滚动一周后，所留下的印迹是长方形，建立了初步的表象。

【教学片段一】验证猜想，获取初步活动经验

师：伟大的发现多源于猜想，今天，我们就来猜想一下，圆柱的侧面展开能得到什么形状 ？

生1：长方形。

生2：正方形。

师：请同学们拿出课前自制的笔筒，把贴在笔筒侧面的彩纸剪开，验证你的前猜想是否正确。验证之前，先想想可以怎样剪。

生1，：直接用剪刀剪开。

生2：可以先在圆柱的侧面上画一条直线，再沿着这条直线剪开，这样可以使边缘齐整。

生3，：在圆柱的侧面上画出高，然后沿着高剪开，就可以知道是什么图形了。

师：把剪开的彩紙恢复成圆柱的侧面，用心观察，你有什么发现？ 请大家分小组讨论，然后进行交流和分享。

组1：展开得到的长方形的大小和圆柱侧面的大小相等。

组2：展开得到的长方形的面积等于圆柱的侧面积。

组3：展开得到的长方形的长是圆柱的底面周长。

组4：长方形的宽是圆柱的高。

活动到此，本课时的教学任务似乎已经完成，学生已具备了初步的活动经验，那么是不是只要再通过练习来巩固学生的经验就可以了？ 答案是否定的。教学要为学生的可持续发展服务，学生可持续发展的动力来源于思维的发散与创新。也就是说，当学生缺乏基本活动经验时，应让学生根据指令进行操作以获取活动经验;当学生具备一定的基本活动经验时，就要放手让学生自主操作，从而丰富活动经验。

二、动手操作中模拟实验——启发形象思维

数学探究如同科学研究一样，同样要经历“猜想——实验——结论”的过程，学生在直觉思维下的猜测为接下去的探究定准了方向，接下去要做的是顺藤摸瓜，一步步探寻问题的本质。实验验证是至关重要的一步，学生可通过亲手操作验证自己的猜测。

【教学片段二】运用经验，深入探究

师：对于圆柱侧面的展开你还想探究什么问题？

（学生动手操作，将圆柱的侧面剪开后展开，研究圆柱的侧面积计算）

师：大家还发现了什么？

生1：我们把圆柱的侧面展开后得到一个长方形，这个长方形的长就是圆柱的底面周长，宽是圆柱的高。

生2：圆柱的侧面积就是这个长方形的面积。

生3：要求圆柱的侧面积，只要量出这长方形的长和宽就行了。

生4：也就是说圆柱的侧面积应该等于底面周长乘高。

师：同学们真会动脑筋，得出了圆柱侧面积的计算方法……

（这时，有一生欲言又止，手举了又放下，眼中充满疑惑，教师示意他大胆发言）

生：大家看，（边说边出示他的圆柱侧面展开图）我刚才把圆柱侧面剪开时，剪歪了，结果展开后得到的不是长方形，那面积还等于圆柱的底面周长乘高吗？

师：（把问题抛给了大家）咦，这样还能证实圆柱的侧面积等于圆柱的底面周长乘高吗？

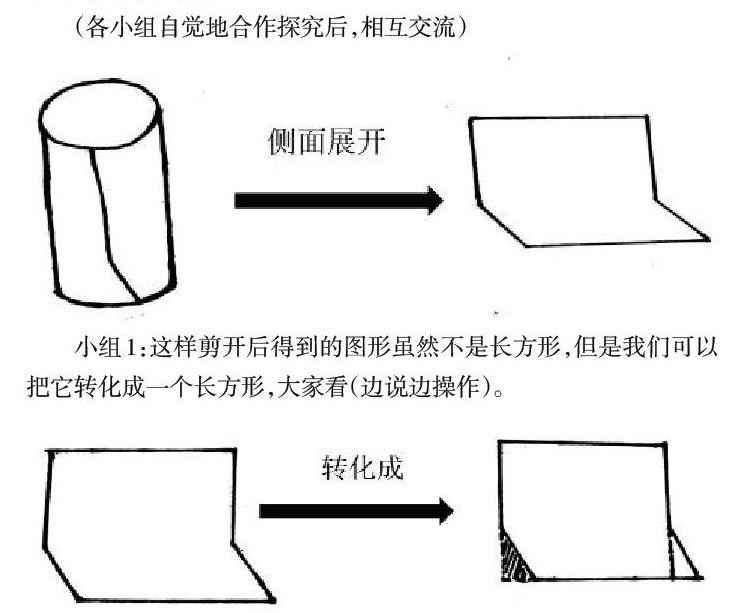
（各小组自觉地合作探究后，相互交流）

小组1：这样剪开后得到的图形虽然不是长方形，但是我们可以把它转化成一个长方形，大家看（边说边操作）。

转化后的长方形的长是圆柱的底面周长，宽是圆柱的高，所以圆柱的侧面积还是等于底面周长乘高。

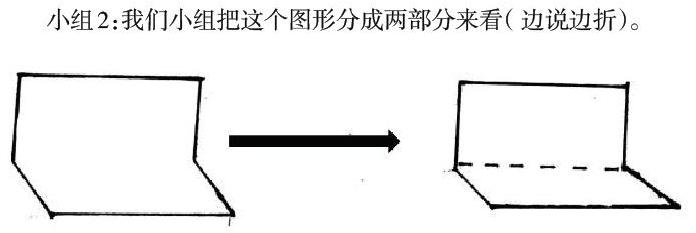
小组2：我们小组把这个图形分成两部分来看（ 边说边折）。

上部分是个长方形，它的长是圆柱的底面周长，宽设为a。下部分是个平行四边形，底是圆柱的底面周长，高设为b。那么，圆柱的侧面积=柱的底面周长×（ a+b）=圆柱的底面周长×高。

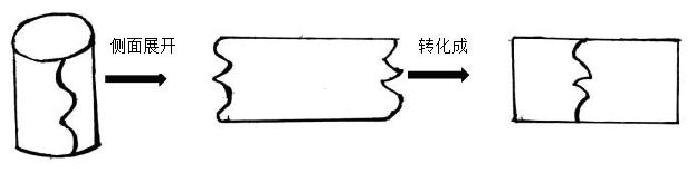
小组3：我们发现，即使随手把圆柱的侧面撕开，得到的图形的面积也是圆柱的底面周长乘高。大家看（ 边说边操作）。

虽然展开后得到的图形不是长方形，但我们可以把这个图形转化成长方形。转化成的长方形的长是圆柱的底面周长，宽是圆柱的高，所以圆柱的侧面积等于底面周长乘高。

整个教学过程，学生探究的热情很高，学得非常积极主动，对圆柱侧面积的计算有了更为深刻的认识。笔者认为，教学成功的关键在于教师关注了学生的学习过程，尊重个体的数学“ 现实”，为学生创设了一个平等、和谐、开放的学习氛围，放手让学生自主探索，充分挖掘“意外生成”资源，从而使学生在获得知识的同时，培养了探究精神，开发了学生的求异思维能力。

三、推理归纳中显露本质——启悟逻辑思维

抽丝剥茧的最后一道程序是“复摇整理”，只有将抽出来的蚕丝整理完毕才算结束。学生的模拟实验只是验证了“可以将圆柱侧面转化为长方形”的猜想，并没有完成整个探究任务，计算圆柱形罐头的侧面积才是问题的核心，推导出圆柱侧面积的计算方法才是问题的本质。

在“圆柱的侧面积”一课的实验探究阶段，教师引导学生理解了“化曲为直”的转化策略后，着重启悟学生逻辑思维，引领学生在推理归纳中显露本质。学生对圆柱侧面展开图与圆柱侧面进行比较分析，和学生共同探寻圆柱侧面与长方形各部分之間的关系：长方形的长与圆柱的底面周长相等，长方形的宽与圆柱的高相等，圆柱的侧面积与长方形的面积相等，因此圆柱的侧面积等于底面周长乘高。显然，逻辑思维在推导圆柱侧面积计算方法的过程中发挥了主导功能，学生通过逻辑推理追根究底，渐渐逼近问题的本质，在层层推理中归纳出圆柱侧面积计算方法。

四、生活实际中延伸拓展——启迪创新思维

2011版《数学课程标准》强调：“数学教学要紧密联系学生的生活实际，从学生的生活经验和已有知识出发，创设生动有趣的情境，引导学生从数学角度去观察事物，思考问题，发展学生的思维能力，让学生体验学习数学的乐趣。”所以，学习数学的最终目的是学生能直接运用所学的知识和技能，以及日常生活中积累的经验，灵活合理地去解决实际生活中的数学问题。

【教学片段三】 巩固深化，促进经验向能力的转化

（课件出示当堂训练题目，学生独立完成）

1.将一个底面直径12 厘米、高1O厘米的圆柱的侧面沿其中一条高展开，得到一个（  ）形 ，它的长是（  ）厘米，宽是（  ）厘米 ，面积是（  ）平方厘米。

2.制作10节底面直径 2分米、高2米的圆柱形铁皮通风管（接头处忽略不计），至少需要多少铁皮？

教学中，教师尽可能地引入更多的具有真实意义的问题，努力为学生在生活中寻找解题的依托，让他们用生活经验解决问题，用数学知识解释生活现象，形成解决问题的基本策略，增进对数学的理解和学好数学的信心。学习数学服务生活的观念，把数学知识生活化，生活问题数学化，使数学真正为生活所用，让学生的数学思维异彩缤纷。

“数学教学是数学思维活动的教学”，让我们立足数学课堂，用抽丝剥茧的手法开展教学，帮助学生启萌直觉思维，启发形象思维，启悟逻辑思维，启迪创新思维，真正实现学生学习数学思维多元的发展。

参考文献

[1]王秀清.试论小学数学教学中学生数学思维能力的培养[J].中国校外教育，2017.

[2]宋彩红.浅谈小学数学教学中的逻辑思维方法[J].新课程学习：基础教育，2011.

[3]丁小冬.在数学教学中发展学生思维能力[J].小学科学（教师版），2019年11期.