浅谈初中数学利用建系法巧解几何题
曾钰玲
(福建省漳州实验中学 363000)
一、建系法
建系法作为函数的开端,也有一定的难度.不会建系,坐标写不清楚,中点坐标公式、两点距离公式不会应用等等的问题,都会使得一部分学生对建系法望而却步.然而仍然不能否认建系法对解题的帮助.
因此,本文挑选一些几何题,对比几何法解题和建系法解题,能更直观的理解几何法与建系法.从而加深对建系法的理解,学会使用建系法巧解几何题.
解题过程中可能会用到中点坐标公式、两点坐标公式,在此先作补充:

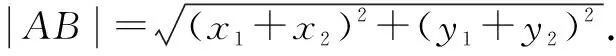
二、例题讲解
例1如图1,正方形ABCD与正方形CGEF的边长分别是2和3,且B,C,G三点在同一条直线上,M是线段AE的中点,连接MF,则MF=____.

解法一几何法
对于学生来说,几何题用几何法解,是最直接的思路,而几何法通常需要作辅助线,这就是几何法的难点所在.
解延长AD,与FM的延长线交于点Q(如图2)
因为M是线段AE的中点,所以AM=EM
又因为四边形ABCD与CGEF都是正方形,
所以AD∥EF
所以∠AQM=∠EFM,∠MAQ=∠MEF
所以△FME≌△QMA(AAS)
所以MQ=MF
因为∠FDQ=90°,FD=FC-DC=1
DQ=AQ-AD=FE-AD=1
所以△FDQ是等腰直角三角形,腰长为1

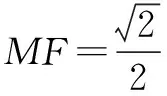
解法二建系法

思路分析要求MF的长,则需要M点坐标和F点坐标,F点坐标易知,所以只需求M点坐标即可.而M点是AE中点,所以只需知道A、E点坐标即可,A、E点坐标易知.(如图3)
解以C为坐标原点,BC所在直线为x轴,建立平面直角坐标系.则A(-2,2),E(3,3)
因为M是线段AE的中点,
因为F(0,3)
所以由两点距离公式得
从以上解题过程可以很直观看出用建系法解题相对于几何法来说,确实简单很多,书写上也更简洁.减少了学生最常出错的辅助线描述过程,减少了思考量.思路也更为直接.
建系法有时还会涉及到求函数解析式和交点坐标,也是学生非常容易出错的难点.
例2如图4,已知正方形ABCD的边长为5,E,F分别是边CD、AD的中点,BE、CF交于点P,求AP的长.
解法一几何法
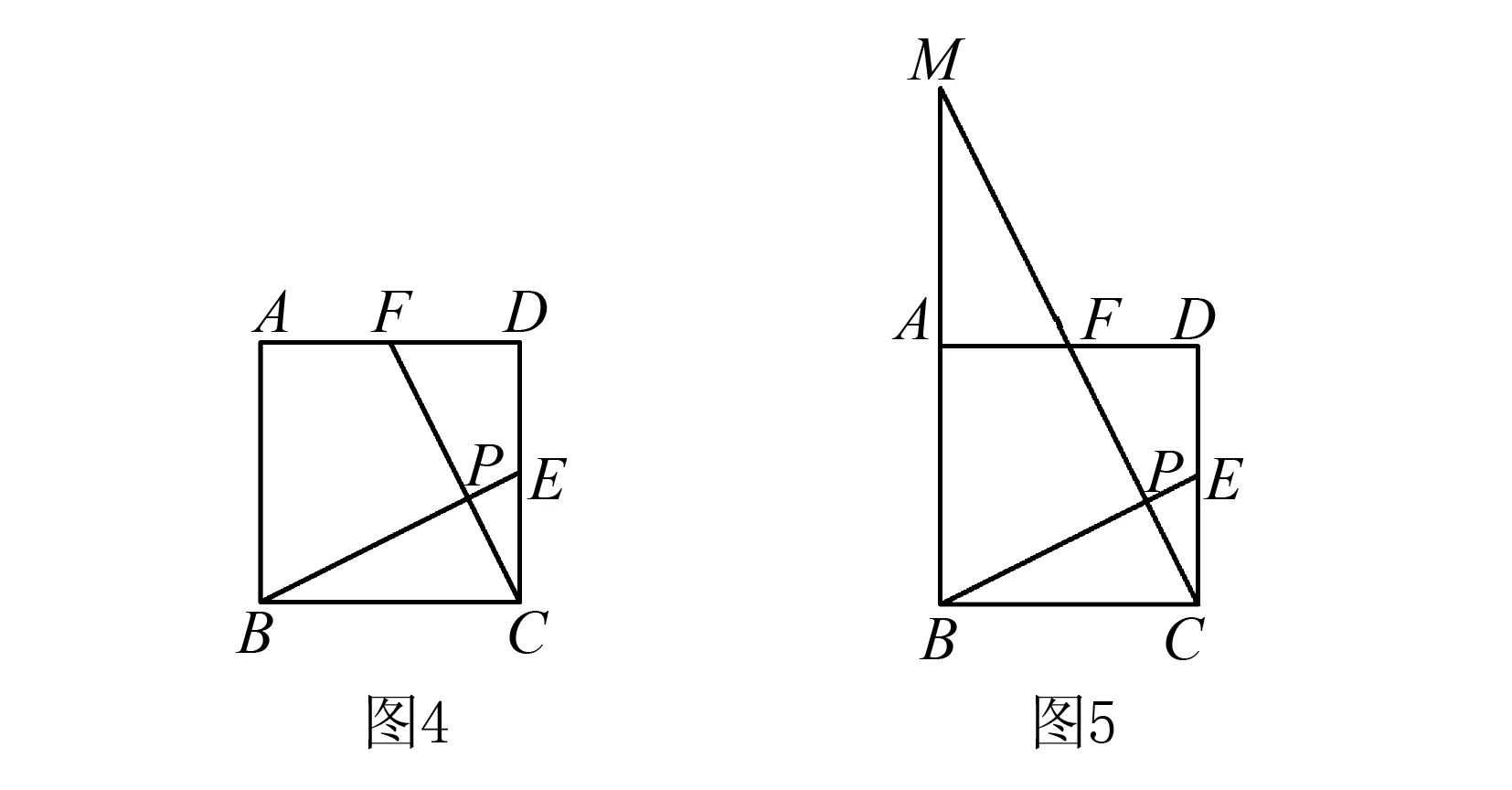
解延长PF,与BA延长线交于点M(如图5)
因为ABCD是正方形,且E,F是中点
所以△BCE≌△CDF
所以∠PBC=∠FCD
因为∠PBC+∠BEC=180°-∠BCE=90°
所以∠FCD+∠BEC=90°
所以∠EPC=90°,所以∠FPB=90°
因为F是AD中点
所以△AFM≌△DFC
所以AM=DC
所以A是BM中点
所以PA为RT△BPM中斜边BM上的中线
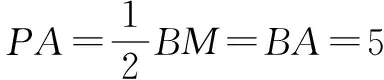
解法二建系法
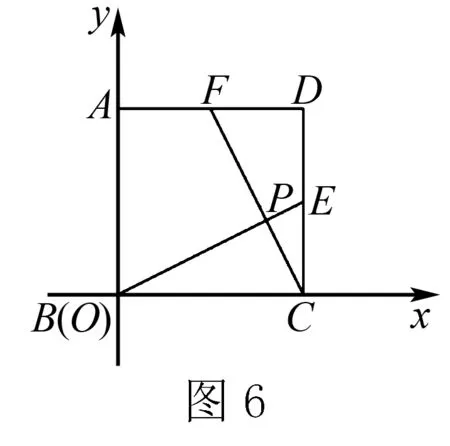
思路分析则要求AP的长,需要知道A点坐标和P点坐标,A点坐标易知,则只需求P点坐标即可.而P点是BE与CF的交点,则需要求出BE和CF所在直线的表达式即可.(如图6)
解以B为原点,BC所在直线为x轴,AB所在直线为y轴,建立平面直角坐标系.C(5,0),B(0,0)
因为E、F是CD、AD中点,所以E(5,2.5),F(2.5,5)
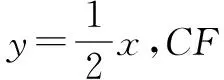
BE、CF交点坐标P为(4,2)

对比几何法与建系法会发现,几何法涉及到的知识点较多,并且不同的题目会涉及到不同的知识点,但建系法则比较单一,即使在不同的题目内,几个公式也可以反复用.
以上两个例子是在正方形的背景下,而建系法绝不仅仅能用于正方形,接下来将介绍建系法在其他题型的应用.(注:以下只展示建系解法,不再展示几何解法)
例3如图7,△ABE与△DBC都是等腰直角三角形,BC=2,AB=4,G、H分别是CD、AE中点,则GH=____.
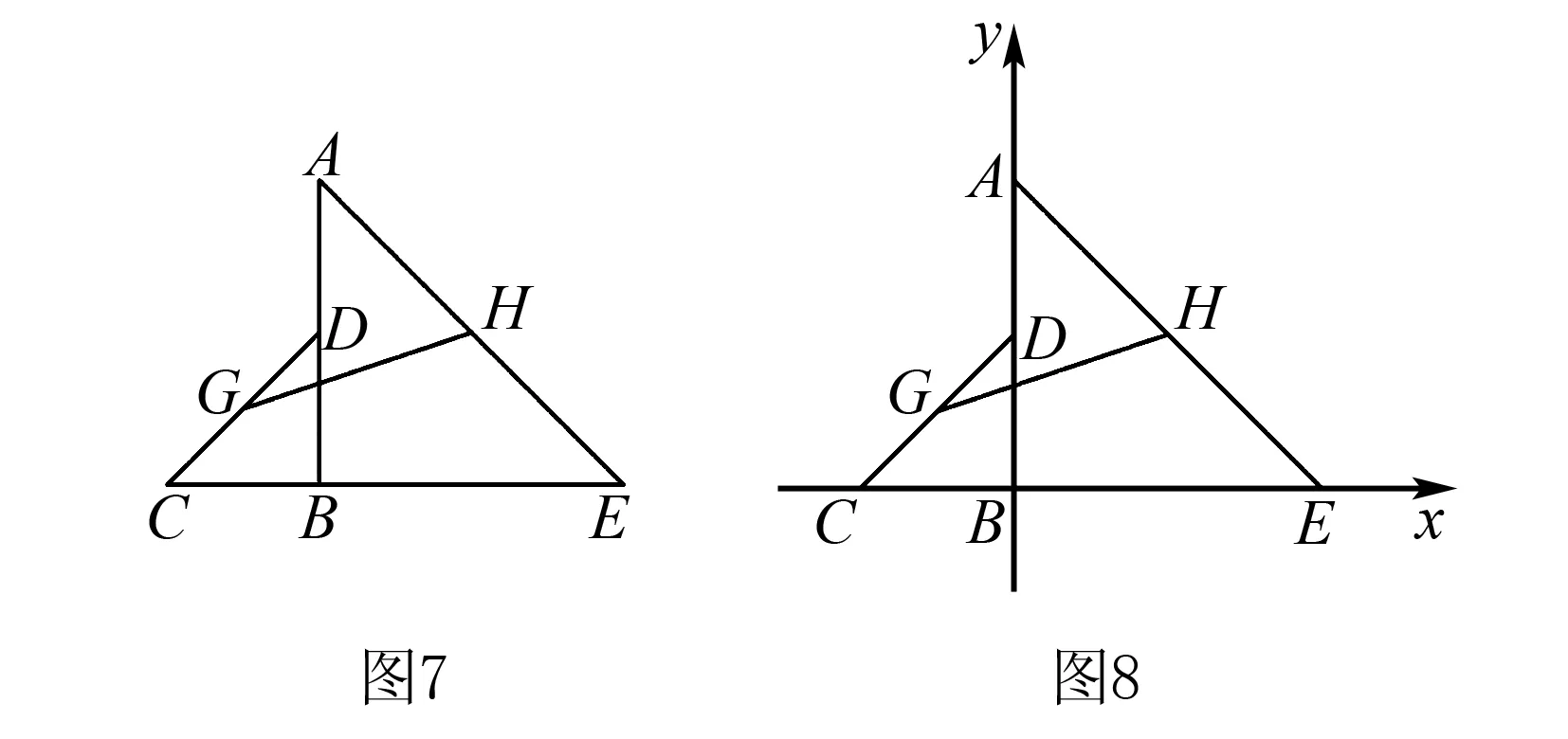
思路分析要求GH的长,需要G、H两点坐标,G、H是CD、AE中点,A、E、C、D坐标易知,因此此题用建系法做非常简单.
解以B为原点,BE为x轴,AB为y轴,建立平面直角坐标系(如图8)A(0,4),E(4,0),C(-2,0),D(0,2)
所以G(-1,1),H(2,2)

从解题思路及计算过程均可看出,用建系法解几何题,难度下降.因此平时上课时,老师也可以有意识的引导学生用建系法解决较难的几何题.
总结数学本身是一门思维非常灵活的学科,如何在数学的学习过程中提高学生对数学概念的理解,促进发散性思维的提升,从而形成良好的认知结构,是作为一线数学教师需要不断学习的一种能力.
对于初中学生来说,函数是一个难点,但是如果函数学好了,也能成为一把利剑,帮助学生提高解题能力.本文只研究了平面直角坐标系对解决平面几何问题的帮助,而高中阶段,空间直角坐标系对于立体几何的帮助也是很大的.并且,建系法不仅在解几何题方面有帮助,在提高学生数形结合能力方面的帮助更大.作为一线教师,平常的解题过程可以多向学生灌输建系法,让学生在多次练习中熟悉,并且掌握建系法,最终实现能用建系法解题的目的.

