浅谈分析法和综合法在解三角形题目中的应用

李 蕾

(云南省昆明市云南师范大学数学学院 650500)

解三角形在高考中常与三角函数、三角恒等变换或平面几何等结合考察，分值为5到14分不等.对近几年相关高考题的统计分析，发现该模块内容年年必考且解答题出题频率有所增加.通过某市期末联考数据统计可知学生该模块的得分较低，不少研究者也指出学生在该模块的高考题中得分并不佳，说明学生该模块解题方面存在问题.

解题的首要步骤就是审题，这需要学生掌握一定的审题技巧，能够充分挖掘已知条件并在问题与已知之间搭建桥梁.解题教学不仅要注重题目解答知识层面的讲解，同样应该注重教会学生如何思维，做到知识与方法层面的统一，培养学生分析、解决问题的能力.分析法与综合法作为常见的思维方法，解题时有效运用可为学生指明解题方向.下面将简要进行介绍.

一、分析法与综合法概述

如果从题设的已知条件出发，运用一系列有关已确定的命题作为推理的依据，逐步推演而得到要证明的结论，这种证明方法叫综合法；如果推理方向中由命题判断向题设方向，论证中步步寻求使其成立的充分条件或已经成立的事实，这种证明方法叫分析法.

实际应用中常将二者结合使用.综合法往往可以导出较多命题，但具体哪个可得出结论有时不易看出，此时结合分析法可快速锁定解题方向，与问题之间搭建桥梁.在一些证明中常用分析法寻找思路，用综合法写出具体的过程，二者相互联系，不可分割.两种方法的结合使用有利于学生解题能力及逻辑推理素养的提升.

二、分析法与综合法在解三角形高考题中的应用

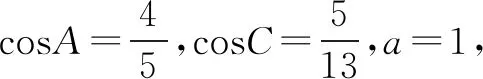
分析这道题看起来不难，解法也不唯一.但如果方法选取不当，可能导致运算量太大，学生算不出来.不少学生解题时看到对边及对角的余弦值时认为选用余弦定理求解边b，基于该思路先结合已知求出角A、C的正弦值，然后利用正弦定理求出边c,之后选取相应的余弦定理公式，结果得到了一个计算量很大的一元二次方程，导致无法计算.这种解题过程显然没有错误，但实际计算中却遇到了阻碍，这时又没想着更换策略.笔者认为在实际教学中引导学生运用分析法与综合法分析题目可帮助打开学生思维，突破解题困境.为此，我们可引导学生进行如下分析：

1.知道△ABC的内角A,B,C，则可以知道A+B+C=π.

2.知道cosA，便可以知道sinA；如果知道cosC，便可以知道sinC等.(一级推导)

3.知道了cosA、sinA、cosC、sinC，可以知道sin(A±C)或cos(A±C)等.(二级推导)

4.知道了A+B+C=π及sin(A±C)等，结合诱导公式可知道sinB等

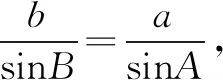
具体解答步骤如下

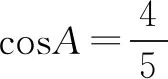
例2(2020全国Ⅰ文数)△ABC的内角A,B,C的对边分别为a,b,c.已知B=150°，

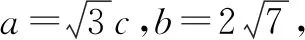
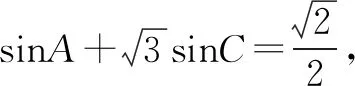
分析这道高考题对于刚学习过解三角形内容的学生还是有难度的，学生常常不知如何思考.解题中可引导学生用综合法及分析法分析更有利于掌握其中的转化思想.

1.综合法：题设已知角B，从角B自身可以知道sinB、cosB等(一级推导)；知道了sinB，题设中给的是在三角形中，那么知道角B，可以知道A+C(二级推导)；就可以知道sin(A+C)等.

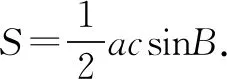
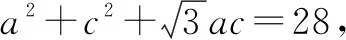
4.分析法：对于(2)仅知道一个关于角A与角C的关系式及角B，要求角C.不能求出角A就将其转化.

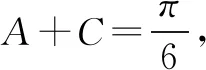
具体解答步骤如下

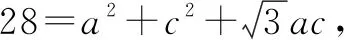
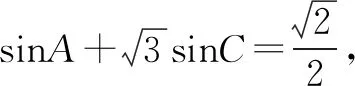
例3(2014安徽卷)设△ABC的内角A,B,C的对边分别为a,b,c,且b=3，c=1，A=2B.

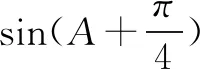
分析这道高考题看着很简练，但学生很容易卡在第(1)问.学生可能会经历直接应用正弦或余弦定理的试错过程，发现无法求解后不知所措.此时学生若能灵活运用分析法思考，第(1)问就比较容易解决.学生可以想到需要知道的是边a，但不管是直接运用正弦定理还是余弦定理都会有新的未知量，无法解决.要运用正余弦定理必须要知道角A的正余弦值,那么题目中与边a密切相关的是角A,题目中只是角A的一个关系式无法直接知道其正弦值等，要想用需要出现正弦或余弦，所以想着构造出sinA=sin2B，接下来通过边角互化进一步化简变形，题目思路就明确了.

具体解答步骤如下

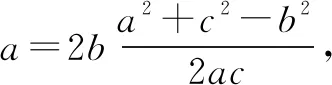
利用综合法推导时不仅要注意每个条件可直接推出的结论，还要将条件组合看能否进行二级推导.推导出的信息越全面越有利于快速理清思路.可行路径多样时将二者结合使用可快速锁定方向减少盲目尝试,同时可培养学生的思维能力.分析题目作为解题的第一步，教师在解题教学时应特别重视教会学生分析的方法，做到授之以“渔”.