已知函数的最值求参数的值或范围问题的求解策略
李文东
(广东省中山市中山纪念中学 528454)
已知函数f(x)在区间[a,b]上的最值,求参数的值或取值范围,这类问题高考常考的问题,其一般解法是对参数进行分类讨论得到函数f(x)的单调性,解法较为复杂.根据函数最值的定义(以最大值为例):函数f(x)在区间[a,b]的最大值为M,即对任意的x∈[a,b],f(x)≤M,且存在x0∈[a,b],使得f(x0)=M.因此函数的最值问题其本质是一个函数恒成立问题,我们可以按照函数恒成立问题的思路对函数的最值问题进行求解.经笔者研究发现,此类问题有如下求解策略.
一、分类讨论函数的单调性
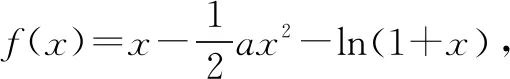
(1)若x=2是f(x)的极值点,求a的值;
(2)若f(x)在[0,+∞)上的最大值是0,求a的取值范围.
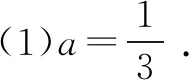
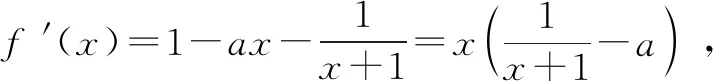
①当a≤0时,f(x)在(0,+∞)上单调递增,由f(0)=0,知不合题意.
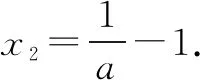
当0 当a=1时,f(x)的单调减区间是(-1,+∞). 当a>1时,-1 当a≥1时,f(x)在(0,+∞)单调递减,可得f(x)在[0,+∞)上的最大值是f(0)=0,符合题意. 所以f(x)在[0,+∞)上的最大值是0时,a的取值范围是[1,+∞). 点评分类讨论是解决已知最值求参数或参数范围问题的基本方法,但是这种解法相对比较繁琐. 例2设函数f(x)=2lnx+x2-2ax,若f(x)在区间[1,2]上的最小值为0,求实数a的值. 点评当x∈[a,b]时,fmin(x)=m,我们可以取特殊值x0∈[a,b],则f(x0)≥m,充分利用这一必要条件来缩小参数a的取值范围,从而可以减少讨论的情况,当然这种解法极大的依赖参数a的取值范围能缩小到什么程度. 点评已知函数f(x)在区间[a,b]上的最小值(最大值)为m(M),若通过观察发现x0∈[a,b],使得f(x0)=m(f(x0)=M)成立,则必有f′(x0)=0,然后验证充分性即可. 解注意到f(0)=1,从而x=0应为f(x)的极值点,由于f′(x)=ex-kx-1,可知f′(0)=0显然成立.要使当x≥0时f(x)的最小值为1,则必存在x0>0,当x∈(0,x0)时,f(x)单调递增,也即当x∈(0,x0)时有:f′(x)≥0,由于f′(0)=0,同理必存在x1>0,当x∈(0,x1)时,f′(x)单调递增,也即当x∈(0,x1)时有:f″(x)≥0,从而f″(0)=1-k≥0,得k≤1,而当k≤1时,f′(x)=ex-kx-1≥ex-x-1≥0,即f(x)在[0,+∞)上递增,故fmin(x)=f(0)=1. 点评对于∀x∈[a,b],f(x)≥m,若f(a)=m,利用端点处导数值满足f′(m)≥0这一必要条件得出参数的范围,然后说明这一范围的充分性.这是端点效应. 例5已知函数f(x)=lnx+ax2+bx(a≠0)在x=1处取得极值. (1)当a=1时,求f(x)的单调区间; (2)若f(x)在(0,e]上的最大值为1,求a的值. 解(1)略 点评已知函数f(x)在区间[a,b]上的最小值(最大值)为m(M),即对于任意的x∈[a,b],有f(x)≥m(f(x)≤M)成立,且存在x0∈[a,b],使得f(x0)=m(f(x0)=M)成立.将不等式f(x)≥m(f(x)≤M)分离参数得a≤g(x)(≥g(x)),则a=gmin(x)(gmax(x)),这样可以完全避免分类讨论,这是解决这类问题的一个很好的办法. 具体解题中对于以上方法的选择,我们可以先通过观察函数f(x)的结构特点,看看是否满足策略2中的一些条件,如果不满足,则我们可以尝试采用策略3的方法,当然如果策略3中不容易分离参数或者分离后得到的函数很复杂,则我们也可以考虑直接求导分类讨论来求解.
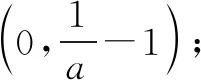
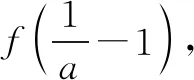

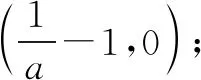
二、利用必要条件缩小参数范围,减少分类讨论
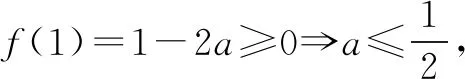
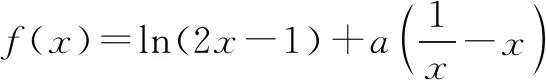
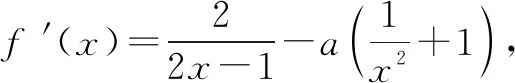
三、分离参数