数列中的最值问题
张 庆
(江苏省徐州市侯集高级中学 221000)
在解决数列中,我们经常会碰到数列的通项、求和、项数、应用等的最大值与最小值问题.通过题目中给出的相关信息,结合相关的数列定义、性质以及相关公式,来解决相应的最大值或最小值问题,是函数性质的一种特殊表现.下面结合几类常见的数列中的最值问题加以实例剖析.
一、通项an的最值问题
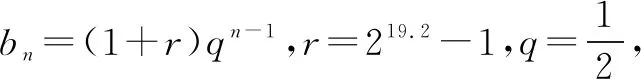
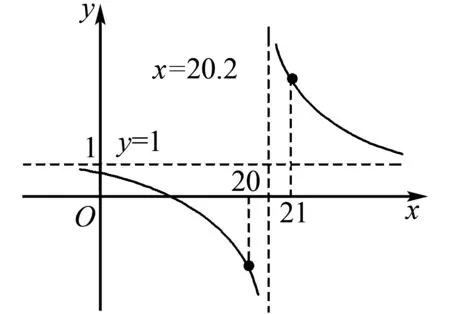
图1
分析根据数列的通项结合对数运算加以变形,根据相应的函数的图象来确定通项中的最大值与最小值问题.
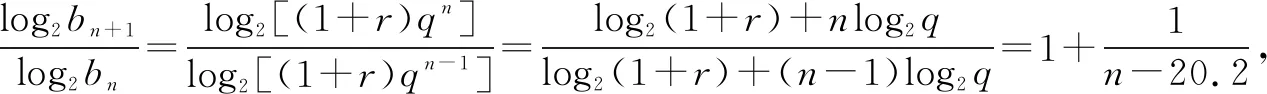
易知:c20
点评:本题通过通项公式的转化与变形,利用构造相应的函数的图象与性质加以数形结合,考查对数运算、数列的通项与函数的图象问题.数列是一类特殊的函数,其对应的通项的最值问题相当于对应的函数中的自变量的最值问题,经常把数列问题函数化来处理.
二、和式Sn的最值问题
例2 设等差数列{an}的前n项和为Sn,已知a1>0,S12>0,S13<0,指出S1,S2,…,S12中哪一个值最大,并说明理由?
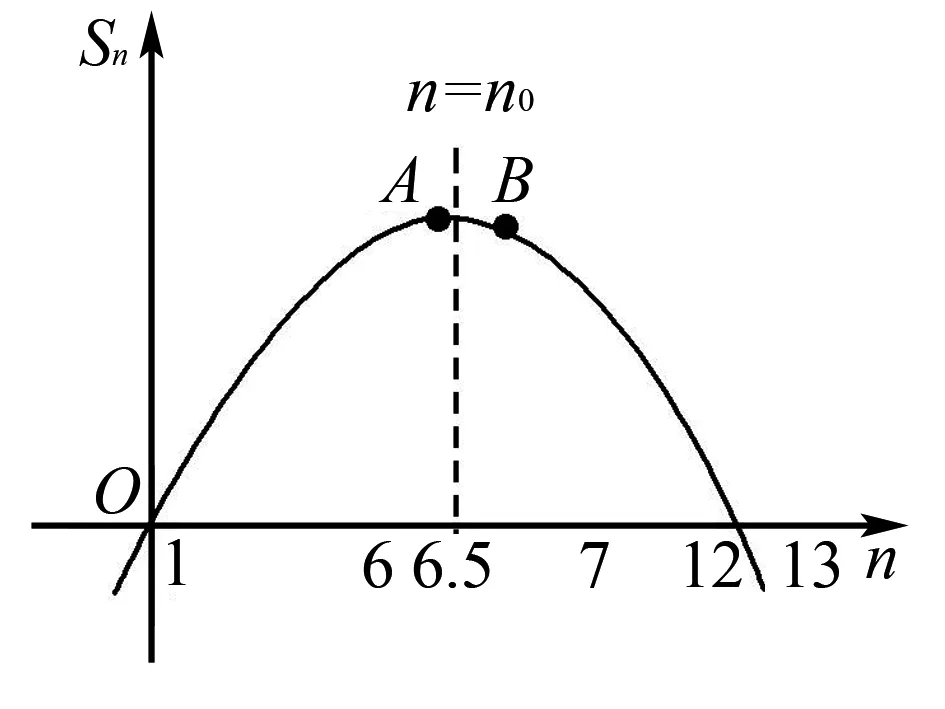
图2
分析通过等差数列的前n项和为Sn的关系式与对应的二次函数图象的性质,结合参数n的取值的限制条件来确定Sn的最值问题.
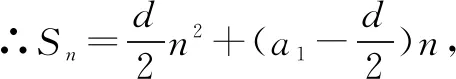
∵S12>0,S13<0,∴a13=S13-S12<0,∵a1>0,a13<0,∴d<0,
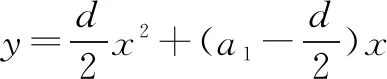
∵S12>0,S13<0,∴12<2n0<13,∴6 易知n=6对应的A点(6,S6)与对称轴的距离比n=7对应的B点(7,S7)与对称轴的距离更小,∴A点为最高点,S6最大. 点评:本题结合等差数列的前n项和公式,二次函数的图象与性质,考查数形结合思想以及运算能力等.通过把求和公式转化为相应的二次函数的解析式问题,利用二次函数的图象与性质来确定Sn的最值问题. 例3设数列{an}(n=1,2,3,…)的前n项和Sn=2an-a1,且a1,a2+1,a3成等差数列. (1)求数列{an}的通项公式; 分析(1)利用数列的前n项和Sn与an间的关系,结合等比数列的定义来确定数列的类型,并结合条件建立关系式求解a1的值,进而求解相应的通项公式;(2)通过等比数列求和,结合绝对值不等式的求解来确定参数的最值问题. 解析(1)由已知Sn=2an-a1,有an=Sn-Sn-1=2an-2an-1(n>1),即an=2an-1(n>1),从而a2=2a1,a3=2a2=4a1,又因为a1,a2+1,a3成等差数列,即a1+a3=2(a2+1),所以a1+4a1=2(2a1+1),解得a1=2,所以数列{an}是首项为2,公比为2的等比数列,故an=2n; 点评本题主要考查等差数列与等比数列的概念、等比数列通项公式与前n项和公式等基础知识,考查运算求解能力等.解决本题的关键是通过转化与化归思维,把求和型的数列最值问题转化为不等式的求解问题,结合项数n的取值情况加以相应的最值问题. 例4某住宅小区计划植树不少于100棵,若第一天植2棵,以后每天植树的棵树是前一天的2倍,则需要的最少天数n(n∈N*)等于. 分析根据实际应用问题确定对应的数列为等比数列,再结合等比数列的求和公式,通过建立相应的不等式来分析与求解最值问题. 点评利用数列知识来解决实际应用问题中的最值时,要注意结合特殊数列的定义、通项、性质、求和公式等加以转化,特别对于求解相关的参数问题,一定要结合实际应用问题,确定在正整数范围的n的取值情况. 例5 若一个数列的第m项等于这个数列的前m项的乘积Tm,则称该数列为“m积数列”.若各项均为正数的等比数列{an}是一个“2020积数列”,且a1>1,则该数列中Tn取得最大值时n的值为____. 分析用创新定义建立数列的关系式,进而求得a1010=1,利用a1>1,得到公比0 解析由题中的创新定义可知a1a2a3·…·a2020=a2020,故a1a2a3·…·a2019=1,由于{an}是各项均为正数的等比数列且a1>1,所以a10102019=1,即a1010=1,而a1>1,则有a1010=a1q1009=1,可知公比0 点评本题在创新定义下建立等比数列关系式,通过等比数列的通项与性质来分析与求解,关键是理解创新定义与对应关系式的建立,进而结合等比数列的对应性质加以分析与应用. 抓住数列的定义、通项、求和以及性质等,合理应用数列的函数性质,解决一些涉及数列的最值问题,有效融合数列与函数之间的交汇,很好考查数学知识、数学思想方法和数学能力,提升数学品质,培养数学核心素养.三、项数n的最值问题
四、应用中的最值问题
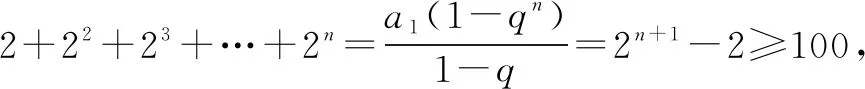
五、创新中的最值问题

