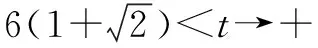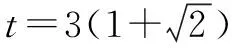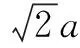巧用分类思想来解决面积重合问题

侯坤明

(江苏省灌云实验中学 222200)

几何图形的运动变化问题一直以来都是中考命题专家青睐的热点，这一类题目在编写时都不同程度上体现出基本图形、基本概念来源于现实生活，将现实生活中的一些问题抽象化得到.这类题型注重培养学生良好的观察、操作、想象、讨论、交流等学习习惯，学生在吸收知识的同时更能够领悟其中蕴含的基本数学思想，并通过适度的提炼和总结，使之能对认识能力、理解能力和应用能力起到指导作用，更好的理解数学实质，初步获得数学思维能力.

笔者在给学生讲解苏教版八年级下学期第95页的第22题时，受到了一些启发.原题如下：

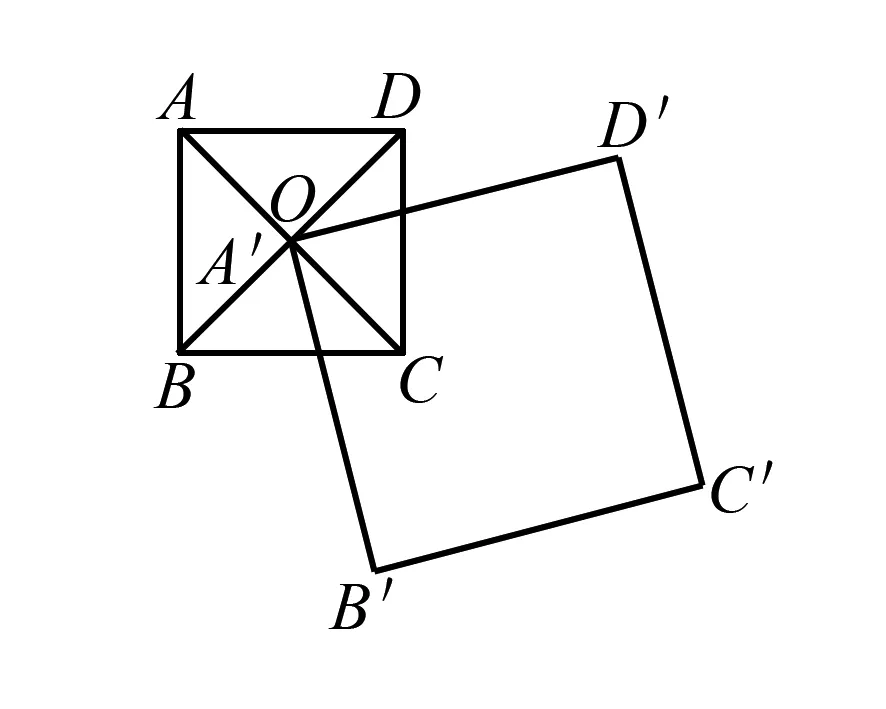
图1

如图1，正方形ABCD的对角线AC、BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，将正方形A′B′C′D′绕点A′旋转，在这个过程中，这两个正方形重合部分的面积会发生变化吗？证明你的结论.

我们将上题中的两个正方形都变为：

边长为6的相同正方形，按如图2所示方式放置，右边正方形EFGH是水平放置的，其中∠BCF=45°,C是EF的中点(左边正方形的右边顶点与右边正方形的边所在的中点重合)，同时令左边正方形水平向右按每秒钟一个单位长度平移，右边正方形EFGH固定不动.请你尝试解决以下问题：

(1)在运动过程中BC与FG的夹角等于____度；

(2)当t=2时，求正方形ABCD余下的面积；

(3)请你计算从左边正方形ABCD开始进入直至完全穿过并离开右边正方形EFGH时，两正方形重合部分的面积s与运动时间t(初始状态时t=0秒)之间的函数关系,并求出对应的t的取值范围.

(4)在(3)的情况下有无重合面积的最大值，若有请求出来；若没有，请说明理由.

解(1)45°(135°)；(2)32；(3)(ⅰ)分析：首先呈现移动变化过程中的关键位置的系列图，然后根据重合部分形成的多边形的边数划分为八种不同的情况.每一种情况分别分为两个状态图，即进行状态和结束时的临界状态，并分别计算此种情况下它们重合部分的面积与运动时间t(初始状态时t=0秒)之间的函数关系.

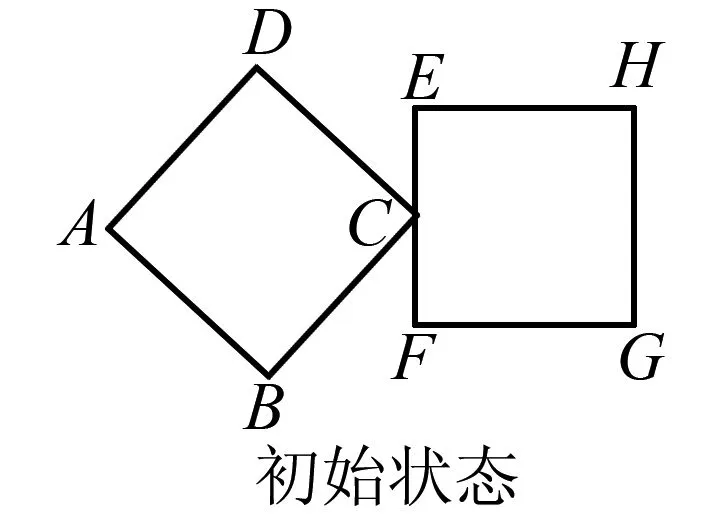
图2

(ⅱ)解答如下：

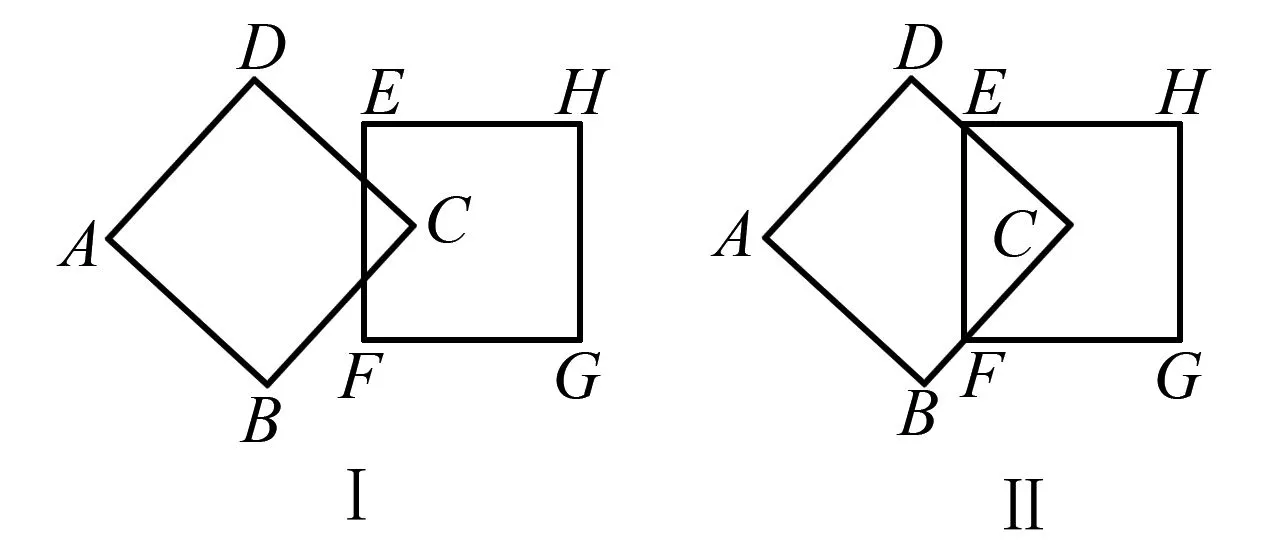
图3

第一种情况：

0≤t≤3,s1=t2;

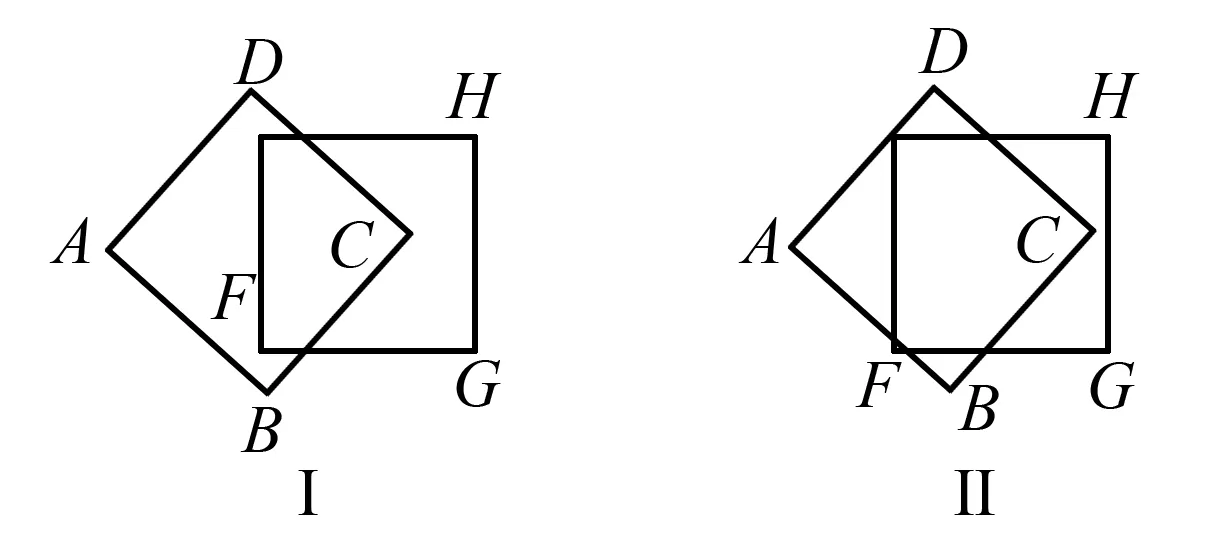
图4

第二种情况：

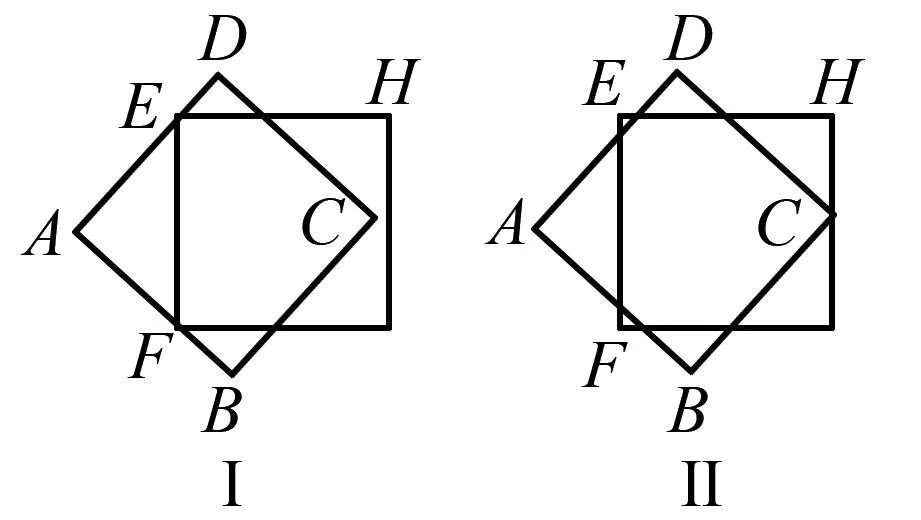
图5

第三种情况：

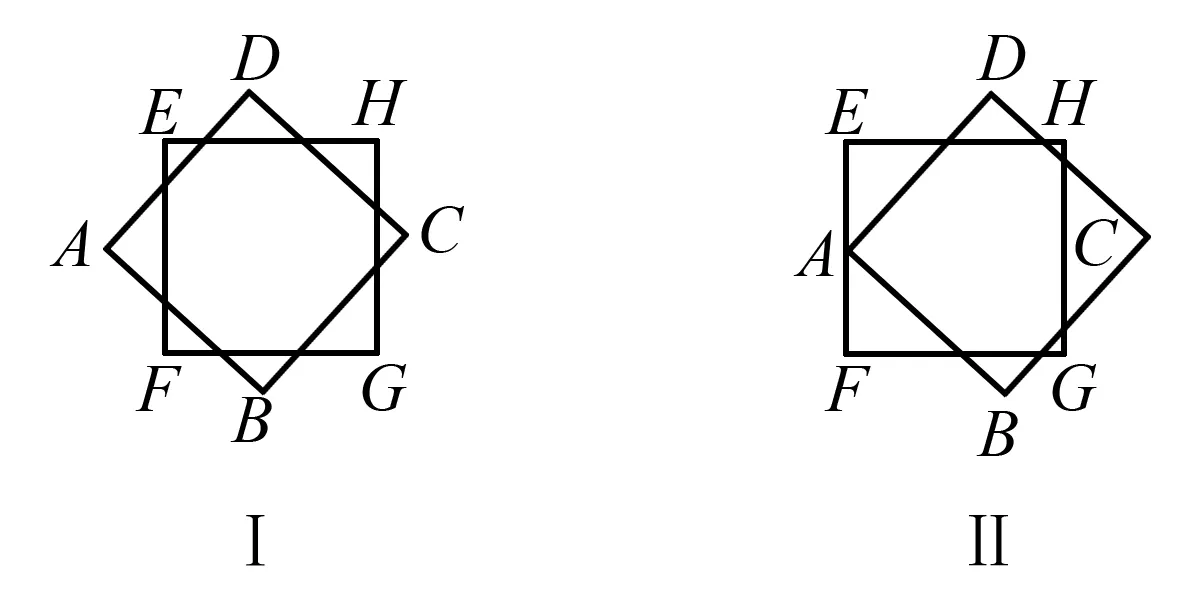
图6

第四种情况：

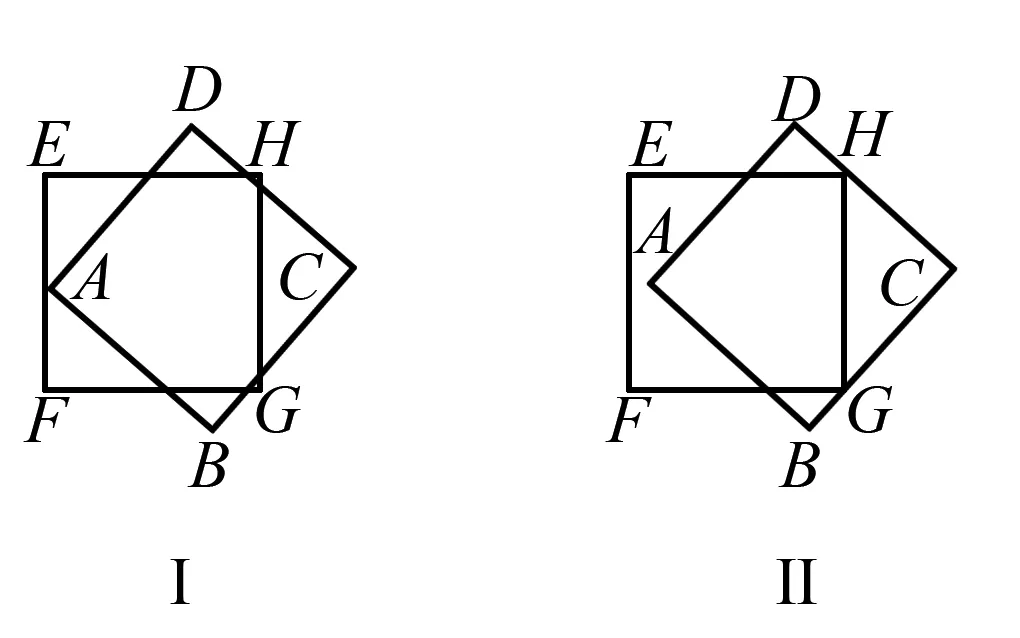
图7

第五种情况：

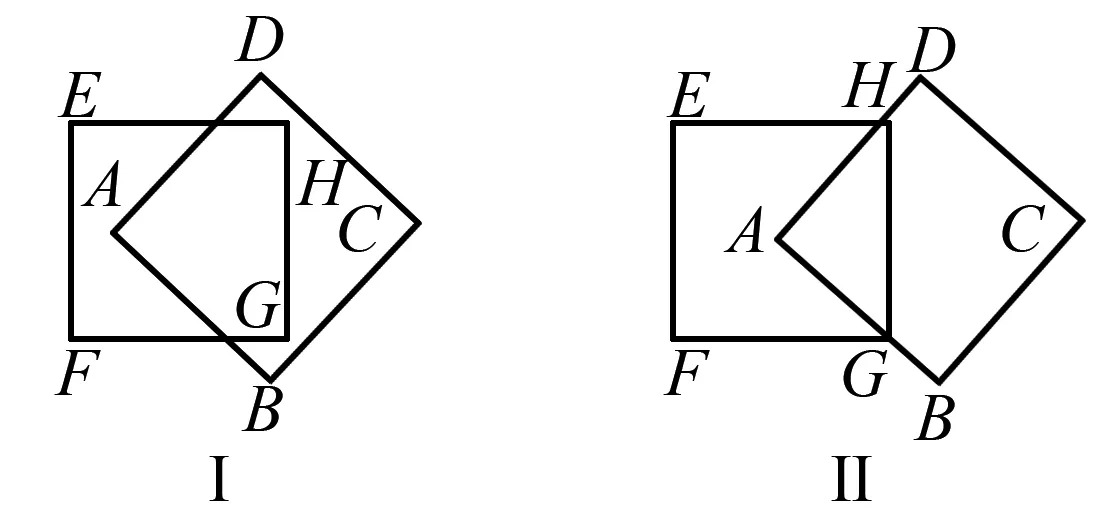
图8

第六种情况：

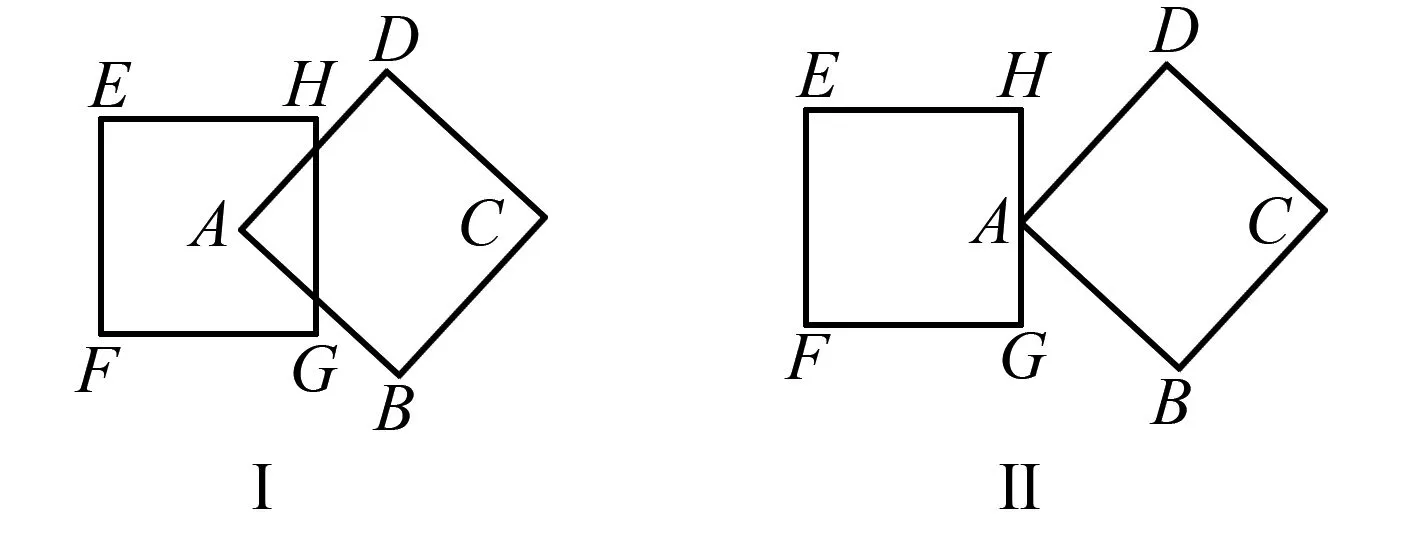
图9

第七种情况：

图10

第八种情况：