例谈体现数学文化的初中数学教学

杨赛萍

(福建省莆田市城厢区南门学校 351100)

数学文化教育是我国新课程标准中的重要组成部分，也是推行素质教育的重要基础，在学习基础知识的基础上，让学生得到能力与思维的提升.因此，在教学中，教师应肯定数学文化的教学价值，为学生提供时间与空间充分进行数学文化的学习.

一、数学文化实践性的体现

在数学教学研究和实际教学中发现学生在数学学习中对于贴近于生活、社会的习题更具有学习的欲望.例如，在学习轴对称、中心对称的知识时，教师可结合我国传统文化中剪纸文化，组织学生一同进行剪纸活动，进行数学知识的教学.例如，生活中十分具有历史意义的中国象棋，是学生所感兴趣的，因此将教学中运用生活中的棋艺活动，进行有序实数对知识的学习，运用棋盘中棋子的变化，理解有序实数对的含义.

例1 如图1，在一个棋盘中，如果假设其中“帅”的位置为(-3,-5)，“士”的位置是(-2,2)，请问其中“将”的位置坐标是什么？

分析：通过其中“帅”与“士”的位置，推导出其中原点的位置，在运用原点的位置即可推导出“将”的位置.

解其中由于“帅”的位置为(-3,-5)，“士”的位置是(-2,2)，所以其中原点的位置处于“马”的位置，因此可以解得其中“将”的位置为(-3,3).

评价学生通过具有文化气息的“象棋”这一实际案例，学习有序实数对的知识，会有效增强知识的趣味性，并将原本抽象的知识更加具象化.

二、数学文化传承性的体现

算数知识在我国的古代时期就已经存在，当时的人们主要运用一种称之为“算”的竹制器具，作最为计算器具，帮助人们进行计算，因此人们将这种技术统称为算术，同时，随着不断的发展，对于与计算相关的知识也被称之为算术.并且算术知识在我国的春秋战国时期就已经取得了较为广泛的运用.在初中一次函数教学中，教师所准备的习题中鸡兔同笼的相关问题，在我国古代的《孙子算经》中就有相似的问题，被称之为“物不知数”问题，在书中对于这一问题的描述如下.

例2 鸡兔同笼，数之，有头三十五，足九十四，则鸡兔各有几何？

分析习题分析，首先是对题目的理解，将兔子与小鸡关在同一个笼子中，通过细细的查点发现笼子中有三十五个头，对于动物的脚也进行查点，共有九十四只脚，则在这个笼子中兔子和鸡的数目分别是多少.

解在《孙子算经》中，所运用的解题方法是，假设其中的所有的鸡兔都使用一只脚进行站立，因此，这时脚的数目与头的数目相同为三十五.已知当兔子四只脚和鸡两只脚时，一共有九十四只脚，所以当兔子两只脚和鸡一只脚时，共有四十七只脚.多出来的脚都是兔子的，并且每一只兔子多出一只脚，且多出脚的数目与兔子的数目相同，因此可的出兔子的数目为十二，因此鸡的数目为二十三.

评价通过对于鸡兔同笼问题的分析，可发现，我国在古代时期对于数学的理解已经达到很高的水平.因此，在初中数学教学中，教师结合的数学历史知识，可有效提高学生的学习兴趣，如在上一鸡兔同笼问题，就可运用在讲解一次函数的学习中，提高学生的学习欲望.

三、数学文化趣味性的体现

将教学融入学生所喜欢的情境中，在提高数学教学质量的基础上，达到更吸引学生的学习效果.

例3 如图2所示的一个圆锥形谷堆中，将其中顶点设为P点，有一只猫咪正好处于P点，并且在谷堆的底部圆周中有一个A点，在A点有一只老鼠.小猫发现老鼠的存在，并且准备进行捕捉，猫咪准备沿着PA这一直线向下去抓捕老鼠，但是当猫咪到达A点时，发现老鼠已将察觉，并且绕着圆周开始逃跑，猫咪紧紧跟随，终于在B点处，成功捕捉老鼠，并在捕捉到老鼠后，沿着PB这一母线返回P点.假设其中猫咪的速度都是匀速，顶点P与猫咪的距离为s，从开始捕捉老鼠并成功返回所运用的时间为t，请运用函数关系图像表示在s与t之间所具有的函数关系.

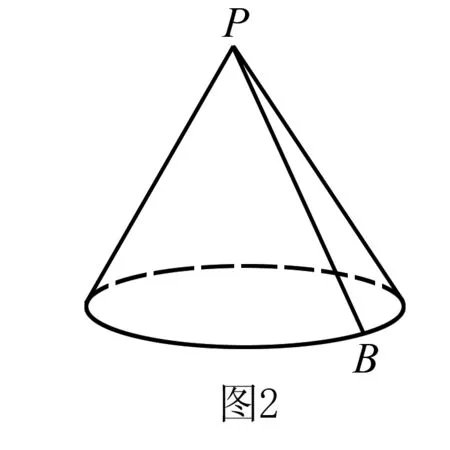
分析在猫咪沿PA直线到达圆周的过程中，猫咪一直是匀速，并且逐渐与顶点的距离变大，因此这一时间，距离随着时间的增大而增大.但是当猫咪在追赶老鼠时，由于一直处于圆周处，因此s一直都没有发生变化.而当猫咪返回P点时，与顶点之间的距离逐渐减小，因此s随着时间t的增大而减少.

解猫咪从P点到A点时，s随着t的增大而增大，因此是一条斜上的直线.

当猫咪在圆周进行奔跑时，s不发生变化，因此是一条平行x轴的直线.

当猫咪从B点返回到P点时，s随着t的增大而减少，因此是一条斜下的直线.

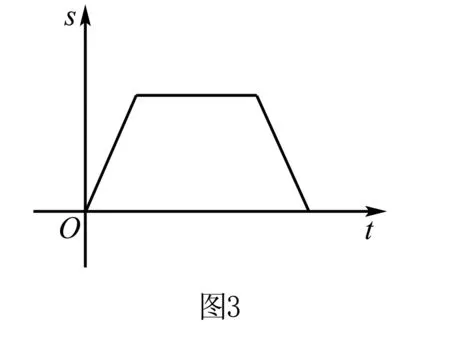
结果如图3.

评价这一习题中，教师运用“猫与老鼠”这一情景，带领学生走进数学课堂中，并在这种趣味性中学习理解函数图像知识，建立对其真正的认知，从而获取更深层次的理解.

四、数学文化艺术性的体现

数学中所具有的形体美，在学习轴对称、中心对称等知识时，都有很深刻的体现，并且在课外拓展中，数学比例美着重体现在黄金分割这一知识中，利用数学文化的美感与知识的相融合，激发学生学习的欲望与探索精神.

例4 在吉他弹奏中，不同的琴弦长度与绷紧力度会决定不同的音色，比如，在相同力度下，运用长度成比例的琴弦，如长度比为15:12:10，进行敲击，会发出do、mi、so这三个调和的乐音.但是在对于比例中数字的倒数进行分析时，发现这样一个规律.

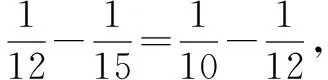
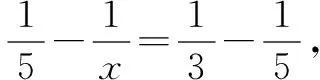
评价通过发现生活中所蕴含的数学美，与数学问题相结合，从而为学生展示数学的美感，并体会数学的实用性.

五、数学文化实用性的体现

数学的知识来源于生活，因此也必须用之于生活.在但是实际教学，依然只是单纯的建立起生活与数学知识之间的联系，缺乏知识在生活中的充分运用.

例5 在汶川地震发生后，北京市政府紧急进行准备，支援地震地区的救援工作，在前往中，为地震地区提供5600m2的板材与2210m的铝材，主要用于灾区搭建临时安置点，主要搭建以下两种样板房，其中根据搭建的要求，请问应该怎样进行材料的调动.

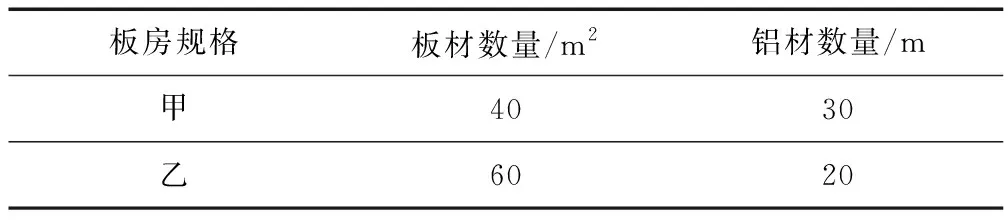
板房规格板材数量/m2铝材数量/m甲4030乙6020

分析运用所学习的知识，假设所需要构建的甲板房为x间，通过题目可知，构建的乙板房为100-x间，通过列不等式即可解决问题.

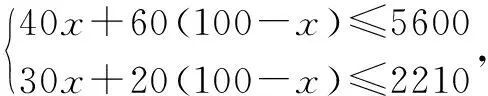
方案1：在100个安置点中，搭建20个甲板房和80个乙板房

方案2：在100个安置点中，搭建21个甲板房和79个乙板房.

评价这是一个以实际案例设计的数学问题，可结合数学学习中的一元一次不等式方程组知识.进行解决这一问题对于学生了解现实生活具有积极的促进作用，并对数学文化实用性也具有确实的体现.

数学命题是实现数学文化体现的重要途径之一.教师在教学过程中，必须充分领会数学文化所具有的五种层次特点，即实践性、传承性、趣味性、艺术性和实用性，将数学文化与命题相结合，使学生在思维与能力上得到综合性的提升，建立高效的课堂学习.