类正弦定理猜想的否定

甘志国

(北京丰台二中 100071)

笔者在文[1]中提出了如下猜想：

类正弦定理猜想在△ABC中，若满足下列条件之一，则A=B=C：

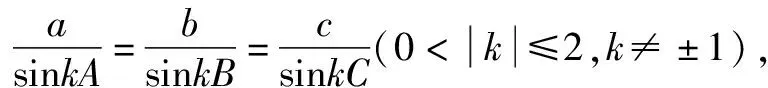
下面的定理3，4，5,6,7(其证明只用到了三角函数的恒等变形)分别否定了类正弦定理猜想的(1)(2)(3).

证明由题设及三角形内角和定理、正弦定理，可得

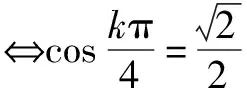
⟺k=8n±1(|n|∈N*).

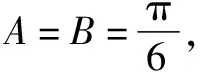
证明由题设及三角形内角和定理，得

=0(k≠1.5n,n∈Z)

⟺k=12n±1(n∈Z)

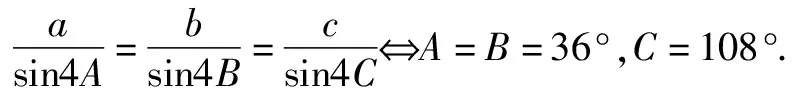
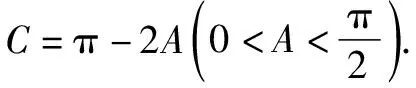
由正弦定理，可得

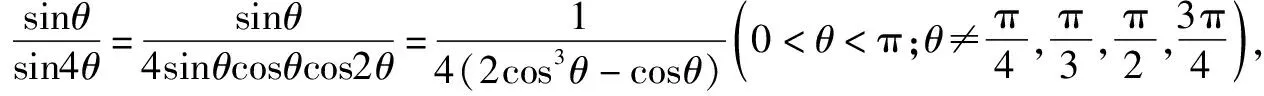
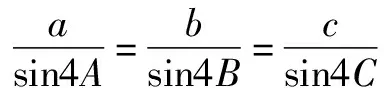
⟺2cos3A-cosA=2cos3C-cosC

⟺2cos3A-cosA=2cos3(π-2A)-cos(π-2A)

⟺2cos3A-cosA=-2(2cos2A-1)3+(2cos2A-1)

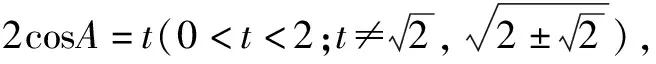
所以欲证结论成立.

证明由题设及三角形内角和定理、正弦定理，可得

进而可得欲证结论成立.

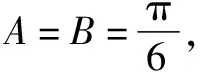
证明由题设及三角形内角和定理、正弦定理，可得

进而可得欲证结论成立.

以上研究可能离高中数学教学有点远，但下面的三道原创题是适合有兴趣的高中师生练习的.

题1在△ABC中，角A,B,C的对边分别是a,b,c.

(1)请选择下面的一个条件，证明A=B=C.

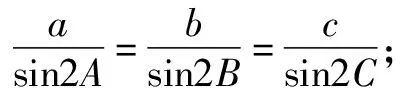
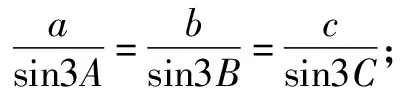
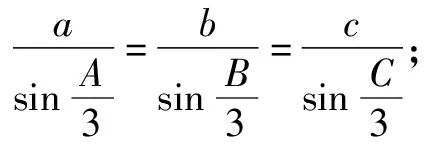
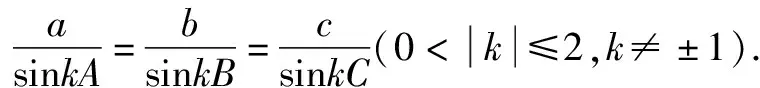
题2在△ABC中，角A,B,C的对边分别是a,b,c.

(1)请选择下面的一个条件，证明A=B=C.

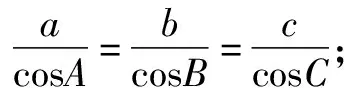
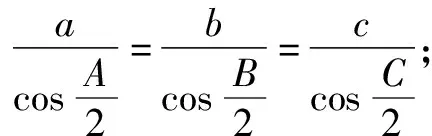
题3在△ABC中，角A,B,C的对边分别是a,b,c.

(1)请选择下面的一个条件，证明A=B=C.

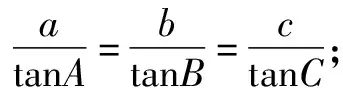
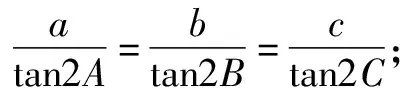
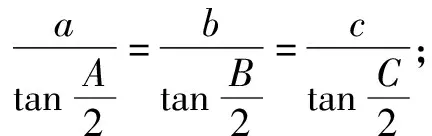
题1的参考答案(1)见文[1]中对开头题目的解答及定理1[1]的证明.

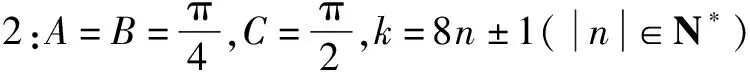
题2的参考答案(1)见文[1]中对开头题目的解答.

题3的参考答案(1)见文[1]中对开头题目的解答及定理2的证明.