解析圆锥曲线中点弦问题的几种策略

李 蕊

(甘肃省青海油田第一中学 736202)

一、策略分析

基于圆锥曲线中点弦问题的特点以及高中学生现有的图形思维能力的分析，本文主要分析了以下几种解题策略：

策略1方程联消法，即联立两方程并加以相消的方法.首先将圆锥曲线方程与直线方程联立，再借助一元二次方程的相关特性，将二者相消的方法.

策略2两点作差法，即设点A(x1,y1)，B(x2,y2)为圆锥曲线与直线的交点，再将此二点代入圆锥曲线的方程式，加以作差，便可得出关于弦AB斜率及中点的方程式，用此种方法解题有助于提高解题效率.

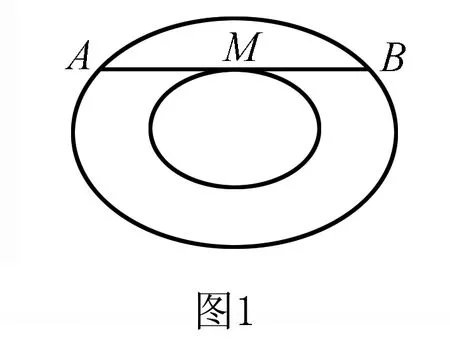
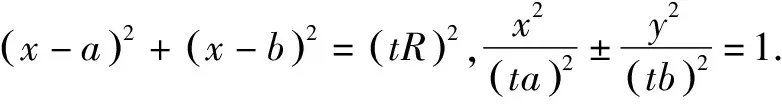
二、应用举例

类型1 弦中心为固定一点时，求弦的直线方程.

解析令椭圆与直线交点为A(x1,y1)，B(x2,y2).

所以直线方程为x+2y-4=0.

类型2已知弦所过定点的坐标，以及平行弦的中点坐标，解中点的轨迹方程

由题可见，弦的中点坐标涉及在内，而弦AB的斜率与MP的斜率相同，所以此题宜用两点作差解题策略.

解析令A(x1,y1)，B(x2,y2)，M(x,y),得

所以3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0.

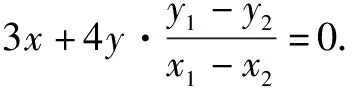
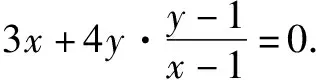
所以3x(x-1)+4y(y-1)=0.

又因为椭圆与直线l一定交于两点，点P又位于椭圆中，所以3x(x-1)+4y(y-1)=0即为点M的轨迹方程.

类型3 圆锥曲线上存在两点，并和其它直线对称的相关问题.

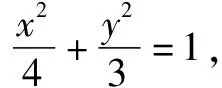
所以3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0.

所以弦P1P2的中点P的轨迹方程即为y=3x,它满足于直线y=4x+m必然相交于椭圆内这一条件.

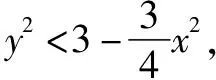
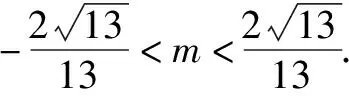
无一例外的是，在上述三种情况下，入住公办的养护院是照料者的一致首选。尤其是对于照料者去世后的情形，高达四成多的照料者选择入住公办的养护院。在最理想的情境下，入住公办的养护院也依然最受照料者的青睐。值得一提的是，在第三种情况下，照料者表露出对心智障碍成员社会融入的渴求——近三分之一的照料者希望这些成员能主要依靠助残日托照料(综合照料体系)来实现未来安置，而不是进入公办的养护院简单了事。在三种情形中，心智障碍成员由亲朋负责照料是入住公办的养护院与还没有计划后的主要选择。

类型4 圆锥曲线中的相关定值问题.

证明令A(x1y1),B(x2y2),且x1≠x2，得

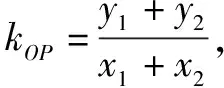
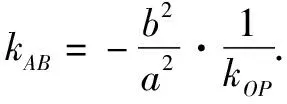
类型5参数值的范围问题.

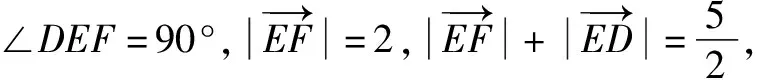
(1)求椭圆C的方程；

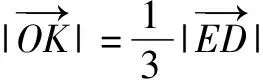
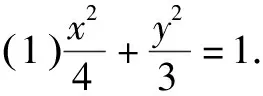
(2)设M(x1y1),N(x2y2)，H(x0，y0),直线l斜率为k(k≠0).

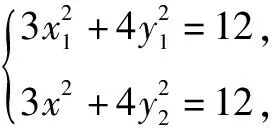
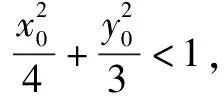
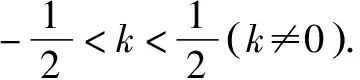
在有关圆锥曲线的点弦问题的教学中，除了上述几种解题策略外，还有许多可用的技巧.高中数学老师在加以运用的过程中要善于对其巧妙加工、综合运用，以加强学生对圆锥曲线相关问题的掌握程度.