数形结合在小学数学计算教学中的应用
刘福英

【摘要】数学基本思想是《义务教育数学课程标准(2011年版)》提出的“四基”之一,数形结合是数学思想中重要的思想方法。它可以把抽象的知识具体化,让数学知识的呈现更符合学生的年龄特征。在小学计算教学中利用数形结合的思想方法,可以让运算的意义、算理、算法更直观、更形象。
【关键词】计算教学;数形结合;以形解数;以形说理;以形助数
《义务教育数学课程标准(2011年版)》提出了“四基”的学习目标,数学基本思想也是其中一项。在小学数学教学中比较常见的数学思想有:数形结合思想、转化思想、统计思想和模型思想等。其中,数形结合既是一种数学思想,也是一种解决问题的方法,在小学数学教学中的应用比较广泛,尤其对于教师在计算教学中遇到的“部分学生对运算意义理解不深、对算理似懂非懂,面对同一类题型,时而会算,时而不会算”等情况,提供了一个很好的解决问题的办法。下面笔者就如何在小学数学计算教学中渗透数形结合思想谈谈个人的做法。
一、以形解数,促进学生对乘法分配律意义的理解
“以形解数”,是指通过直观具体的图形来解析情境中“数”的意义,是一种让知识更贴合学生的认知水平,同时又更有利于促进学生对知识的理解的教学方法。在小学数学计算教学中,运算律的运用贯穿于整个小学阶段始终,为整数、小数、分数的运算带来了极大的方便。小学阶段中的运算律主要有加法交换律及结合律、乘法交换律、结合律及分配律。而在这些运算律当中,学生最难掌握的则是乘法分配律,究其原因主要有两个:一是乘法分配律比较抽象,教师在教学这部分内容时,只是简单地把它当成计算课来教,没有让学生深入理解乘法分配律的意义,致使学生对乘法分配律的理解只是停留在运算方法的模仿上,而不知它的由来;二是乘法分配律的题型变化比较复杂,应用极其广泛,学生不能灵活运用。鉴于此,教师在教学这部分内容时,应当基于学生已有的知识水平,通过数形结合的方式,把抽象的运算意义具体化,让学生深入理解乘法分配律的意义,切实掌握乘法分配律。
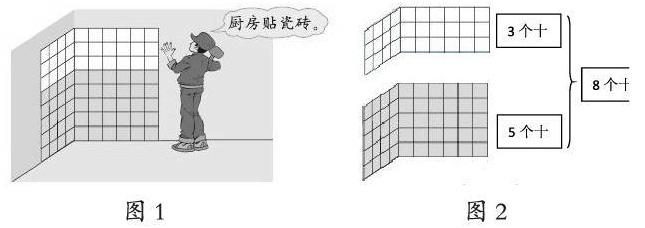
例如,北师大版四年级上册第四单元《运算律》中,对于乘法分配律这部分内容,教材是这样编排的(如图1):通过用不同的计算方法计算厨房里贴了多少块瓷砖,让学生感受3×10+5×10=(3+5)×10,4×8+6×8=(4+6)×8。在该课的教学中,教师应借助教材上的主题图来引导学生分别理解等式两边算式的意义,如:3×10+5×10是从颜色上观察,3×10表示3个10,也就是白色瓷砖的数量;5×10意为5个10,表示蓝色瓷砖的数量;白色瓷砖的数量和蓝色瓷砖的数量合起来就是8个十(如图2)。接着,教师可引导学生继续理解:(3+5)×10表示3行白色与5行蓝色合起来是8行,因为每行是10块瓷砖,所以白色瓷砖和蓝色瓷砖的总量也是8个十。然后,教师再追问,为什么等式的左右两边会相等呢?在此,除了让学生从计算结果说明原因,更重要的是引导他们从意义上理解——因为等式的左右两边都表示8个十,所以是相等的。若从瓷砖的位置观察,4×8+6×8=(4+6)×8也是同理。
教学中,通过“以形解数”的方法,让学生深入地理解乘法分配律的意义,它不仅仅是表面上两个算式的得数相同,其本质是指两个算式之间的涵义相同。这样,在之后进行的变式练习,如:125×99,125×101,125×99+125,125×101-125等诸如此类的练习中,学生就能够从理解运算意义的角度来思考,灵活运用乘法分配律进行计算,从而避免了学生对运算律方法生搬硬套的情况。
二、以形说理,促进学生对运算算理的理解
“以形说理”是指借助图形阐明算理,即阐明运算的道理。算理是算法的基础,也是学生计算的依据。学生只有充分理解了算理,才能灵活运用算法,在计算时做到“知其然并知其所以然”。但运算算理对于以具体形象思维为主的小学生来说往往也是比较抽象的,其实这也是学生理解的难点所在。要解决这一矛盾,教师就必须根据学生的年龄特征,化抽象为具体,用生动形象的图形解释算理,引导学生在计算时理解每一步计算的缘由。
例如,在三年级上册学生第一次接触“笔算两位数乘一位数”时,教材以《蚂蚁做操》为例,抽象出数学问题12×4=?,这是学生第一次学习用竖式计算乘法,与之前学过的加减法竖式计算不同的是,乘法竖式计算并不是把相同数位的数相乘,而是要用一位数分别去乘另一个乘数的每一位,再把所得的积相加,这是学生计算认识上的一次飞跃。对于学生来说,要掌握竖式计算的方法,最重要的是要理解竖式乘法运算中每一步的具体含义,这也是本节课的难点。根据三年级学生的年龄特点,我们可以采用直观模型——“点子图”来帮助学生理解算理,如,根据乘数12的个位和十位,把点子图分成2行与10行(如下图中)。先算2×4得到8个点子(如下图左),再用4×10,得到40个点子(如下图左),然后把两部分的积合起来,从而得到12×4的积是48。这是“两位数乘一位数”的乘法竖式计算的算理。在此基础上,我们可再引导学生理解竖式的简写形式,即先用4乘2得到8个点子,表示8个一(如下图右),8应写在个位;再用4×10,得到40个点子(如下图右),表示4个十,4应该写在十位,从而得到12×4的积是48。
通过这种“以形说理”的方法,将点子图与竖式计算完美结合,学生就能充分理解两位数乘一位数的运算算理,即在用竖式计算乘法时,不能把相同数位的数相乘,而是要用一位数分别去乘另一个乘数的每一位。在教学过程中,教师也可以引导学生多用点子图来解释竖式的意义,以达到让每个学生真正理解乘法竖式的计算算理的目的。
三、以形助数,促进学生对算法的迁移
“以形助数”是指通过用图形表示数,帮助学生掌握计算方法的数学方法。在四则运算的计算方法方面,整数加法、减法、乘法的计算,都是先从个位算起,唯独除法的计算与众不同——它是从高位算起。小学阶段整数除法的學习分为三个阶段:第一阶段是表内除法的运算,第二阶段是除数是一位数的口算和笔算,第三阶段是三位数除以两位数的笔算。其中,第二阶段的学习至关重要,因为它的计算方法可让学生迁移至第三阶段的学习当中。北师大版教材把第二阶段的学习内容安排在三年级下册,教材设计了两个梯度的学习:一是被除数的首位刚好是除数的整数倍,二是被除数的首位不是除数的整数倍。对于被除数首位刚好整除的情况,学生的理解难度不大,难点在于被除数首位不是除数的整数倍时,十位上剩余的数该怎么去处理。因为这种情况比较抽象,学生理解起来还是有一定的难度,所以,教师在教学这部分内容时,应借助小棒进行直观操作,帮助学生经历探索计算方法的过程。
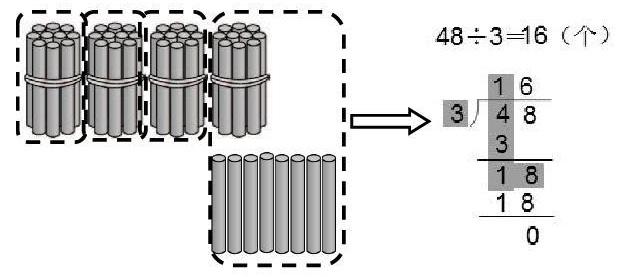
如,在教学《分橘子》一课时,教材利用48÷3=?来研究两位数除以一位数(首位有余数)的计算方法。教学时,教师可让学生用48根小棒代替48个橘子分一分。学生在分的过程中就会发现,这次分小棒与之前是不同的——十位和个位的小棒数,如果单独分的话都不能刚好分完,所以,在分小棒时要思考先分哪部分再分哪部分。学生按照以往的学习经验,可能会先分个位,再分十位,当发现这样分都会有剩余时,学生会把这两部分剩余的合起来再分。虽然这种分小棒的方法可以得到正确的得数,但是过程比较复杂。随后,教师可再引导学生探究更好的分小棒的方法——可以先分十位,把十位剩下的1捆与个位的小棒合起来再分,这种分小棒的方法只需两步就可以完成。在此基础上,教师再鼓励学生用竖式记录刚刚分小棒的过程(如下图),从而理解计算方法。
通过“以形助数”的方法,学生不仅能明白除法计算必须要先从高位算起的原因,而且能深入理解除法竖式计算每一步的意义,从而掌握计算方法,为学生的算法迁移奠定扎实的基础。
华罗庚在他撰写的《谈谈与蜂房结构有关数学问题》中提到“数与形,本是相倚依,焉能分作两边飞,数无形时少直觉,形少数时难少微,数形结合百般好,隔离分家万事休。”这段话深刻地揭示了“数”与“形”之间密不可分的关系。在小学数学计算教学中,我们通过把“数”与“形”相结合,将抽象的运算意义、算理及算法具体化、直观化,将逻辑思维与形象思维统一起来,让知识的呈现方式更符合学生的年龄特征和认知水平,这样学生就能获得问题解决的方法,从而进一步促进学生数学学习能力的提高。
参考文献:
[1]吴正宪,刘劲苓,刘克臣.小学数学教学基本概念解读[M].教育科学出版社,2014:50-54.
[2]付瑶.小学数学教学中渗透转化思想例谈[J].小学数学教育,2019(1-2):43-45.
责任编辑 罗良英

