非线性优化问题中的共轭梯度法研究综述

杨 雪，李 锋

(云南师范大学 数学学院，云南 昆明 650500)

优化问题与我们的工作和生活息息相关，比如每个公司都需要考虑“在一定成本下，如何使利润最大化或者损失最小化”的问题，此时，可以利用最优化方法去解决类似的实际优化问题．而优化问题存在有约束条件和无约束条件两种情况，也可将其称之为有约束优化和无约束优化．在处理实际问题时，通常会将有约束优化问题转变为无约束优化问题求解．因此，无约束优化一直是优化问题的研究重点．对于无约束优化问题，若目标函数连续可微，则可以利用最速下降法、牛顿法、拟牛顿法、共轭梯度法等方法对函数进行求解．这些方法都是利用目标函数的导数信息，然后采取一定的迭代格式求出目标函数的最优值[1]．

在上述方法中，最简单的方法是最速下降法，但其面对一些复杂的问题时会受到锯齿现象的影响导致收敛速度很慢．牛顿法和拟牛顿法的优势是收敛速度快，但由于其需要计算和储存矩阵且搜索方向的求解复杂，为大规模优化问题的求解增加了难度[2]．而共轭梯度法在计算时仅需求目标函数的一阶导数，且与最速下降法相比提高了收敛速度，同时又避免了牛顿法对存储空间的要求和求解Hesse矩阵及其逆矩阵的缺点．基于上述原因，在处理实际问题时共轭梯度法受到人们的广泛喜爱．

随着大数据时代的来临，亟须对海量数据进行分析应用，于是对大规模优化问题的求解提出新的要求．而具有收敛性强，且算法简单、易操作的共轭梯度法恰恰是大规模问题的重要求解方法之一[2]．因此，为了处理某些优化问题，研究共轭梯度法具有重要意义．

1 共轭梯度法的发展及其收敛性

1.1 共轭梯度法的发展

对于无约束优化问题：

min{f(x)|x∈Rn}，

(1)

1952年Hestenes等[3]提出了HS共轭梯度法，该方法不需要求逆矩阵或矩阵分解，而是以迭代的方式求线性方程的解，且结果具有有限终止性．对于一个线性方程组

Ax=b,x∈Rn,

(2)

其中，A是对称正定矩阵，且A∈Rm×n,b∈Rm．

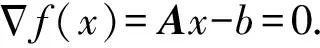
在解决了线性方程组的问题之后，如何将该方法推广到非线性领域值得关注．于是Fletcher等[4]将HS法的思想运用到非线性优化问题，并提出了FR法，FR法可先在精确线搜索下求解凸二次函数最小值问题，之后他们又将其推广到一般函数最小值的求解中[1]；1969年Polak等[5]和Polyak[6]提出了PRP方法，该方法通过对FR方法中βk的改动，改善了FR方法的收敛速度慢的情况；1987年Fletcher[7]在其著作中引入了CD法，即共轭下降法，从而得到了关于下降方向更好的性质；1991年Liu等[8]在PRP方法的基础上提出了LS法；1999年戴彧虹等[9]提出了在Wolfe线搜索条件下的DY方法；2001年戴彧虹等[10]提了DL法，该方法利用拟牛顿方程及HS方法的共轭性使得新算法在收敛性和下降方向上均有所改善；2004年Yabe等[11]根据DL方法的思想得到了YT方法．

不同的共轭梯度法区别在于βk不同，现将以上方法中的βk计算公式归纳如下：

(3)

(4)

(5)

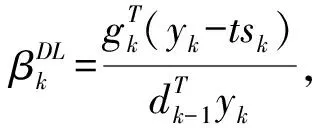
(6)

(7)

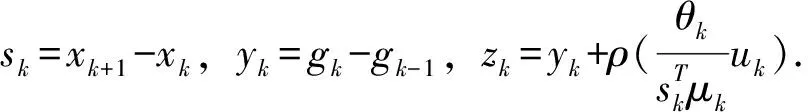
1.2 共轭梯度法的收敛性

1.2.1 FR方法

起初对FR方法的收敛性分析工作是在精确线搜索基础上展开，Zoutendijk[12]给出了精确线搜索下FR方法对一般非凸函数全局收敛的证明，之后，Powell[13]给出FR方法全局有效性，同时证明了精确线搜索下的FR方法若在某一步产生一个小步长则后面生成的步长也可能很小．因此，FR方法收敛可能很慢．此外，Powell[13]的分析也对FR方法数值表现不佳提供了一些依据．

由于精确线搜索计算量较大，实际计算通常采用非精确搜索确定迭代步长．1985年，Al-Baali[14]首先分析了FR方法在非精确搜索下的收敛性，且证明当参数满足0<ρ<σ<1/2;1/2时，FR方法在强Wolfe线搜索下满足充分下降性及全局收敛性；Liu等[15]继续研究了FR方法在强Wolfe线搜索下的收敛性，证明了当σ=1/2它也是充分下降且全局收敛的；1996年戴彧虹等[16]给出了FR方法在σ=1/2的强Wolfe线搜索时全局收敛的新证明，并还举出一个反例证明：当σ=1/2时FR方法可能因为产生上升方向而导致算法失败；此外戴彧虹等[17]还提出新的广义线搜索，并给出FR方法在广义线搜索下的全局收敛性；之后，戴彧虹等[18]在没有充分下降条件的情况下建立了FR方法和PRP方法的收敛性．

1.2.2 DY方法

由于前人对FR方法和CD方法的收敛性研究大多停留在精确线搜索或强Wolfe线搜索上，如何在较弱的线搜索条件下提出一种具有全局收敛性的共轭梯度法显得尤为重要．于是戴彧虹等[9]对原来的方法进行深入研究后，提出一种在Wolfe线搜索下能自动保持下降条件且全局收敛的共轭梯度法，并将其称之为DY方法．之后，戴彧虹[19]分析了DY方法的内在性质，给出了该方法在远离最优点时大部分迭代点列都满足充分下降条件的证明．

1.2.3 PRP方法

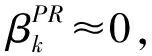
(8)

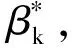
(9)

延续WYL方法的思想，2007年Yao等[24]将这种方法推广到HS和LS方法上，并提出新的算法，其形式如下：

(10)

(11)

(12)

2012年Dai等[26]受到文献[27]提出的新算法能够产生充分下降条件的启发下，对Zhang[25]的NPRP方法进行了改进，使改进后的NPRP方法在下降方向上具有更好的性能，并将该方法称为DPRP法．因此，DPRP方法和NPRP方法相比较，不仅对任意线搜索具有充分的下降性，而且在Wolfe线搜索或Armijo线搜索下非凸极小化都保持全局收敛性．此外，将这一结果推广到NHS方法，并称为DHS方法．其中：

(13)

(14)

2 共轭梯度法的研究现状及热点

目前，对于共轭梯度法的研究主要有两种思路：一种是直接改进共轭参数βk；另一种是利用混合方法能够取长补短的特点将不同的方法进行混合．众所周知，证明FR法、DY法和CD法的收敛性时，全局收敛定理只需要满足Lipschitz假设，而不需要有界性假设．这决定了它们虽然计算效果一般，却具有很好的全局收敛性．另外，由于PRP法、HS法和LS法能够自动调节βk避开干扰步长，具有内置重新启动功能，因此在一般情形下可能不收敛，但是它们却具有良好的数值表现．正是因为混合共轭梯度法具有结合两类方法优缺点的特点，所以从混合共轭梯度法的思路出发构造出一种既具有好的收敛性质，又具有优秀的数值表现的新算法具有深远的意义．

混合共轭梯度法一般是将其他共轭梯度法与经典共轭梯度法混合．1990年Touati-Ahmed等[28]首先通过将FR方法和PRP方法投影，引入了混合共轭梯度法．这是对混合共轭梯度法的一次有效尝试，新方法兼具FR方法和PRP方法的特点，并克服了FR方法数值表现一般的缺点，其中：

(15)

为扩展PRP更新参数的允许选择范围，同时保持全局收敛性，Gilbert等[22]提出：

(16)

该算法的数值表现虽然比FR方法好，但却不如PRP方法．由于DY方法具有比FR方法更好的全局收敛性，因此戴彧虹等[9]沿着这种思路给出一种混合DY方法和HS方法的新算法：

(17)

而且其以大量的数值实验证明该算法明显优于HS方法和DY方法，特别在面对较为复杂的问题时数值表现也比PRP方法好．由于受文献[22]的启发，何晓旭等[29]在2016年提出一种将FR和PRP算法混合的新算法．该算法充分利用二者的优势，下降方向dk由新算法产生且不依赖于任何一种线搜索条件．其中：

(18)

(19)

(20)

为了延续DPRP法[26]、DY法[9]等多种共轭梯度法的优点，韩信等[30]在2017年提出了一种新HZW法，其在发表的文章中不仅给出了新算法良好的收敛性证明，而且用文献[31]中的11个测试函数对它的数值表现进行了验证，其中：

(21)

除此之外，刘玲等[32]在2016年提出了一种新的带参数的共轭梯度法，并给出了新算法全局收敛性证明．新算法最大的特点是搜索方向满足充分下降性却不依赖任何线搜索，但引入参数的选取会对最后的数值效果造成一定的影响．其中βk为：

(22)

(23)

与此同时，利用两种方法的凸组合构造新算法的尝试也在进行．Andrei[33]给出了一种新的混合共轭梯度算法，其中：

(24)

对于这种方法，一个必须解决的问题就是凸组合参数θk确定．在文献[33]中，作者先假设搜索方向dk为牛顿方向，据此得出θk的表达式为：

(25)

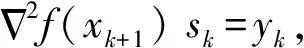
(26)

类似也可以得到dk的表达式，最终得到的dk在一定条件下为近似牛顿方向．但这种方法的局限性在于不能保证生成的dk一定是下降方法，因此可能导致数值结果不稳定．除此之外，作者还给出了新算法在一定条件下的收敛性证明以及数值实验表现．

Liu等[34]在Andrei[33]的启发下，综合考虑LS方法数值表现及DY方法的收敛性，提出了基于LS和DY方法凸组合的一种新的混合共轭梯度法，该方法下的搜索方向满足Dai等[10]提出的D-L共轭条件：

(27)

2019年Mtagulwa等[35]借鉴Alhawarat[36]和文献[34]的思想，构造了NPRP与FR方法的凸组合的新混合共轭梯度法．该方法继承了PRP、FR和NPRP共轭梯度的特点，并将βk更新为：

(28)

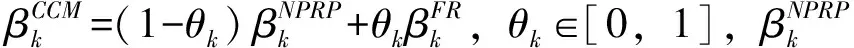
(29)

此外，关于凸组合的其他混合共轭梯度法还可以参见Djordjevic[37-38]提出的LS和CD方法凸组合的混合共轭梯度法及LS和FR方法凸组合的混合共轭梯度法．

目前，对混合共轭梯度法研究的方法已有很多，但对不同的混合方法而言，其优缺点、原理、算法特点以及收敛性特征等仍存在差异．因此对混合共轭梯度法进行深入研究仍具有重要意义，在未来研究中争取探索出更多兼具好的收敛性质及良好数值表现的混合共轭梯度法．

3 共轭梯度法的应用

由于共轭梯度法能够高效、简洁地处理一些大规模线性等式和非线性优化问题，在处理实际问题时，其应用范围广泛，如：图像复原、压缩感知问题和求解大规模非线性互补问题等．

3.1 共轭梯度法在图像复原中的应用

图像是获取信息的重要方式之一，为高效、快捷、精准地从图像中获取重要信息，对图像复原进行研究具有重要应用价值．图像复原的基本任务是最大限度地保留原始图像的边缘信息和去除污染图像中噪声及模糊部分．对污染图像的处理时，要先根据不同的污染情况建立相应的原始图像和污染图像的数学模型，然后利用污染图像信息，对建立好的数学模型进行反解[39]．因此图像复原本质上可以看成是数学中反问题的研究范畴．在得到一个数学模型后，可以先对最小化模型进行离散处理，然后再利用最优化方法对离散后的模型进行求解．而离散模型其中的一个子问题需要对大规模线性方程组进行求解，此时就可以利用共轭梯度法来实现．

2020年Yuan等[40]将最速下降算法和LS方法进行凸组合，提出了一种修正的共轭算法．新算法的搜索方向在没有任何线搜索技术的情况下，具有充分下降性和信赖域性质，在一定的条件及回溯线搜索技术下建立了全局收敛性[41]．此外，为了改善目标函数值会随迭代次数增加而缩减的情况，作者对步长采用了加速系统[42]，并将该算法成功的应用到图像复原中，而且数值实验表明，该算法与其他方法相比具有一定的优势．同年，Cao等[43]提出了一种修正PRP共轭梯度法，由新算法定义的搜索方向具有充分下降性和信赖域特征．由于这两个特别好的特性，因此能够更简单地证明非凸函数在Armijo线搜索下的全局收敛性．同时作者还用数值实验证明了在图像复原背景下新算法同PRP方法相比具有较大优越性．

3.2 共轭梯度法在压缩感知中的应用

2006年Donoho[44]和Candes等[45]的两篇突破性的论文使压缩感知进入了大众视野．随着现代科学技术的迅猛发展，压缩感知方法已经广泛应用在电子工程、医学、计算机科学等领域．它利用一个高度不完备的线性测量对稀疏信号进行采样，这时获取的是被“压缩”后的数据．然后，通过使用高效的方法对“压缩”的数据进行重构就能恢复原稀疏信号[46]．在进行第2步重构时，就可利用共轭梯度法恢复原始信号．

在处理信号恢复模型时，由于l1-范数是非光滑凸函数，给l1-范数最小化问题的求解带来了一定难度．李双安[47]利用Nesterov光滑技术把l1-范数近似为一个光滑函数，原问题就转变成求解光滑无约束凸规划问题，然后利用改进的HS算法求解该问题，从而达到大规模稀疏信号恢复的目的．

与前述类似，王慧敏等[48]为解决l0-范数非凸非连续无法用凸优化算法求解的问题，基于Gauss函数提出一个新的光滑函数逼近l0-范数．因此原模型就转化成可用凸优化算法求解的凸优化问题，作者在研究中选择PRP法完成了信号恢复过程．

4 小结

共轭梯度法是解决大规模线性等式和非线性优化问题的重要方法之一，其突出优点是收敛性强、迭代步骤简单、对存储要求低．本文分别介绍了几种经典共轭梯度法及其改进算法的发展变化和收敛性，然后描述了混合共轭梯度法的研究现状以及共轭梯度法在图像复原和压缩感知中的应用．

现有的共轭梯度法在实践中取得了优异的表现，但部分算法尚存在易受参数影响、适用于特定的函数、可能需要在特定条件下证明收敛性等局限性，因此凸组合法中凸组合参数的选取、对新共轭梯度法的优化以及在更弱的搜索条件下证明算法的收敛性等问题有待于后期进一步的研究和完善．除此之外，结合谱方法的谱共轭梯度法中谱参数的选择、三项混合共轭梯度法等也值得今后继续挖掘和拓展．