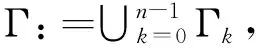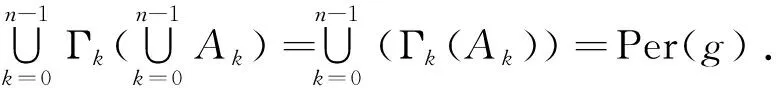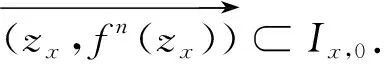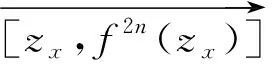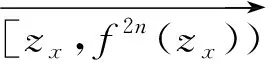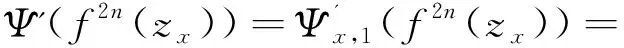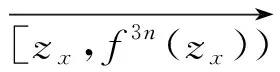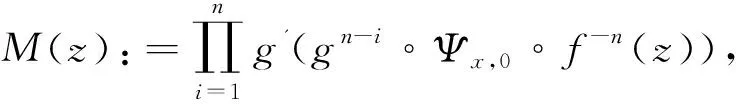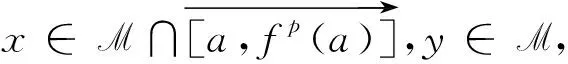带有周期点圆周自同胚的光滑共轭问题
楚 鹏
(重庆师范大学 数学科学学院, 重庆 401331)
0 引言
在动力系统理论中,共轭方程是指
φ∘f=g∘φ,
(1)
此外,当f和g是圆周S1上的保向Cr微分同胚时,对方程(1)的研究同样也吸引了若干著名学者的注意.早在19世纪末,Poincaré发现当r=0时(这时f是一个保向自同胚),如果f的旋转数是有理数,则f有相对简单的动力学行为.然而,旋转数是无理数的情形则未知.直到1932年,Denjoy[7]通过研究f与刚性无理旋转之间的共轭关系,才完全了解无理旋转情形下f的动力学行为.实际上,Denjoy定理告诉我们对于f∈C2和无理数ρ存在一个保向自同胚解φ,使得满足共轭方程φ∘f=τρ∘φ,其中τρ=z+ρ是圆周上旋转角度为ρ的刚性旋转.进一步,Arnold[8]首次考虑了φ的光滑性,得到了一个局部结果,即在τρ足够接近光滑微分同胚f时共轭方程(1)成立.后来,Herman[9]得到了一个全局的光滑结果.
另一个方面,当f和g的光滑度低于C2时,1999年,K.Ciepliński[12]对于圆周上连续系统ft和gt给出了共轭方程φ∘ft=gt∘φ成立的充要条件,并且给出了此方程保向同胚解的一般形式.2002年,K.Ciepliński等[13]对于圆周上无周期点的离散系统f和g,证明了方程(1)存在唯一的连续解,且在整个圆周都是f的极限集时该解是一个同胚映射.2007年,M.C.Zdun[14]研究了圆周上具有周期点的保向(或逆向)自同胚,得到了方程(1)保向(或逆向)同胚解存在的充要条件,并给出了其一般构造方法.本文在文献[14]的基础上进一步考虑在圆周上具有周期点的保向Cr(r≥1)微分自同胚的f和g之间的共轭问题.
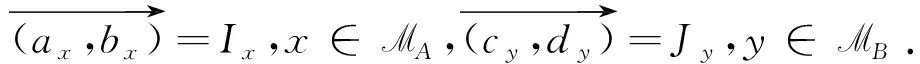
定义2设一个映射ξf:M→{1,-1},∀z∈Ix⊂M,
(2)
接下来我们利用数论中一个非常重要的定理来定义共轭数与特征数.
定义3[14]若q,n∈N+,gcd(q,n)=1,1≤q 下面是本文主要结果: 定理1设f,g:=S1→S1是周期n≥1的保向自同胚,ρ(f)=ρ(g),且存在a∈Per(f),b∈Per(g)和一个保向的双射 使得 ξf(x)=ξg(gen Γ0(x)), (3) 其中ρ(f),ρ(g)分别为f,g的旋转数,p=charf. (i)若f和g是保向C1微分同胚,F,G分别f,g的任意一个提升,且满足 0 (4) 0 (5) (ii)进一步,若f和g还是Cr(r>1)的,且对任意非周期点zx∈S1在初始区间[zx,fn(zx)]端点处满足条件 (6) 其中 下面我们主要给出一些符号的说明,同时为了方便在第2、3节定理1两部分结论的证明,在本节会提及几个重要的引理. 我们把圆周S1视为单位模复数的集合,对于任意的u,w,z∈S1,存在唯一的t1,t2∈[0,1),使得we2πit2=u.于是我们可以定义圆周上的一种序关系,即uwz当且仅当0 对于任意两个给定的Cr微分同胚f,g:S1→S1,如果存在一个Cr微分同胚φ满足共轭方程(1),我们称f与g是Cr共轭.若这里φ是保向(逆向)Cr微分同胚,则f与g称为保向(逆向)Cr共轭.若对于保向的Cr微分同胚f:S1→S1,存在一个严格递增的Cr映射F:R→R,使得 f(e2πix)=e2πiF(x),x∈R. 其中F满足F(x+1)-F(x)=1,x∈R,那么F称为f的一个提升. 对任意给定的保向Cr微分同胚f,F是其任一提升,我们把 Per(f,n):={z∈S1:fn(z)=z,fk(z)≠z,1≤k 接下来我们将讨论具有周期点的同胚映射的若干性质,即引入周期点之间的对应关系.从现在开始,若f未进行具体说明,都指的是保向的且旋转数为有理数同胚映射. 引理2对于给定的保向Cr微分同胚f和g,若方程(1)存在一个保向Cr微分同胚解φ,则ρ(f)=ρ(g)(mod 1),charf=charg. 引理3[14]若Per(f,n)≠∅,n≥2,p=charf,则对于每个a∈Per(f),有 满足fip(zk)=zk+i(mod n),k=1,…,n-1,其中{z0,z1,…,zn-1}是引理1中定义的. 假设S1≠Per(f)≠∅,由于Per(f)是S1的闭子集,则Κ(f)可表示为S1Per(f)上至多可数个互不相交的开弧的并集,故类似引理1和引理3可定义圆周S1上各互不相交开弧之间的关系. 则有: f(Ix,k)=Ix,k+q(mod n), (7) fip(Ix,k)=Ix,k+i(mod n), 其中Ix,k,x∈M,k=0,…,n-1,记Ix,0=Ix. 其中MA,MB分别是圆周S1上闭子集A,B的各余区间中点的集合,Ix,x∈MA是互不相交的开弧Jy,y∈MB也是互不相交的开弧. 引理5[14]设A=Per(f),B=Per(g),Γ:A→B是一个保向的双射,则存在一个唯一的保向的双射h:MA→MB使得 (8) 定理1(i)的证明 由假设可知f,g是S1上保向C1微分同胚,则其对应提升F,G是R上周期为1的严格递增的连续可微函数,故对∀x,y∈[x0,Fp(x0)], 则有 |F(y)-F(x)|≤F′(ξ)|x-y|≤ (9) 同理对于∀x,y∈[y0,gp(y0)],有 |G(x)-G(y)|≤LG|x-y|, (10) 这里 由(4)式,存在足够小的正数δ1,δ2,使得 0 (11) F′(x)>1,∀x∈[x0,x0+δ2]. (12) 同理由(5)式有 0 (13) G'(y)>1,∀y∈[y0,y0+δ2]. (14) 对于∀zx∈Ix,0,有fn(zx)∈Ix,0.定义初始区间的保向C1微分同胚 |φx,0(x)-φx,0(y)|≤Lφx,0|x-y|α. (15) 又对于∀zx∈Ix,0,有fkn(zx)∈Ix,0,k∈Z,因此通过正向迭代的共轭方程, (16) 可定义保向C1微分同胚 同理通过负向迭代的共轭方程 (17) 可定义保向C1微分同胚 令 Ψ(z):= 则 Ψ(f(z))=g(k+1)n∘Ψx,0∘f-(k+1)n(f(z))= g∘gkn∘Ψx,0∘f-kn(z)=g(Ψ(z)), 并且在连接点处连续是显然的,这样我们就得到了Ψx,k(z)是方程(1)的连续解.可类似验证Ψx,-k(z)也是方程(1)的连续解.由Ψ(z)的构造易见它是一个双射,再结合引理6可知对于每个保向的双射都是同胚的,故我们得到了Ψ(z)是满足共轭方程(1)的保向同胚解. 则有 (18) (19) 同理对于 (20) 记上述区间上的序列φx,k=φ.当k∈[-M,M]时,即对于 有 其中 令LG(LF-α)=b0∈(0,1),有 |φ(y*)-φ(x*)|≤L1|y*-x*|α. 综上所述, |φ(x)-φ(y)|≤L|x-y|α, ∀x,y∈[x0,FP(x0)]. 其中L:=max{L0,L1,L2}. 在这部分我们主要考虑有理旋转的保向Cr微分同胚f,g之间的共轭关系,即验证在非周期点集上存在一个保向Cr微分同胚解φ:=S1Per(f)→S1Per(g),使得对于给定的f,g是保向Cr共轭的,并在定理的证明中给出了Cr微分同胚解φ的一般性构造. 定理1(ii)的证明 首先考虑将Γ0延拓到周期点集上,即验证方程(1)存在唯一的保向同胚解Γ:Per(f)→Per(g),延拓之后的保向同胚解可将圆周拆分成n个部分,如此以方便对非周期点集上解存在性的进行逐段讨论. 当Per(f)=Per(f,1)时,即f的周期n=1,那么根据定义3可知charf:=0,那么p=0,因此 即有Γ0=Γ,显然满足方程(1). 当Per(f)=Per(f,n),n≥2时,ρ(f)=ρ(g),令 k=0,…,n-1. Γk(z):=gk-n∘Γ0∘fn-k(z),z∈Ak,k=0,…,n-1, (21) 又对于每一个Γk是保向的,所以Γ也是保向的,由引理6可见,Γ是保向同胚的,下面我们来证明Γ满足方程(1). 设∀z∈Ak,则f(z)∈f[Ak]=Ak+1,这里0≤k Γ(f(z))=Γk+1(f(z))=gk+1-n∘Γ0∘fn-k-1(f(z))=gk+1-n∘Γ0∘fn-k(z)=g∘gk-n∘Γ0∘fn-k(z)=g∘Γk(z)=gΓ(z), 当k=n-1,则f(z)∈f[An-1]=A0,再次利用(21)式,则有 g(Γ(z))=g(Γn-1(z))=g∘gn-1-nΓ0∘fn-(n-1)(z)= Γ0(f(z))=Γ(f(z)), 因此存在满足上述条件的Γ使得Γ∘f=g∘Γ成立.唯一性的证明是显然的,故我们有唯一的保向同胚Γ:Per(f)→Per(g)满足方程(1). Ψx,0(fn(zx))=gn(Ψx,0(zx)). (gn∘Ψx,0∘f-n)'(f2n(zx))=g'(gn-1∘Ψx,0∘f-n(f2n(zx)))g'(gn-2∘Ψx,0∘ (f-n(f2n(zx)))(f-n)'(f2n(zx))=g'(gn-1(Ψx,0(f2n(zx))))g'(gn-2(Ψx,0 (f2n(zx))(f-n)'(f2n(zx)). (gn∘H∘f-n)'(f2n(zx))=g'(gn-1(H(fn(zx))))g'(gn-2(H(fn(zx))))…g'(H(fn(zx)))H'(fn(zx))(f-n)'(f2n(zx))=g'(gn-1(Ψ(fn(zx))))g'(gn-2(Ψ(fn(zx))))…g'(Ψ(fn(zx)))Ψ'(fn(zx))(f-n)'(f2n(zx))=g'(gn-1(Ψx,0(fn(zx))))g'(gn-2(Ψx,0(fn(zx))))…g'(Ψx,0(fn(zx)))Ψx,0'(fn(zx))(f-n)'(f2n(zx)), (22) (23) 由(22)式,利用Newton-Leibniz公式归纳得到在连接点f2n(zx)处 同理由(23)式可得到 接下来我们考虑φx,k在所有非周期点集上都是Cr的,其中特别地φx,k|Ix,0=Ψ.当Per(f)=Per(f,1)时,φx,0就是我们要找的,由上面讨论显然成立. 当Per(f)=Per(f,n),n≥2时,设共轭方程 φx,k(z):=gk-n∘φx,0∘fn-k(z),z∈Ix,kq(mod n),k=0,…,n-1. (24) 由(7)式可知 fn-k(Ix,kq(mod n))=fn-k-1f(Ix,kq(mod n))=fn-k-1(Ix,kq+q(mod n))=fn-k-2f(Ix,kq+q(mod n))=fn-k-2(Ix,((kq+q)(mod n)+q)(mod n)) =fn-k-2(Ix,kq+2q(mod n))=…=Ix,kq+(n-k)q(mod n)=Ix,0. (25) 同理有 gn-k(Jh(x),kq(mod n))=Jh(x),kq+(n-k)q(mod n). 由(24)和(25)式有 φx,k(Ix,kq(mod n))=gk-n∘φx,0∘fn-k(Ix,kq(mod n))=gk-n∘φx,0(Ix,kq+(n-k)q(mod n))=gk-n∘φx,0(Ix,0)=gk-n(Jh(x),0)=Jh(x),0+(k-n)q(mod n)=Jh(x),kq(mod n), 故通过上述共轭方程可定义映射φx,k:Ix,kq(mod n)→Jh(x),kq(mod n),k=0,…,n-1.因为每一个φx,k是关于φx,0的共轭方程,所以φx,k是保向Cr微分同胚.记φx,k=φ|Ix,kq(mod n),接下来我们验证对于每一个φx,k满足(1)式. f(Ix,kq(mod n))=Ix,(k+1)q(mod n), 所以,当0≤k φ(f(z))=φk+1f(z)=gk+1-n∘φx,0∘fn-k-1(f(z))= g∘gk-n∘φx,0∘fn-k(z)=g∘φx,k(z)=g(φ(z)). 当k=n-1时, g(φ(z))=g(φn-1(z))=g∘gn-(n-1)∘φx,0∘fn-(n-1)(z)= φx,0∘f(z)=φ(f(z)). 最后验证 (26) 设y∈M,存在k∈{1,…,n-1},使得 (27) 同时,对于Iy必定存在x∈M,使得f(n-k)p(Iy)=Ix,结合(27)式,则有 其中fnp(a)=a,a∈Per(f).由定义3,有 f(k-n)p(Ix)=Ix,(k-n)pq(mod n)=Ix,kpq(mod n)=Ix,k(mod n) 又因为存在映射χ:=k→kq(modn),使得映射χ是双射,因此我们就得到了 同理可证(26)式. 综上所述,我们得到了在非周期点集上存在一个保向的Cr微分同胚解φ:S1Per(f)→S1Per(g)满足(1)式.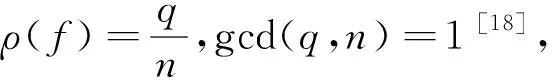
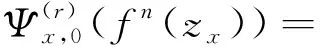
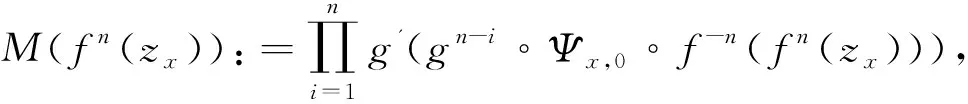
1 预备知识
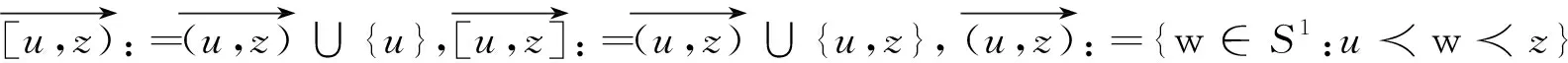

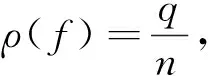

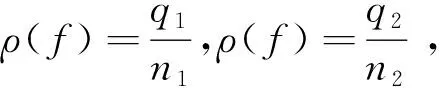
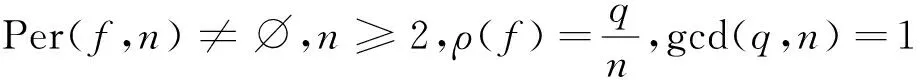
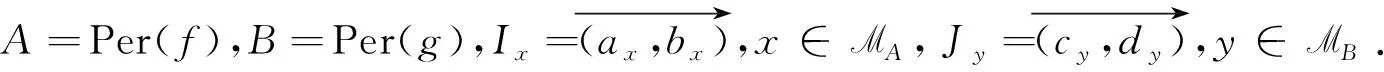
2 共轭映射的全局连续性

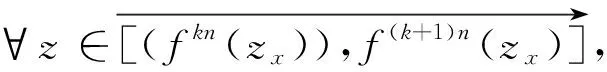

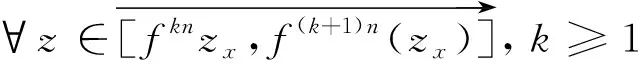
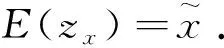
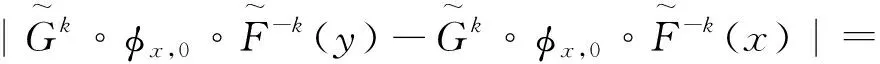
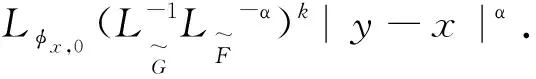
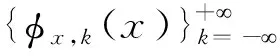
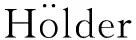
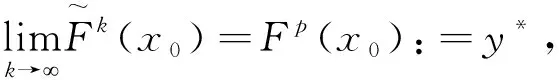
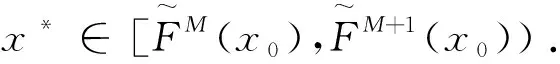



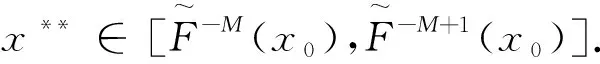

3 共轭映射的局部Cr光滑性