具强阻尼的Sine-Gordon型吊桥方程的长时间动力学行为研究

吕鹏辉，吕小俊

(苏州大学 应用技术学院，江苏 苏州 215325)

本文所研究的具强阻尼的Sine-Gordon型吊桥方程的长时间动力学行为：

utt-Δut+Δ2u+k2u++g(sinu)+f(u)=h(x)，(x，t)∈Ω×[0， ∞)，

(1)

u(x， 0)=u0(x),ut(x， 0)=u1(x)，x∈Ω，

(2)

u(x，t)=Δu(x，t)=0，x∈Γ.

(3)

其中Ω是R中具有光滑边界的有界域， 其光滑边界为Γ，k2是弹性系数， 函数为：

1990年吊桥方程由A.C.Lazer和P.J.Mckenna[1]作为非线性分析领域的新问题提出， 该方程描述了吊桥路面在垂直平面内的震动． 吊桥方程提出来之后， 众多学者对该模型进行了许多相关研究． 其中：Park等[2]得到了非线性阻尼吊桥方程的整体吸引子的存在性； 刘世芳等[3]研究了带有历史记忆的阻尼吊桥方程的长时间行为， 并通过利用收缩函数的方法， 获得解在强拓扑空间下全局吸引子的存在性． 随着对该方程地研究深入， 许多学者对各类吊桥方程的长时间性态进行了研究， 如自治吊桥方程的整体吸引子[4-5]， 维数估计[6-7]， 吊桥方程的指数吸引子[8-9]， 非自治吊桥方程的拉回吸引子[10-11]等. Sine-Gordon方程是波动方程中的一个重要模型， 具有丰富的物理背景， 对该类方程的长时间行为(包括整体吸引子、 指数吸引子、 维数估计等)也有许多学者进行了研究， 可参见文献[12—16]及其他相关文献． 张建文等[12]利用算子半群理论证明了在一定边界条件下系统存在连续解， 并且由算子半群分解的方法构造出渐近紧的不变吸收集， 进而得到系统整体吸引子的存在性．

有许多学者[17-19]研究了Kirchhoff型吊桥方程的长时间动力学行为． 而有关Sine-Gordon型吊桥方程的研究相对甚少． 因此， 本文在前人研究的基础上， 根据吊桥方程和Sine-Gordon方程的特点， 研究具强阻尼Sine-Gordon型吊桥方程吊桥的长时间动力学行为， 包括在空间X=G2×H的整体吸引子的存在性， 整体吸引子A的Hausdorff维数及分形维数有限.

1 预备知识及相关理论

G4⊂G2⊂H⊂G-2，

其中G-2为G2的共轭空间．

下面定义Hilbert空间， 并赋予范数：

下文中出现的λ1为-Δ的第1特征值，Ci为不同正常数，Ci(·， ·)为依赖括号内的不同正常数． 为得到问题(1)～(3)的长时间动力学行为， 接下来给出相关理论．

引理1[20-21]若在Banach空间X中定义的一个连续半群{S(t)}t≥0满足下列条件：

1)存在一个有界吸收集B⊂X， 使得对任意有界集B0⊂X， dist(S(t)B0，B)→0(t→+∞)；

2)S(t)可分解为S(t)=P(t)+U(t)， 其中P(t)是X→X的一个连续映射， 且对每个有界集B0⊂X， 使得：

则连续半群{S(t)}t≥0存在整体吸引子．

引理2[20]设半群S(t)在整体吸引子A上是Frechet可微的， 且存在时间t0， 使得对所有的t>t0是紧的， 若qm<0， 则整体吸引子A的Hausdorff维数和分形维数是有限的， 其中，

2 整体吸引子的存在性

定理1假定(H1):f∈C′(R)， 且

(4)

(5)

(6)

问题(1)～(3)存在唯一整体解u∈L∞(0， +∞；G2)，ut∈L∞(0， +∞；H).

注：由假设(H1)(4)可知， 存在两个正常数C1，C2及η>0， 使得：

f(s)s+ηs2+C1≥0，F(s)+ηs2+C2≥0．

(7)

证明方程(1)与ut作H内积得到：

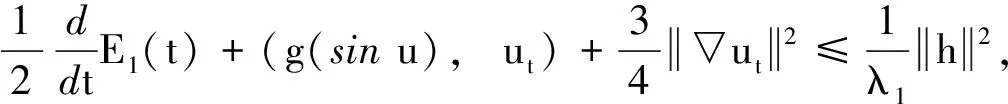
(8)

(9)

结合(8)式和(9)式， 得：

(10)

由Gronwall不等式， 得：

(11)

令v=ut+εu， 则方程(1)可写为：

vt-εv+ε2u-Δv+εΔu+Δ2u+k2u++g(sinu)+f(u)=h(x)，

(12)

方程(12)与v作H内积得到：

(13)

(14)

由假设条件得：

(15)

(16)

将(15)～(16)式代入(13)式得：

(17)

(18)

(19)

(20)

所以， 对∀R1>0， 存在t1， 使得：

由此， 可以得到G2×H的有界吸收集．

则B1是在G2×H中的有界吸收集．

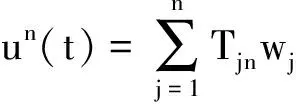
(21)

其中j=1， 2， …，n， 当n→∞时， 在G2×H中， (u0n，u1n)→(u0，u1).

对(21)在(0，t)上积分， 则有：

(22)

|g(sinun)-g(sinu)|≤3c1|un-u|，

即有：

两边对t求导， 再由wj在G2中的稠密性知：

utt-Δut+Δ2u+k2u++g(sinu)+f(u)=h(x)，

即u∈L∞(0，T；G2)，ut∈L∞(0，T；H)∩u∈L2(0，T；G1).

接下来， 证明解的唯一性.

令u(t)，v(t)是方程(1)～(3)对应于初值(u0，u1)， (v0，v1)的两个解， 则w(t)=u(t)-v(t)满足：

wtt-Δwt+Δ2w+g(sinu)-g(sinv)+f(u)-f(v)+k2(u+-v+)=0，

(23)

(23)式与wt作H内积得：

=(k2(v+-u+)+g(sinv)-g(sinu)+f(v)-f(u)，wt).

(24)

根据假设条件、 Holder不等式、 Young不等式和Poincare不等式， 得：

(25)

(26)

(27)

将(25)～(27)式代入(24)式， 得：

(28)

运用Gronwall不等式可得解的唯一性,则解的唯一性证明完毕． 此外， 由定理1， 则B1是半群{S(t)}t≥0在X中的有界吸收集， 从而有下列定理．

定理2在定理1假设条件下， 则球B1=BX(0，R1)是问题(1)～(3)生成的解半群{S(t)}t≥0在X中的有界吸收集， 即对X中任意有界集B， 存在t1=t1(B)， 使得当t≥t1(B)时， 有S(t)B⊂B1.

接下来， 为得到整体吸引子， 将解半群进行分解， 具体如下：

设u=v+z， 其中：

ztt-Δzt+Δ2z=0，z(0)=u0，zt(0)=u1;

(29)

vtt-Δvt+Δ2v=h-f(u)-g(sinu)-k2u+:=φ，v(0)=0，vt(0)=0．

(30)

引理3如果 (u0，u1)∈B， (z，zt)是(29)式的解， 则

且

R(t)→0， 当t→+∞.

证明(29)式分别与zt，εz作H-内积， 得：

(31)

由定理1假设条件， 则存在正常数κ，ρ， 使得：

(32)

(33)

(34)

(35)

通过Gronwall不等式得到：

(36)

引理3结论证明完毕．

引理4如果(u0，u1)∈B， (v，vt)为(30)式的解， 则存在紧集N(T)⊂X且(v，vt)∈N(T).

证明对(30)式两边同时乘以算子A1/4， 得到：

ξtt-Δξt+Δ2ξ=A1/4φ，ξ(0)=0，ξt(0)=0，

(37)

其中ξ=A1/4v． 令η=ξt+εξ， 则

ηt-εη+ε2ξ-Δη+εΔξ+Δ2ξ=A1/4φ，

(38)

(38)式中的方程与η作H-内积， 得到：

(39)

由定理1假设条件， 得：

(40)

(41)

(42)

结合(40)～(42)式， 得：

(43)

(44)

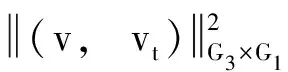
(45)

根据G3×G1→X是紧嵌入的， 则得到G3×G1的有界集是X的紧集． 引理4结论证明完毕．

定理3在定理1的假设条件下， 由问题(1)～(3)生成的连续解半群{S(t)}t≥0在X中存在紧的整体吸引子．

证明定义P(t)(u0，u1)=(z(t)，zt(t))，U(t)(u0，u1)=(v(t)，vt(t)).

显然，S(t)=P(t)+U(t)． 引理3表明任意的(u0，u1)∈B⊂X， 算子P(t):X→X是连续的， 并且满足引理1的2)． 同时， 引理4表明U(t)是一致紧的． 再由定理2， 存在有界吸收集， 所以{S(t)}t≥0在X中具有紧的整体吸引子． 定理3证毕．

3 整体吸引子的维数估计

定理4在定理1假设条件下， 问题(1)～(3)生成的整体吸引子A的Hausdorff维数、 分形维数有限．

证明问题(1)～(3)形式上的线性化方程为：

Utt-ΔUt+Δ2U+k2Ut+g′(sinu)cosu·U+f′(u)U=0，U(0)=ξ，Ut(0)=ζ．

(46)

第1步证明变分方程解的存在性， 方法类似于证明整体解的存在性， 并结合定理1可知存在唯一解U， 且(U，Ut)∈L∞(R+，G2×H)．

第2步证明S(t)在A上是一致可微的．

定义L(t，φ0):G2×H→G2×H，L(t，φ0)(ξ，ζ)=(U，Ut)，φ0∈A， 则

L(t，φ0)=DS(t)φ0，

证明S(t)在X=G2×H上的有界集上是Lipschitz连续．

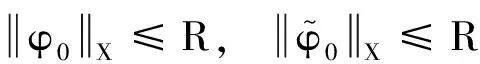
φ(0)=ξ，φt(0)=ζ，

(47)

在(47)两端用φt作H内积， 得：

(48)

(49)

(50)

(51)

将(49)～(51)式代入(48)式， 则有：

(52)

由Gronwall不等式， 得到：

即

令ϑ=φ-U， 则ϑ满足：

ϑtt-Δϑt+Δ2ϑ+g′(sinu)cosu·ϑ+f′(u)ϑ=F，

(53)

对(53)两端用ϑt作H内积， 则有：

(54)

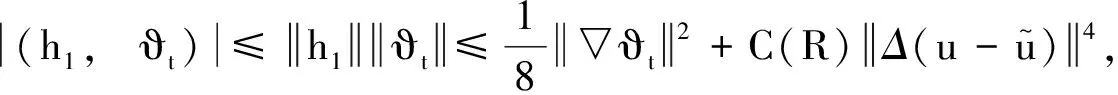
(55)

(56)

(57)

将(55)～(57)式代入(54)式， 则有：

(58)

由Gronwall不等式知：

所以， 对任一t， 当(ξ，ζ)→0时， 有：

即得到S(t)在A上是Frechet可微的.

第3步整体吸引子A的Hausdorff维数、 分形维数有限．

首先把方程(1)～(3)写成在空间X上的一阶抽象发展方程.令ψ=(u，ut+εu)T， 则ψ满足

ψt+Λεψ+G(ψ)=0，ψ(0)=(u0，u1+εu0)T，

(59)

其中

G(ψ)=(0，h(x)-k2u+-g(sinu)-f(u))T，

其中I为恒等算子．

记{Sε(t)}为由(59)式生成的群， 则对φ0=(u0，u1)T∈X，Sε(t)φ0=RεS(t)R-εφ0， 其中Rε是X中的一个同构Rε:(u，ut)→(u，ut+εu)．

所以， 记A为{S(t)}的整体吸引子， 则RεA为{Sε(t)}的整体吸引子， 且它们有相同的维数.现估计RεA的维数． 而(59)式的一阶变分方程为：

Ψt=-ΛεΨ-G′(ψ)Ψ≡F′(ψ)Ψ，

(60)

其中，Ψ=(U，Ut+εU)T，G′(ψ)Ψ=(0， -k2U+-g′(sinu)cosu·U-f′(u)U)T， 初始条件为：

Ψ(0)=ω=(ξ，ξt+εξ)T∈X.

(61)

设Ψ1(τ)，Ψ2(τ)， …，Ψm(τ)为(60)～(61)式分别对应于初值ω1(τ)，ω2(τ)， …，ωm(τ)，ωi∈X的解， 并记Φj(τ)=(ξj，ζj)T，j=1， 2， …，m为空间Qm(τ)E0=span{Φ1(τ)，Φ2(τ)， …，Φm(τ)}的一组标准正交基， 则：

根据引理3， 存在M>0，α≥0， 使得：

(62)

根据引理4， 存在常数c>0， 使得：

U(t，φ)G2+δ×Gδ≤c， ∀φ∈A，t≥0， 0<δ<<1，

(63)

(64)

因此， 根据(62)～(64)式， 得到：

综合上述， 得到：

其中λj，j=1， 2， …，m为-Δ的前个特征值， 所以

(65)

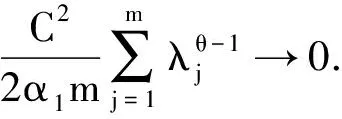
qm<0.

(66)

根据文献[22]可得，RεA的Hausdorff维数(dimH)和分形维数(dimf)分别满足：

dimH(RεA)≤m， dimf(RεA)≤2m，

这里的m由(66)决定， 所以

dimH(A)≤m， dimf(A)≤2m，

证毕.