整流板对T型分流三通管局部阻力特性影响的数值研究

李 优，叶学民，周 飞，李春曦

（华北电力大学电站设备状态监测与控制教育部重点实验室，河北 保定 071003）

在复杂的管网系统中，三通管作为分流的主要部件，广泛应用于各个领域。流体经过三通管后，在三通管下游形成漩涡，会出现流体总压和能量的损失，三通管的局部阻力对管道的流量分配及管路系统的经济运行有着显著影响。因此，开展三通管道的阻力特性及结构优化研究，对流体分配平衡及安全经济输送具有实际参考价值。

近年来，数值计算技术以其计算速度快、灵活性强、结果可靠等优点，越来越广泛地应用于管道设计与优化。目前，关于三通管的阻力特性已开展了许多有意义的探索。Costa等人[1]对圆角和尖角90°三通管进行实验研究，得出分支管局部阻力大于主管，圆角三通分支管回流区较小，从而降低了其局部阻力。Benes等人[2]用EARSM模型模拟了方形和圆形三通管结构，得到其内部压力分布。陈江林等[3]对T型三通管水力特性进行数值模拟与实验研究，指出垂直支管能量损失约为水平支管的3.25倍，水平支管能量损失随管径比增大而减小。石喜等[4]对2种PVC三通管进行研究，得到三通管局部阻力系数随雷诺数的变化。Kou等人[5]指出树状管网的局部阻力随支管长度比、支管数量的增大而减小。巩启涛等[6]采用数值计算方法模拟了大直径三通管的局部阻力系数随管径比、管间夹角的变化。

为降低三通管的阻力特性，多位学者开展了结构优化研究。Li等人[7]运用实验与模拟相结合的方法，指出在三通及弯头回流区安装适当高度的楔形部件可减小局部阻力。Gao等人[8]在管道分流处安装整流板来减小局部阻力，并讨论了整流板的安装位置及整流板型式。Zhang和Li等人[9]采用在并联管路的入口安装整流板的措施降低支管阻力，确定了整流板的最佳形式和位置。Gao等人[10]仿生植物分枝，分析突出结构的阻力机理，得出有突出结构的三通管阻力明显降低。张婉卿等[11]对分水器三通管路进行优化设计，指出在二次流区域安装导流片可以起到减阻效果。Li等人[12]对弯头与汇流三通组合管中减阻部件的形状进行了研究，得到椭圆形部件减阻效果最好，指出减阻部件形式与流态有关。

上述研究表明，三通管中由于回流区产生较大的局部阻力，通过安装整流板、减阻部件等措施可有效减阻。整流板是安装某一特定板状装置，通过消除漩涡、减小截面流动不均匀性，从而达到改善流动状态、降低流动损失的目的，多用于大直径弯管或烟道转向室等场合。减阻部件多为翼形或椭圆形等非板状装置，其通过改善内部流动达到降低局部阻力的效果，多用于小管径管道或小空间的场合。通常T型分流三通侧支管回流区面积较大，而在其内部安装整流板来减阻的研究较少。为此，本文以某电厂热一次风管道中分流三通为物理模型，并通过能量耗散分析，得到整流板形式及尺寸对分流三通管阻力特性的影响，旨在为大直径分流三通管的结构优化提供指导。

1 数值模拟

1.1 物理模型

为便于后续分析，定义三通管上游段为主管，下游垂直段为侧支管，下游水平段为直支管，流量比q为侧支管与直支管质量流量之比，高径比h为整流板高度H与侧支管内径之比，长径比l为整流板长度S1与侧支管内径之比。

图1 为三通管道几何模型，管内流体为370 ℃的高温空气，入口流速为11.35 m/s。主管和直支管管径相同，为1 812 mm，侧支管管径为1 308 mm。为排除入口及出口对计算结果的影响，三通管的上游及下游管长均为20倍管径。为保证计算域内流体处于充分发展状态，监测数据截面选取在三通管上游2倍管径和下游12倍管径处[13]。

图1 三通管道几何模型Fig.1 Geometric model of the pipe tee

图2 为不同形式整流板几何模型，其中方案2和方案1的前缘与尾缘尺寸参数相同，与S面相切。方案2和方案3前缘面弧度根据内部流线确定，整流板的几何参数见表1。

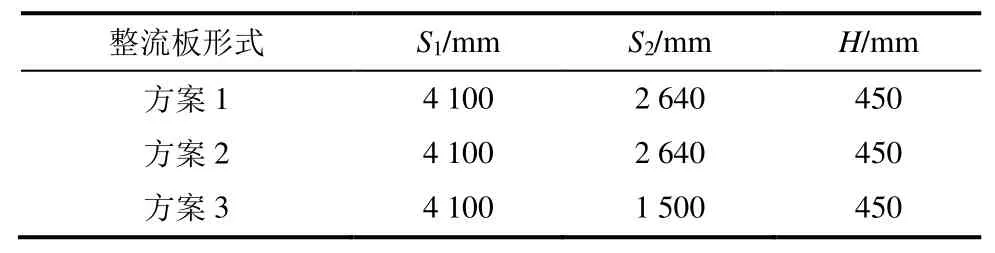
表1 整流板的几何参数Tab.1 Size parameters of various rectifier plates

图2 不同形式整流板几何模型Fig.2 Geometric models of different types of the rectifier plates

为简化计算做以下假设：1）流动为不可压缩的稳态湍流，入口流场均匀，不存在漩涡；2）忽略流体间的换热影响，始终保持在370 ℃。

1.2 网格划分

采用ICEM对三通管道几何模型进行网格划分，如图3所示。

图3 三通管道网格示意Fig.3 Mesh generation of the pipe tee

为提高计算精度和速度，在三通管的上游和下游生成结构化网格，利用O型剖分提高网格质量，在三通处采用非结构化网格进行局部加密。结构网格与非结构网格通过Interface传递数据。近壁面区域采用标准壁面函数法，因此需要考虑第1层网格高度对计算结果的影响，取y+=30[14]，可得第1层网格高度为3.6 mm。

1.3 边界条件及求解器的选择

进口采用速度入口，空气流动方向垂直于入口截面。出口边界采用outflow。操作压力为标准大气压，参考点为侧支管出口的中心点。管壁采用无滑移壁面边界条件，即认为紧贴壁面的流体流速与壁面速度相等，管材为新无缝钢管，绝对粗糙度选取0.06 mm[15]，忽略重力对计算结果的影响。

计算模型选择带有旋流修正的Realizablek-ε湍流模型。基于稳定湍流假设，采用稳态求解器进行数值计算，压力和速度耦合采用SIMPLEC算法[6]。当各项参数残差均小于10–4，进出口流量偏差小于0.1%时，认为计算结果收敛。

1.4 局部阻力系数及能量耗散

三通管道局部阻力系数计算公式为[8,16]：

式中：ζ01为主管与侧支管的局部阻力系数；ζ02为主管与直支管的局部阻力系数；p为静压；ρ为流体密度；u0、u1、u2分别为主管、侧支管、直支管监测截面处的平均流速；λ为沿程阻力系数，当4 000＜Re＜105时，λ=0.316 4/Re0.25，当105＜Re＜3×106时，λ=0.003 2+0.221Re–0.237；δ为减阻率；ζa为原结构局部阻力系数；ζv为加整流板后局部阻力系数。

能量耗散表示机械能转化为热能而造成能量损失，其包括黏性耗散φμ和由于速度脉动引起的湍流耗散φtur[17]。本文采用能量耗散对三通管的损失进行分析，计算模型为：

由于雷诺时均法（RANS）计算结果为时均值，无法获得脉动参数。根据Kock[18]假设可得到

式中ε为湍流耗散率。

1.5 模型准确性验证

采用数值模拟方法对物理问题求解时，需排除网格密度对计算结果的影响。图4给出了不同网格密度下原结构侧支管的局部阻力系数。由图4可见，当网格数为162万时，其局部阻力系数与237万网格计算结果十分接近。考虑到计算精度与模拟时间，采用网格数量为162万的网格密度对该模型进行数值计算，其他模型也以此确定网格密度。

图4 网格密度对计算结果的影响Fig.4 Effect of mesh density on the calculation results

石喜等[4]对PVC三通管进行实验研究，得到不同分流比下的局部阻力系数。采用本文的计算方法对其进行数值模拟，并与其进行比较，结果如图5所示。由图5可见，模拟值与实验值吻合良好，其最大偏差为3.6%。因此，本文选取的计算方法可以反映三通管内的流动特征。

图5 局部阻力系数随流量比q的变化Fig.5 Variations of local resistance coefficient with flow ratio q

2 结果与分析

2.1 整流板形式影响

2.1.1 内流特征

图6 为安装不同形式整流板三通管处流场。由图6可见：未安装整流板时，在侧支管的背流侧形成大面积低速回流区，这是侧支管局部阻力较大的主要原因[4]；安装整流板后，侧支管内回流区面积明显减小，其主要集中在整流板尾缘，而侧支管迎流侧及直支管内流动状态几乎不变。方案1和方案2整流板尾缘的低速区面积较大，这是因为整流板尾缘几何形变较大，使流体与整流板发生分离所致。方案3整流板后低速回流区面积较小，流场相对均匀，流动状态改善效果较好。

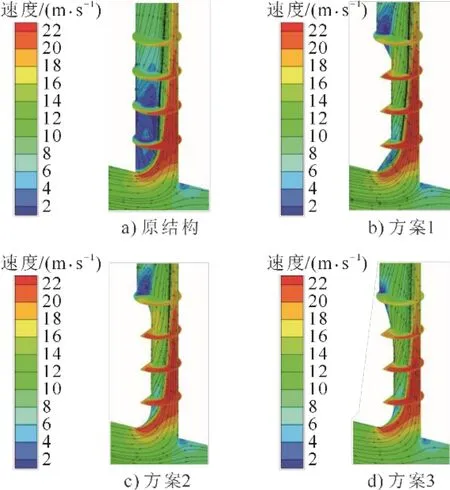
图6 安装不同形式整流板三通管处流场Fig.6 Flow fields of pipe tees with various rectifier plates

2.1.2 阻力特性

三通管道的内流特征直接影响其阻力特性。图7为不同方案三通管局部阻力系数随流量比q的变化。由图7可见，安装不同形式的整流板后，局部阻力系数ζ01均有不同程度降低，而直支管局部阻力系数ζ02基本不变。其中方案3的ζ01最小，且其随流量比先减小后增大。当q=0.2时，方案3侧支管局部阻力系数略大于方案2，这是因为流量比较小时，侧支管内回流区面积较大，方案2整流板影响范围较大，使得方案2侧支管局部阻力系数较小。已有研究表明，弯管与分流三通管道中椭圆形减阻部件效果最好[12]，而在分流三通中，由于方案2整流板高度较高，引起流体脱落，在其尾部形成了低速回流区（图6c)），增大了局部阻力。

图7 不同方案三通管局部阻力系数随流量比q的变化Fig.7 Variations of local resistance coefficient with flow rate q of the pipe tees with different rectifier plates

2.1.3 能量耗散分布

流体流入侧支管时，产生明显变形，通过能量耗散图即可显示损失产生位置。图8为不同方案三通管的能量耗散分布。

图8 不同整流板三通内部能量耗散分布Fig.8 Energy dissipation of pipe tees with different rectifier plates

由图8可见，分流三通管中侧支管背流侧能量耗散较大，能量耗散最大值在侧支管入口中间处，在垂直于流体的流动方向，能量耗散分布呈“月牙”形，且沿流动方向“月牙”逐渐减小。添加整流板后，侧支管入口处能量耗散明显减小，而方案1和方案2整流板尾缘处能量耗散值较大，其主要是因为整流板尾缘坡度较大，形成低速回流区使能量耗散增大。方案3中侧支管入口处流动状态与方案2几乎相同，整流板尾缘能量耗散值较小。

2.2 整流板高度影响

2.2.1 阻力特性

上述研究表明，方案3的减阻效果最好。因此，选择方案3探究整流板高度对局部阻力的影响。图9为侧支管局部阻力系数和减阻率随高径比h的变化。由图9可见，在h＜0.42时，当流量比q较小时，侧支管局部阻力系数ζ01随整流板h增加而减小；q较大时，随h增加，ζ01先减小后增大，且随q增加，ζ01最小值对应的整流板高度降低。图9b)显示，流量比q较小时，减阻率δ随整流板高径比h的增加而增大；q较大时，随h增加，δ先增大后减小，减阻率最大为40.6%。这是因为当q较小时，侧支管内回流区面积较大，使局部阻力系数随整流板高度增加而降低；而当q较大时，回流区面积减小，整流板高度大于回流区宽度导致局部阻力增加。

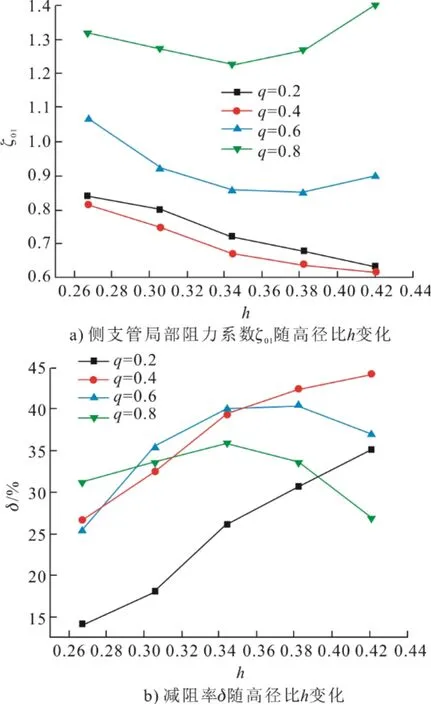
图9 侧支管局部阻力系数和减阻率随高径比变化Fig.9 Variations of local resistance and drag reduction rate with h of side branch pipe

已有研究表明，在弯管与汇流三通的组合管中，减阻部件h=0.25时减阻效果最好[7]。对于分流三通，其侧支管内回流区面积相对较大，当h=0.38时，其减阻效果最好，减阻率为40.6%。

2.2.2 能量耗散分布

图10 为安装不同高度整流板三通管的能量耗散分布。由图10可见，整流板高度较低时能量耗散主要集中在管道中间位置，主要由于流体进入侧支管时发生变形引起；整流板高度较高时，能量耗散主要在整流板尾缘处，主要由于高度较高引起尾缘流体脱落，使整流板尾部形成低速回流区，引起了能量耗散增加。

图10 安装不同高度整流板时三通管内的能量耗散分布Fig.10 Energy dissipation distribution of pipe tees with different heights of rectifier plates

2.3 整流板长度影响

2.3.1 阻力特性

为探究整流板长度对局部阻力的影响，改变方案3中整流板长度，图11为侧支管局部阻力系数和减阻率随整流板长径比l的变化。由图11可见，整流板长度对局部阻力系数影响较小。在l＜3.9时，当流量比q较小时，侧支管局部阻力系数ζ01随整流板长径比l增加而减小；当q=0.6时，随l增加，ζ01先减小后趋于不变；当q较大时，ζ01随整流板长度增加而略微提高。

图11 侧支管局部阻力系数和减阻率随长径比的变化Fig.11 Variations of local resistance and drag reduction rate with l of side branch pipe

图11 b)显示，当流量比较小时，减阻率δ随整流板长径比l增加而增大；q=0.6时，随整流板长度的增加，δ先增大后减小，减阻率最大值为40.2%；当流量比较大时，δ随整流板长度增加而减小。这是因为流量比较小时，侧支管回流区面积较大，增大整流板长度可减小回流区面积，使局部阻力降低；随流量比增大，回流区面积减小。增大整流板长度，减小了下游流通面积，对下游流动状态产生影响，从而增大了阻力。

2.3.2 能量耗散分布

图12 为安装不同长度整流板时三通管内的能量耗散分布。由图12可见，整流板长径比l对三通管的能量耗散影响较小。l较小时，侧支管中间能量耗散略大；l较大时，整流板尾缘的能量耗散略大。因此，随整流板长度增加，侧支管中间能量耗散减小，整流板尾缘处能量耗散增大。安装整流板后，侧支管局部阻力由侧支管入口处和整流板尾缘的能量耗散共同决定。

图12 安装不同长度整流板时三通管内的能量耗散分布Fig.12 Energy dissipation distribution of pipe tees with different lengths of rectifier plates

3 结 论

1）安装整流板后，改善了侧支管内的流动状态，局部阻力系数显著减小，其中方案3减阻效果最好。直支管内流特征及局部阻力系数几乎不变。

2）整流板高度对局部阻力特性影响较大。在h<0.42范围内，当流量比q较小时，侧支管局部阻力系数ζ01随整流板高径比h的增加而减小；q较大时，随h增加，ζ01先减小后增大，其中h=0.38时减阻率最大，达到40.6%。随q增加，局部阻力系数最小值对应的整流板高度降低。

3）整流板长度对局部阻力影响相对较小。在l＜3.9范围内，当流量比较小时，侧支管局部阻力系数ζ01随整流板长径比l增加而减小；当q=0.6时，随l增加，ζ01先减小然后趋于不变，其中l=3.13时减阻率最大，其值为40.2%；当流量比较大时，ζ01随l增加而略微增大。

4）随整流板高度和长度的增大，侧支管入口处能量耗散减小，整流板尾缘处能量耗散增大，两者共同决定ζ01的变化。