基于多策略分区勘探粒子群算法的主蒸汽温度优化控制

刘 萌，王印松，牟文彪，杨 敏，陆 陆

（1.华北电力大学控制与计算机工程学院，河北 保定 071000；2.浙江省能源集团有限公司，浙江 杭州 310007；3.浙江省火力发电高效节能与污染物控制技术研究重点实验室，浙江 杭州 310000）

随着火电机组深度调峰技术的推广应用和新能源发电的大批量并网，火电机组日负荷曲线常处于多峰波动状态，且机组升降负荷速率较快。为满足火电机组快速深度变负荷工况下主蒸汽温度控制器参数整定的需求[1]，各种智能优化算法被应用在主蒸汽温度控制器优化研究，如粒子群（PSO）算法[2]、遗传算法[3]、多目标遗传算法NSGA-Ⅱ[4]、差分进化算法[5]、云模型理论[6]及细菌觅食算法[7]等。这些算法不仅要保证参数优化精度，还需要考虑算法收敛时间是否适应机组快速变负荷的性能要求[8]。

PSO算法作为一种基于迭代寻优的智能优化算法，在参数优化中得到广泛应用[9]。文献[10]提出带有自适应学习因子的PSO算法，在算法进化不同阶段，通过改变因子c1与c2来动态调整PSO的个体认知和全局认知。仿真结果表明改进后算法较标准PSO算法具有更优收敛精度；但改进后算法在提高全局搜索能力的同时降低了算法局部收敛的快速性，整体收敛时间与标准PSO算法区别不明显。文献[11]提出一种自适应权重PSO算法，根据非线性函数动态调整参数，在搜索前期增加粒子全局搜索能力，搜索后期增加粒子局部搜索能力。仿真结果表明，改进后算法收敛精度较标准PSO算法有较大改善；但改进后算法进化前期收敛时间较长，进化后期收敛时间较短，整体收敛时间较标准PSO算法并无明显提升。文献[12]将标准PSO算法中个体最优值采用所有个体最优值，提出扩展PSO算法。扩展PSO算法利用所有个体最优值信息，在算法进化过程中更充分地进行信息共享，从而提高了算法的收敛精度。但扩展PSO算法需要在每次迭代过程计算所有个体最优值，使得收敛时间比标准PSO算法长。文献[13]提出一种混沌PSO算法，该算法使PSO算法摆脱局部最优值，在光伏电站无功优化应用中取得较好效果，但混沌PSO算法引入混沌搜索机制，增加了算法迭代运行数据处理量，在算法收敛速度上不具备优势。

本文将遗传算法中选择算子、自适应学习因子和自适应惯性权重系数多种策略同时引入标准PSO算法，通过不同分区测试，将各算子优势充分体现，提出基于多策略分区勘探PSO算法。并采用所提出算法优化火电机组主蒸汽温度控制器参数，仿真结果验证了本文算法的有效性。

1 问题描述

火电机组主蒸汽系统简化流程如图1所示，主蒸汽温度喷水减温串级控制系统如图2所示。图2中：TSP为主蒸汽温度设定值，TPV为主蒸汽温度测量值，WP为过热器减温水喷水流量，GC1(s)为主环控制器，GC2(s)为副环控制器，G2(s)为导前区传递函数，G1(s)为惰性区传递函数[14]。

图1 火电机组主蒸汽系统简化流程Fig.1 The simplified flow chart of main steam system in thermal power unit

图2 主蒸汽温度喷水减温串级控制系统Fig.2 The cascade control system of spray desuperheating for main steam temperature

机组运行过程中，需要控制给煤量与给水量并使之处于动态平衡状态，根据给水量和给煤量改变的先后顺序，可分为水跟煤和煤跟水2种控制方式。由于汽水分离器出口过热蒸汽温度能够较灵敏地反映水煤比的变化，常称为中间点温度，实际应用中，常采用水煤比粗调、喷水减温细调的串级PID控制。随着火电机组快速深度变负荷技术的推广应用，火电机组常处于快速变工况运行，为使得控制器性能最优，需要根据在线辨识后的模型不断更新控制器参数。

当火电机组处于深度调峰快速变负荷运行工况，升降负荷速率常达到1%~2%，部分先进机组可以达到2%~4%，机组负荷可以在2.5~5.0 min内变化10%[15]。因此，针对火电机组快速深度变负荷工况下的主蒸汽温度控制器参数的寻优，寻优算法不仅需要具备寻优精度高和跳出局部极值的能力，还需具有较快的收敛时间，保证在机组快速变负荷工况中始终运行在最优控制器参数，这对提高机组整体能量利用效率和安全稳定运行具有重要意义。

2 多策略分区勘探PSO算法

2.1 算法描述

PSO[9]算法结构简单，参数易调整，算法迭代寻优过程中粒子位置更新及粒子速度更新的计算分别为：

式中：vi为粒子速度，zi为粒子位置，w为惯性权重系数，c1和c2为学习因子，rand为0~1之间随机数，pi为粒子自身搜索到的最优解，pg为群体搜索到的最优解。

标准PSO算法的寻优策略比较单一，并且w、c1、c2为固定参数，具有较大的改进空间。遗传算法中选择算子建立在对个体的适应度进行评价的基础上，淘汰对算法无意义或影响很小的个体，由此提高计算效率和加快算法收敛速度，但同时也破坏了群体的多样性，使算法容易过早陷入局部极值。自适应学习因子PSO[10]（ALFPSO）算法根据当前迭代次数采用一种自适应调整学习因子c1、c2的非线性方法，具有较强的全局搜索能力，但同时也造成算法收敛时间的增加。文献[11]指出，较大的w值有利于跳出局部极值，较小的w值有利于算法收敛，动态惯性权因子PSO（DIWPSO）算法的主要思想是在更新粒子速度时，根据当前迭代次数对原有速度加入一种压缩系数，使算法进化的不同时期具有不同的寻优特性。

为了兼顾上述几种算法在收敛精度和收敛时间方面的优势，针对火电机组主蒸汽温度系统控制器参数寻优，本文提出了一种多策略分区勘探PSO（MSZPSO）算法，该算法描述如下：

1）迭代第k（k＞1）步，将种群中粒子根据个体适应度pi进行升序排序。

2）将a%~b%区间（a∈R、b∈R且50＜a＜b＜100）作为选择算子操作区，将a%~b%区间内粒子替换为(100-b)%~(100-a)%区间的粒子，即将选择算子操作区内的低劣适应度个体替换为优良适应度个体。

3）将c%~d%区间（c∈R、d∈R且0＜c＜d＜100）作为自适应学习因子操作区，根据式(3)、式(4)、式(5)更新参数c1、c2，其中t为当前迭代次数、M为算法设定最大迭代次数。

4）将e%~f%区间（e∈R、f∈R且0＜e＜f＜100）作为自适应惯性权因子操作区，根据式(6)更新参数w，其中wmin为初始惯性权重系数、wmax为终止惯性权重系数。

MSZPSO算法整体流程如图3所示。

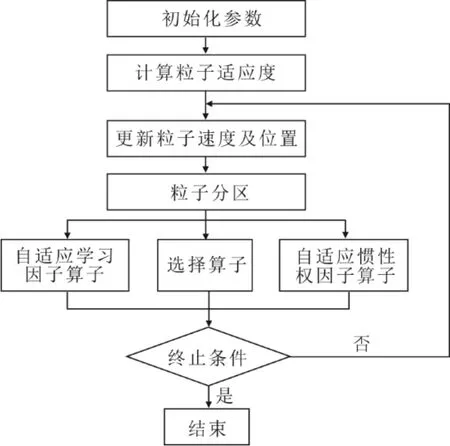
图3 MSZPSO算法流程Fig.3 Flow chart of the MSZPSO algorithm

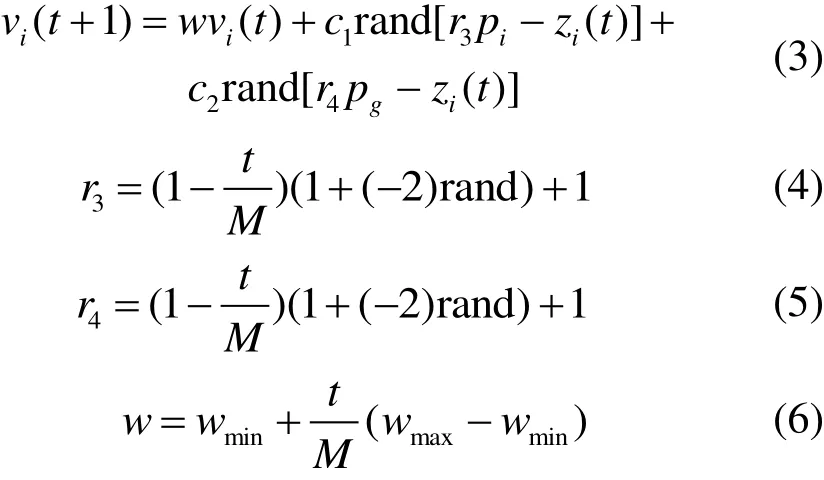
2.2 算法策略分析

MSZPSO算法是在标准PSO算法基础上加入选择算子、自适应学习因子和动态惯性权因子，通过粒子个体适应度分区勘探的策略以保证算法具有较高收敛精度，同时具有较快的收敛速度。根据图3所示，MSZPSO算法需要设定的变量有选择算子操作区间a%~b%、自适应因子操作区间c%~d%、自适应惯性权重系数操作区间e%~f%、学习因子c1和c2、初始惯性权重系数wmin、终止惯性权重系数wmax。选择算子不产生新的算子，其作用是加速算法收敛，自适应学习因子和自适应惯性权重系数的作用均是增加粒子群体的多样性，避免算法陷入局部最优。因此，为平衡3种算子之间的关系，提高算法综合性能，划分合适的算子操作区间是关键。

设定MSZPSO算法中粒子数目N为80，算法最大迭代次数M为5 000，学习因子c1=c2=2.0，初始惯性权重系数wmin=0.9，终止惯性权重系数wmax=0.2，选择算子操作区间（SO）、自适应学习因子操作区间（ALFO）和自适应惯性权重系数操作区间（AIWF）选取8种（s1~s8）不同区间（表1）。实验选取10种基准测试函数（表2），设定各测试函数维度D=50。采用各测试函数分别独立运行100次，实验中当全局最优适应值与理论最优值之差的绝对值小于10–10，则认为算法求得最优解，TV表示求得最优解的次数，AM表示搜索到最优解的平均迭代次数，SDM表示最优解迭代次数的标准差。若算法在某次运行迭代终止时，全局最优适应值与理论最优值之差的绝对值大于10–10，则该次结果不计入TV和SDM的运算。若算法运行100次均未求得最优解，则用MBF表示算法平均最优适应值，SD表示最优适应值的标准差。8种分区测试实验数据见表3，同一函数中每组实验标准的最优值用粗体表示。

表1 8种操作区间的划分 单位：%Tab.1 Division of 8 operation intervals

表2 10种基准测试函数Tab.2 Information of 10 benchmark functions

根据表3，MSZPSO算法在D=50维基准函数f1、f2、f3、f5、f6、f7、f8、f9均可取得满足精度要求的解，且不同的分区对算法性能有较大的影响。针对选择算子分区，当选择算子操作区间（SO）范围较大时，算法容易过早收敛，成功寻优的次数较小，但具有较少的平均迭代次数；当增大自适应学习因子操作区间（ALFO）分区，算法成功寻优次数有所提高，但平均迭代次数略微增加；自适应惯性权重系数操作区间（AIWF）主要影响算法的最优解迭代次数的标准差，当选择较小的AIWF区间，在不影响算法寻优解次数下，可以使得算法SDM有所降低，使算法具有更可靠的寻优性能。当算法选择s4区间参数时，可以在10种基准函数的28类指标中取得10类最优指标，算法拥有较好的优化性能，因此本文选取s4区间作为后续仿真实验中的MSZPSO算法参数。

表3 8种分区测试实验数据对比Tab.3 The experimental data of 8 partition tests

3 仿真实验

3.1 MSZPSO算法与其他算法比较

为验证本文所提算法有效性，将MSZPSO算法与4种改进PSO算法及标准PSO算法进行基准测试函数寻优对比，4种改进PSO算法分别为自适应学习因子粒子群（ALFPSO）算法[10]、自适应动态惯性权重系数粒子群（DIWPSO）算法[11]、扩展粒子群（EPSO）算法[12]和混沌粒子群（ChPSO）算法[13]。实验结果见表4，表4中各指标最优值用粗体表示。

实验基准测试函数见表2，设定各测试函数维度D=100，粒子数目N=80，算法最大迭代次数M=10 000，学习因子c1=c2=2.0，初始惯性权重系数wmin=0.9，终止惯性权重系数wmax=0.2，各改进PSO算法参数按照原文献设置。各算法独立运行100次，用MBF表示平均最优适应值，SD为最优适应值标准差，Tt表示算法平均寻优时间，单位s。

根据表4数据可得：标准PSO算法参数固定且不加入额外运算，算法收敛时间在6种算法中较好，但早熟收敛问题也最为突出。ALFPSO、DIWPSO、EPSO算法均在收敛精度上较标准PSO算法有所提高，但这3种算法收敛时间指标均劣于标准PSO算法。ChPSO算法引入混沌搜索机制，在函数f10取得6种算法中唯一理论最优解，但算法收敛时间是标准PSO算法的3~5倍。MSZPSO算法在函数f1、f2、f3、f5、f6、f7、f8均求得理论最优解，在函数f4、f9、f10取得次最优解；在函数f1、f2取得比其他5种算法更短的寻优时间，在函数f3、f4、f6取得次最短寻优时间，MSZPSO算法共计在所有指标中取得16次最优和8次最优，同时兼顾了收敛精度和收敛时间。

表4 MSZPSO算法与其他5种PSO算法100维实验数据对比结果Tab.4 The 100-dimensional test results of the MSZPSO algorithm and five other PSO algorithms

3.2 主蒸汽温度控制系统仿真实验

基于MATLAB平台，对比PSO、ALFPSO、DIWPSO和MSZPSO算法在主蒸汽温度串级控制系统中PID参数整定的寻优效果，4种算法均以系统输出的绝对误差积分作为个体适应度，控制系统主、副环控制器均采用PI型，如式(7)所示[16]。

式中，Kp为比例增益，Ti为积分时间。

实验采用文献[2]中某火电机组主蒸汽温度系统传递函数模型与仿真参数，在62%负荷工况下进行主蒸汽温度定值扰动实验，分别采用PSO、ALFPSO、DIWPSO和MSZPSO算法进行控制器参数寻优，设置粒子数目N=40、最大迭代次数M=1 000、仿真时间TK=1 000 s，各算法收敛对比曲线如图4所示，最优输出响应对比曲线如图5所示，动态性能指标对比见表5，控制器参数对比见表6。

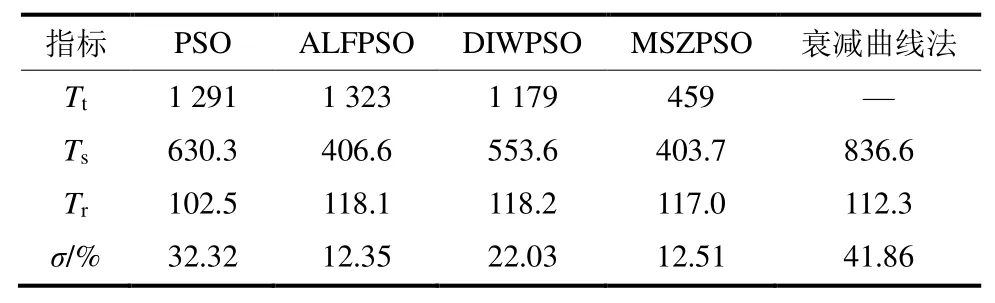
表5 动态性能指标对比1Tab.5 Dynamic performance index comparison 1

表6 控制器参数对比Tab.6 Comparison of the controller parameters

图4 算法收敛比较Fig.4 Convergence comparison of the algorithms

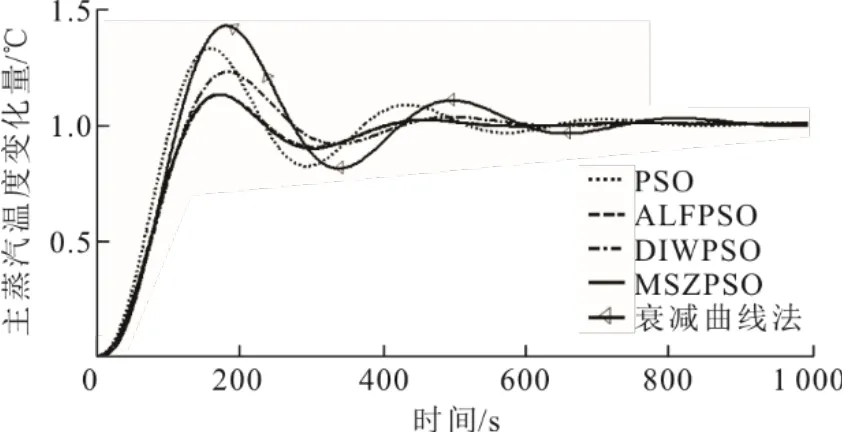
图5 算法最优输出响应曲线Fig.5 The optimal output response curves of algorithms

表5 、表6中：Tt为算法寻优时间，s；Ts为算法最优输出响应调节时间（误差范围取稳态值±2%），s；Tr为最优输出响应上升时间，s；σ为最优输出响应超调量；Kp1为主环控制器比例增益；Ti1为主环控制器积分时间；Kp2为副环控制器比例增益；Ti2为副环控制器积分时间。

由图4可见：MSZPSO算法加入自适应学习因子和自适应惯性权因子，能够避免过早陷入局部最优，具备良好的全局搜索能力。由图5可见：PSO、ALFPSO、DIWPSO和MSZPSO 4种算法均取得较衰减曲线法更好的控制器性能。其中，MSZPSO算法对应的调节时间、超调量、寻优时间指标均优于PSO、DIWPSO算法。由于MSZPSO算法加入了选择算子，使算法可以在每次迭代过程中淘汰适应度较大的个体，避免求取个体适应度时积分运算使数据处理过于庞大，提高了算法的执行效率。因此，在调节时间、超调量指标接近情况下，MSZPSO算法寻优时间仅为ALFPSO算法的38.93%，综合寻优性能优于PSO、ALFPSO和DIWPSO算法。

采用机组负荷为44%的模型参数，控制器采用表6中参数，主蒸汽温度扰动响应曲线如图6所示，动态性能指标对比见表7。由图6和表7可见，当模型参数改变时，在4种算法中，MSZPSO算法系统输出的调节时间最短，超调量最小。

图6 系统模型改变时系统动态响应Fig.6 The dynamic response when the system model changes

表7 动态性能指标对比2Tab.7 The dynamic performance index comparison 2

综合上述仿真结果表明，MSZPSO算法基于多策略分区勘探，使算法同时兼顾选择算子、自适应学习因子和自适应惯性权因子的优势，在寻优过程中能够兼顾收敛精度和收敛时间的要求。同时，当系统参数改变时，能够较其他3种算法取得更好的控制效果。

4 结 论

1）基于多策略分区勘探设计理念，将选择算子、自适应学习因子、自适应惯性权重系数通过合适的分区，能够使得算法同时具有较高寻优精度和较短收敛时间。

2）本文所提改进算法较多种改进PSO算法更适合机组快速变负荷工况下的参数优化，并可推广应用至其他类似约束下PID参数整定问题。