提升初中生几何证明题的方法

普布德吉

（西藏拉萨市堆龙德庆区中学，西藏 拉萨 851400）

进行几何证明，主要要求初中生严谨规范、条例清晰、结论明确。而且，几何推理的明确性与条理性，解题的严谨性与完备性都是几何问题和抽象思维的一种逻辑阐述。实际教学期间，多数学生都在几何证明问题上失分较多，主要是因为其书写凌乱，推理缺少逻辑性。为此，对提升初中生几何证明题的方法展开探究有着重要意义。

一、几何书写现存问题

（一）审题粗心

其实，审题是学生大脑提取有关信息的一个重要渠道，借助审题形成初步的解题思路，如果审题错误，必然会导致解题错误。当前，很多初中生都存在审题粗心这个问题，常常忽视问题当中包含的关键字和已知条件，致使解题错误。

（二）书写凌乱

几何证明问题主要讲究整洁，书写过程非常凌乱以及潦草，从侧面反映出了初中生的解题思路并不清晰，而且解题过程出现一些问题，影响教师对于初中生的书写印象，扣除解题过程与卷面分。

（三）书写推理缺少逻辑性

几何证明问题是环环相扣的，推理过程必须有理有据。当前，一些初中生的书写过程非常杂乱，缺少条理性，而且解题思路非常混乱，逻辑语言经常上下不搭，还有一些初中生用尽了题设当中的已知条件，甚至捏造条件进行书写。

二、提升初中生几何证明题的方法

（一）培养初中生的审题能力

第一，增加几何题的阅读训练。日常教学期间，数学教师需指导初中生多读多练，无论课上或是课下，需培养初中生认真阅读这个良好习惯。课堂教学期间，数学教师可带领初中生一边阅读，一边在图形当中标出已知条件，借此帮助初中生对问题进行分析，并且培养初中生良好阅读习惯。进行课后练习期间，同样要求初中生在图形当中标出条件[1]。第二，培养初中生良好审题习惯。进行审题期间，必须逐句读题，同时标出关键条件，这样便于初中生对问题进行直观分析。如果解题遭遇挫折，需反复进行读题，检查是否对所有条件加以充分利用。第三，善于对问题当中一些隐含条件进行挖掘[2]。例如，求证三角形全等之时，等腰三角形的三线合一、公共边、公共角与顶角通常为解题关键。针对综合性较强的问题，数学教师需指导初中生对已知条件加以适当迁移与转化，进而找到解题入口。

（二）重视例题教学，培养初中生的书写习惯

日常教学期间，数学教师需示范条件清晰并且严谨明确的例题示范，进而培养初中生良好的解题习惯。

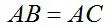
证法一：

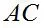
设∠1=∠FMB，∠2=∠ACB，∠3=∠BCE，∠4=∠FMD

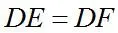
（三）掌握基本内容，让证明过程逻辑严谨，条理清晰

实际上，几何证明好比写逻辑性非常强的文章，需要思考先写什么，之后写什么，所有步骤如何写才是科学的、简洁的，这些全都有一定讲究。所以，几何证明变成初中生的一个学习难点。教学期间，数学教师需让初中生对基本概念、定理与公理进行掌握，让证明过程逻辑严谨，条理清晰，进而为其攻克难题奠定基础[3]。

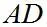
分析：此题是对相似三角形的性质加以考查，需要学生对圆的定义和具体性质加以掌握。

结论：综上可知，西藏地区的初中生由于存在一定的语言障碍，缺少良好的审题习惯，书写非常凌乱，缺少逻辑性，导致其在几何证明问题方面失分较多。为此，教学期间，数学教师需培养初中生的审题能力，重视例题教学，培养初中生的书写习惯，同时掌握基本内容，让证明过程逻辑严谨，条理清晰，有效提升初中生的解题能力与解题效率。