一类拟线性双曲型方程Cauchy 问题经典解的整体存在性
周苗苗,聂大勇
(1.华北水利水电大学 数学与统计学院,河南 郑州 450046;2.黄河水利职业技术学院,河南 开封 475004)
0 引言
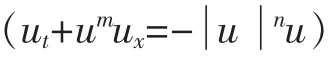

其中,特征λ(u)=um;非齐次项f(t,x,u)=-un+1;m,n 是非负整数;初始条件ϕ(x)∈C1,且C1模有界。
1 两类特殊情形
1.1 低阶耗散情形
当n=0 时,式(1)可变为式(2)。

其中,m≥1,ϕ(x)∈C1,且C1模有界。
定理1 假设初始数据ϕ(x)的C1模充分小,则Cauchy 问题(2)在上半平面t≥0 上存在唯一的整体经典解[6]。
对上半平面t≥0 上任意点(t,x),向下做特征线x 轴于(0,α),它满足式(3)所示的条件。沿特征线x=x(t,α),存在式(4)。 由此即得式(5)和式(6)。

对式(2)的第一式沿特征线关于x 求导,得到式(7)。 由于ux(0,x)=ϕ′(x),求解得式(8)。
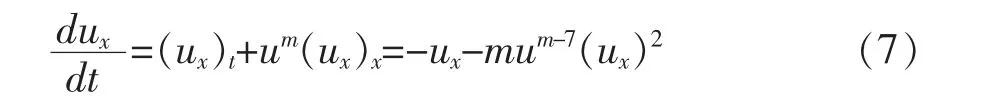

1.2 线性退化情形m=0
具线性退化特征(λ′(u)=0)的拟线性双曲型方程的Cauchy 问题为式(9)。

其中,n>0,ϕ(x)∈C1,且C1模有界。

引理1 对Cauchy 问题(9),经典解u(t,x)在上半平面t≥0 上保持一致有界的充分必要条件是假设ϕn(x)≥0,∀x∈R。
对式(9)的第一式两端沿特征线关于x 求导,得式(11)。

注意到ux(0,x)=ϕ′(x),得式(12)。
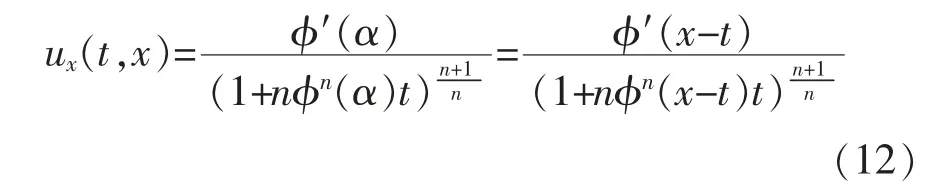
由式(10)和式(12),可得定理3。

2 一般情形
一般情形即考虑m>0,n>0 的情形。
设过点(0,α)的特征线为x=x(t,α),同理可以得到式(14)和式(15)。

引理2 Cauchy 问题(1)经典解u(t,x)的C0模在上半平面t≥0 上保持一致有界的充分必要条件是ϕn(α)≥0,∀x∈R。
定理4 在假设ϕn(α)≥0,∀x∈R 的条件下,有如下结论:
(1) 当m>n 时, 如果初始条件的C1模充分小(实际上只要ϕ′(x) 的C1模充分小即可), 那么Cauchy 问题(1)在上半平面t≥0 上存在唯一的整体经典解。



当m>n 时,如果(ϕm-n(x)) ′≥0,∀x∈R,显然也有A(t,α)>0,因此,在上述条件下,Cauchy 问题(1)在上半平面上也存在整体经典解。
3 结语
本文主要研究了一类拟线性双曲型方程中的非线性特征与非齐次项对Cauchy 问题经典解整体存在性的一些影响,得到了在低阶耗散情形、线性退化情形和一般情形下保证经典解整体存在的充分必要条件,扩充了拟线性双曲型方程Cauchy 问题经典解存在性的相关研究内容,也为流体力学、工程技术和生命科学等领域研究相关模型解的大时间性态提供了理论基础。

