不定方程x3+1=4 781y2解的讨论

朱 哲，管训贵

（泰州学院 数理学院，江苏 泰州 225300）

1 引言及主要结论

不定方程

的整数解已有不少人研究过。柯召、孙琦[1-2]证明了当D＞2，D无平方因子且不含6k+1 型的素因子时，方程(1)无非平凡解。当D含6k+1 型的素因子时，求方程的非平凡解显得尤为困难[3]，其中一类典型的不定方程是

对方程(2)的研究，目前只有一些零散的结果[4-10]。本文利用初等方法给出q=683时方程(2)的解，即证明了如下定理

定理不定方程

仅有整数解(x,y)=(-1,0)。

2 若干引理

引理1[11]20-21设p是一个奇素数，则方程

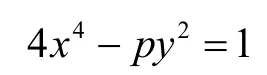
除p=3,x=y=1和p=7，x=2,y=3外，无其他的正整数解。

引理2[11]273-275方程x2-3y4=1仅有整数解

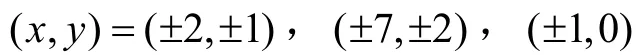
引理3[11]260-261设p是一个奇素数，则方程

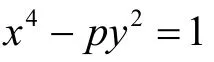
除p=5,x=3,y=4和p=29,x=99,y=1820外，无其他的正整数解。

3 定理的证明

证明因为(x+1,x2-x+1)=1或3，故方程(3)给出8 种情形，如表1 所示。

表1 方程(3)给出的8 种情形

情形Ⅰ由第一式得x≡-1(mod683)，代入第二式得7v2≡3(mod683)，即(7v)2≡21(mod683)，但Legendre 符号

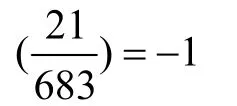
不可能成立，故该情形不定方程(3)无整数解。

情形Ⅱ由第二式得

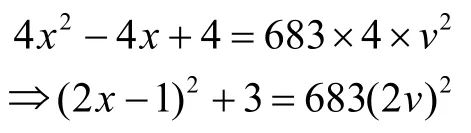
故(2x-1)2≡-3(mod683)，但Legendre 符号

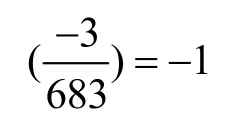
不可能成立，故该情形不定方程(3)无整数解。

情形Ⅲ由第二式得

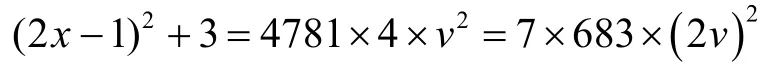
故(2x-1)2≡ -3(mod683)，由情形Ⅱ知，该式不可能成立，故该情形不定方程(3)无整数解。

情形Ⅳ由解第二式得

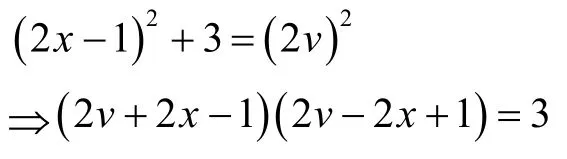
解得x=0,1，均不适合第一式，故该情形不定方程(3)无整数解。

情形Ⅴ由第一式得x≡-1(mod683)，代入第二式得3 ≡21v2(mod683)，即(7v)2≡7(mod683)，但

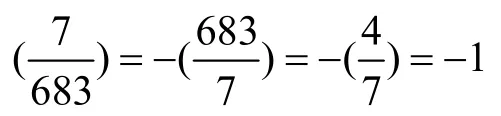
不可能成立，故该情形不定方程(3)无整数解。

情形Ⅵ由第二式得

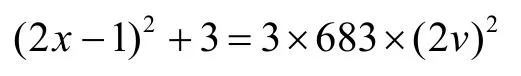
所以(2x-1)2≡-3(mod683)，由情形Ⅱ知，不可能，故该情形不定方程(3)无整数解。

情形Ⅶ由第二式得

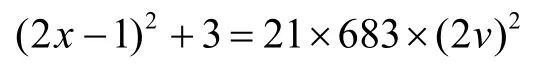
所以(2x-1)2≡-3(mod683)，由情形Ⅱ知，该式不可能成立，故该情形不定方程(3)无整数解。

情形Ⅷ将第一式代入第二式整理得

故有

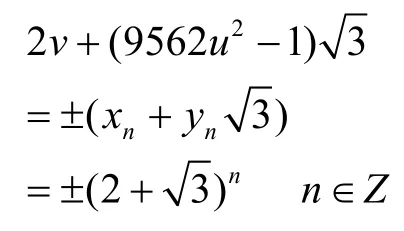
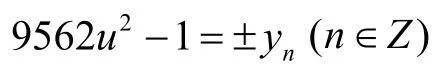
即

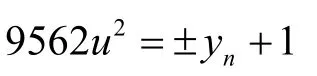
又y-n=-yn，所以只需考虑

可验证下列各式成立：

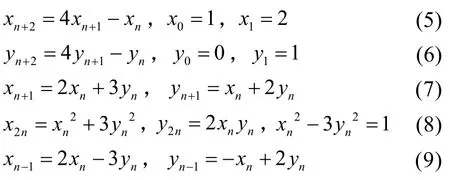
若n≡0(mod2)，则由(6)知yn≡0(mod2)，此时(4)式不成立。

若n≡1(mod4)，令n=4k+1(k∈Z)，则由(7)、(8)可得

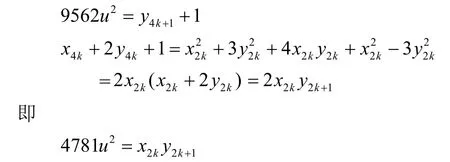
又因

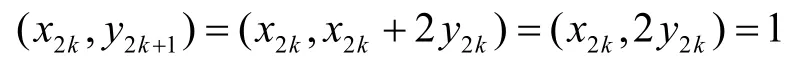
所以下列情形之一成立（u=mh，(m,h)=1）：

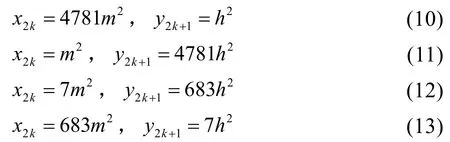
将(11)的第一式x2k=m2代入，得。根据引理3 知，m2=1，即x2k=1，则k=0，但由(6)及(11)的第二式知，y1≠4781h2，所以(11)式不成立。

因x2k≡/0(mod2)，故m为奇数，则m2≡1(mod8)；而y2k+1≡/0(mod2)，故h为奇数，则h2≡1(mod8)。又y2k≡0,4(mod8)，故2y2k≡0(mod8)。对(14)两边取模8，得 -4 ≡0(mod8)，该式不可能成立。

类似(12)式的讨论知，(13)也不可能成立。

若n≡-1(mod4)，令n=4k-1(k∈Z)，则由(7)、(8)、(9)可得

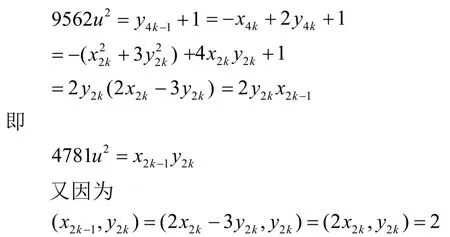
所以下列情形之一成立（u=2mh，(m,h)=1）：

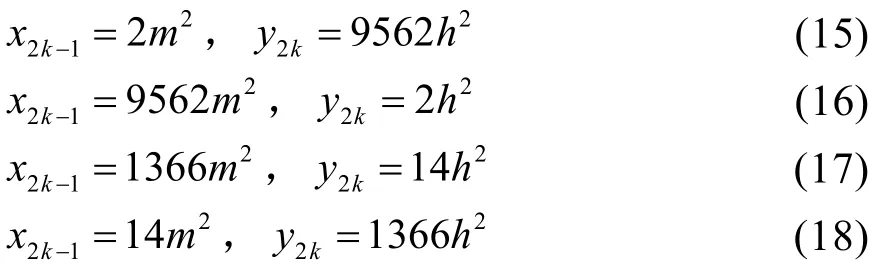
由(16)的第二式得x k y k=h2，因(xk,yk)=1，有xk=a2，yk=b2，故(a2)2-3b4=1，由引理2 知，a2=1，此时xk=1，则k=0，推出(16)的第一式不成立。

由(17)的第二式得x k yk=7h2，因(x k,yk)=1，有

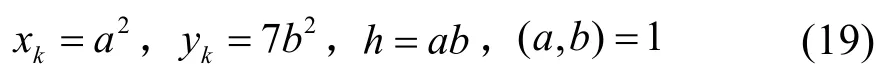
或

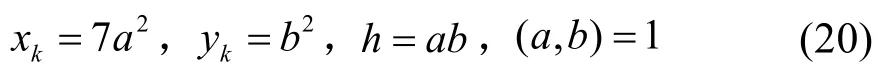
若(19)成立，则有

由引理3 知，方程(21)仅有整数解(a,b)=(±1,0)，此时y2k=0，则k=0，推出(17)的第一式不成立。

若(20)成立，则有

由引理2 知，方程(22)仅有整数解(a,b)=(±1,± 2)，故xk=7，则k=2。此时n=7，所以由(4)，得9562u2=y7+1=2912，该式不可能成立。

由(18)的第二式得x k yk=683h2，因(x k,yk)=1，有

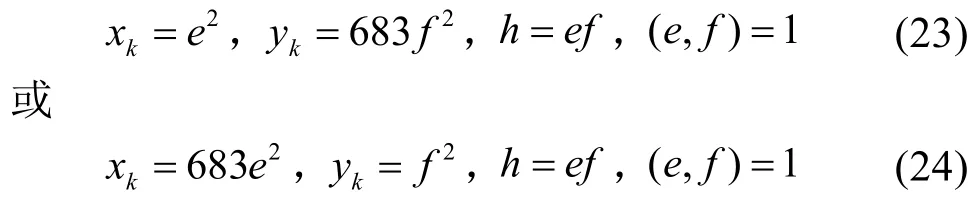
若(23)成立，则有

由引理3 知，方程(25)仅有整数解(e,f)=(±1,0)，此时y2k=0，则k=0，推出(18)的第一式不成立。

若(24)成立，则有

由引理2 知，方程(26)给出683e2=2,7,1，显然不可能。

综上，不定方程(3)仅有整数解(x,y)=(-1,0)，定理得证。