高阶双曲型Kac-Moody 代数的极小虚根

胡建华，刘静，许成苏

（上海理工大学理学院，上海200093）

虚根是不定型Kac-Moody 代数中的一个基本概念，但其结构至今尚未完全弄清楚。双曲型Kac-Moody 代数是一类特殊的不定型Kac-Moody代数，文献[1]给出了所有双曲型广义Cartan 矩阵的分类，总共分为10 类。双曲型Kac-Moody 代数的虚根因具有一些特殊的性质而受到关注。文献[2-6]刻画了Kac-Moody 代数的极小虚根的某些性质。文献[7]给出了三阶双曲型Kac-Moody 代数的所有极小虚根。文献[8]给出了四阶双曲型Kac-Moody 代数的所有极小虚根。本文将在此基础上，给出n(5 ≤n≤10)阶双曲型Kac-Moody 代数的全部极小虚根。这样所有双曲型Kac-Moody代数的极小虚根都被完全刻画出来。

1 重要定义及性质

现给出极小虚根的定义及极小虚根的基本性质，本文中提到的其他相关定义及符号参见文献[8-10]。

性质1[3]ɡ(A)的极小虚根的个数是有限的，ɡ(A)是广义Cartan 矩阵GCMA对应的Kac-Moody代数。

性质5[7]双曲型Kac-Moody 代数ɡ(A)的Dynkin 图的每个Aff 型连通子图确定唯一一个null 的极小虚根。

2 高阶双曲型Kac-Moody 代数的极小虚根

文献[1]给出了所有双曲型GCM 的分类，总共有238 类，其中，有35 个严格双曲型，双曲型GCM 的阶不大于10，严格双曲型GCM 的阶不大于5。现给出5～10 阶双曲型GCM 所对应的Kac-Moody 代数的全部极小虚根。

定理1 五阶双曲型Kac-Moody 代数的极小虚根如表1 所示。

表1 Kac-Moody 代数的极小虚根（Ⅰ）Tab.1 Minimal imaginary roots of Kac-Moody algebra（Ⅰ）

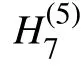
图1 的Dynkin 图Fig.1 Dynkin diagram of type of

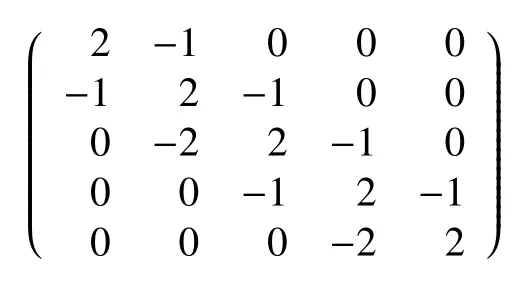
定理2 六阶双曲型Kac-Moody 代数的极小虚根如表2 所示。

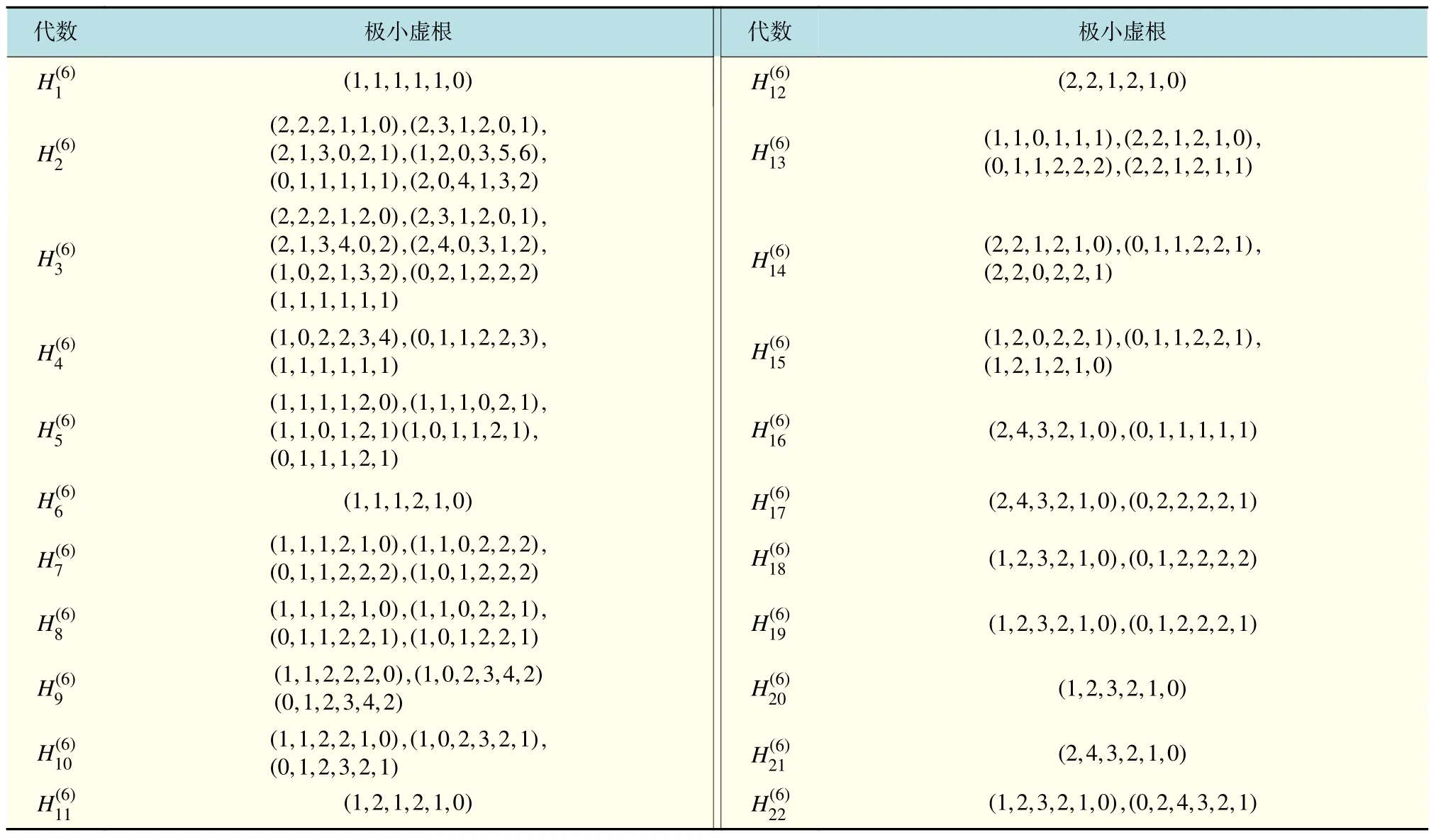
表2 Kac-Moody 代数的极小虚根（Ⅱ）Tab.2 Minimal imaginary roots of Kac-Moody algebra（Ⅱ）

的Dynkin 图如图2 所示。

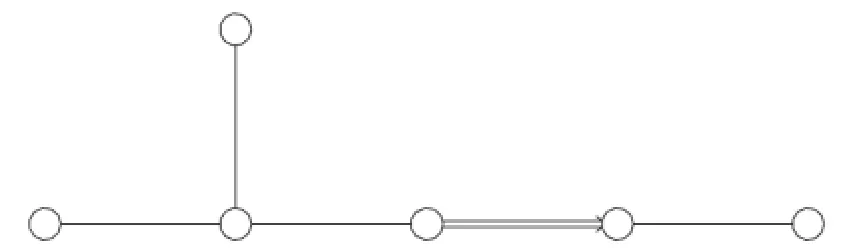
图2 的Dynkin 图Fig.2 Dynkin diagram of type of

的Cartan 矩阵为

的五阶连通真子图中有Aff 型，支集为{α1,α2,α3,α4,α5}，还有2 个Aff 型，支集分别为{α1,α3,α4,α5,α6}，{α2,α3,α4,α5,α6}，由性质5 可知，它们分别唯一确定一个null 的极小虚根，记为β1=(1,1,2,2,2,0)， β2=(1,0,2,3,4,2)，β3=(0,1,2,3,4,2)。的四阶、三阶及二阶连通真子图均是Fin 型，不存在极小虚根。

考虑支集为{α1,α2,α3,α4,α5,α6}的极小虚根。

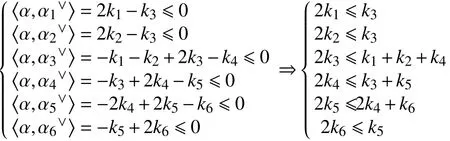
定理3 七阶双曲型Kac-Moody 代数的极小虚根如表3 所示。

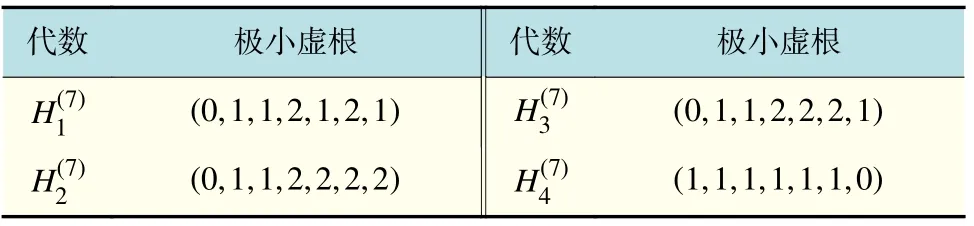
表3 Kac-Moody 代数的极小虚根（Ⅲ）Tab.3 Minimal imaginary roots of Kac-Moody algebra（Ⅲ）

的Dynkin 图如图3 所示。

图3 的Dynkin 图Fig.3 Dynkin diagram of type of

的Cartan 矩阵为

的六阶真子图中有Aff 型，支集为{α2,α3,α4,α5,α6,α7}，由性质5 可知，它唯一确定一个null 的极小虚根，记为β=(0,1,1,2,1,2,1)。的低于六阶的真子图均为Fin 型，不存在极小虚根。

定理4 八阶双曲型Kac-Moody 代数的极小虚根如表4 所示。

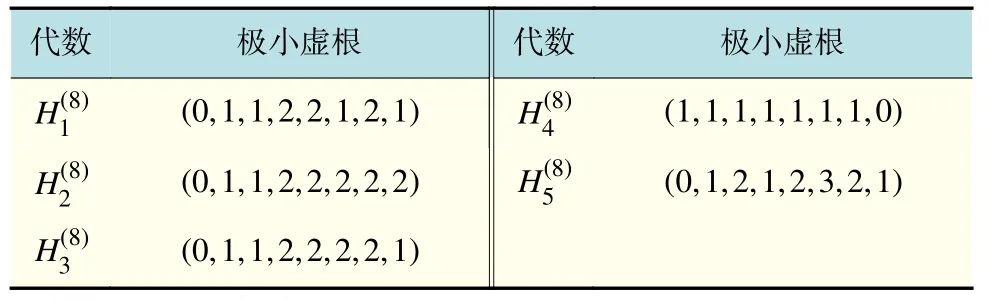
表4 Kac-Moody 代数的极小虚根（Ⅳ）Tab.4 Minimal imaginary roots of Kac-Moody algebra（Ⅳ）

定理5 九阶双曲型Kac-Moody 代数的极小虚根如表5 所示。

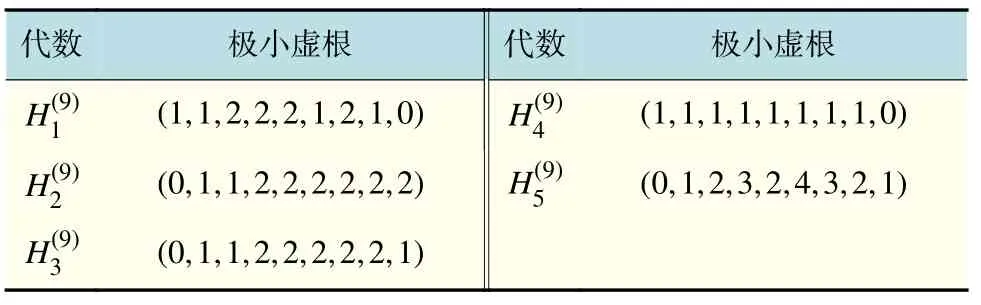
表5 Kac-Moody 代数的极小虚根（Ⅴ）Tab.5 Minimal imaginary roots of Kac-Moody algebra（Ⅴ）

定理6 十阶双曲型Kac-Moody 代数的极小虚根如表6 所示。

表6 Kac-Moody 代数的极小虚根（Ⅵ）Tab.6 Minimal imaginary roots of Kac-Moody algebra（Ⅵ）

定理4～6 的证明过程与定理1～3 的证明过程类似，这里不再证明。

至此，n(5 ≤n≤10)阶双曲型Kac-Moody 代数的极小虚根已经全部给出，再结合文献[5, 7-8]，双曲型Kac-Moody 代数的极小虚根就全部给出了。