决策信息数据为区间数的一种多属性群决策方法

朱国成, 陈利群

(广东创新科技职业学院 通识教育学院, 广东 东莞 523960)

0 引言

目前,对于区间数的多属性群决策问题的研究主要集中在评价专家权重模型的建立[1]、确定属性偏好路径的方法[2]和方案排序的算法[3]等问题上.当属性是成本型和效益型并存时,或者是更多种类型并存时,在计算评价专家权重前均需要对决策数据进行规范化处理[4-6].因为区间数熵值法在确定属性权重时能够较为完整地保留决策信息数据,且计算过程相对简单,所以学者在解决属性偏好问题中多采用该方法.文献[7]针对属性值为区间数的情形,采用区间数熵值法计算了属性权重,并根据各方案的属性优良个数对方案的优劣进行了鉴定,经数值算例表明该方法科学有效;文献[8]利用定义的区间数转换公式将由常数构成的属性值转换为区间数,然后利用区间数的积型贴近度模型构建了一种区间数排序理论,实证结果显示该理论能够取得符合实际的决策效果;文献[9]建立了4种情形下的评价专家权重的计算模型,并提出了一种可行的区间直觉模糊多属性群决策算法.本文受文献[7-9]的启发,建立了一种在求解评价专家权重前无需对属性数据先进行规范处理的求解模型,并提出了一种求解方案有效理想综合测度结果的多属性群决策方法,最后通过实例验证了本文方法的可行性.

1 预备知识

1.1 区间数理论

定义1[10]记a=[a-,a+]={x|a-≤x≤a+,a-≤a+,a-,a+∈R}, 称a为区间数.若0≤a-≤a+, 则称a为正区间数;若a-=a+, 则a退化为实数.

1.2 多属性群决策理论下的相关定义

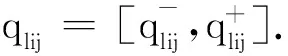
定义6属性的理想属性值的计算方法为:

定义7规范化加权评价表[ωPlqlij]HMN，规范的方法为:

2 决策专家权重及属性权重的计算方法

2.1 决策专家权重的计算方法

根据定义5,计算决策专家权重的步骤为:

步骤1 绘制专家给予方案的评分表[qlij]HMN;

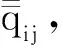
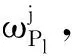
2.2 属性权重的计算方法

计算属性权重的步骤为：

步骤2 利用定义7规范化加权评价表[ωPlqlij]HMN;

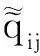
步骤5 采用文献[13]中的规范化方法,将相离度矩阵[di j]M ×N规范化为[ui j]M ×N, 显然有

3 决策方法

其中:

步骤3 确定属性的正负有效综合理想属性值，如下：

步骤4 根据定义3, 将每个方案的成本型或效益型的综合有效评价值与正负有效综合理想属性值进行测度,以此求出每个方案的有效综合属性的测度结果T(Ai)：

T(Ai)=T(Ai(J1))+T(Ai(J2)),i∈{1,2,…，M}.

(1)

4 数值算例

某企业为了开展校企合作项目,聘请了4位投资专家从投资金额(G1)、可能利润(G2)、风险盈利值(G3)、可能损失值(G4)等4个维度对5所学校的投资环境进行综合评估.评估结果以区间数据信息形式给出,其中G1和G4为成本型属性,G2和G3为效益型属性.专家评分表见表1(单位为百万元).

表1 专家评分表

4.1 计算投资专家权重

表2 测度表

4.2 确定属性权重

第4步 求解熵值Sj及属性权重ωGj.经计算, 熵值Sj和权重ωGj分别为:S1= 0.621 7,S2=0.811 0,S3=0.730 2,S4=0.818 2,ωG1=0.371 3,ωG2=0.185 5,ωG3=0.264 8,ωG4=0.178 4.

4.3 决策方法

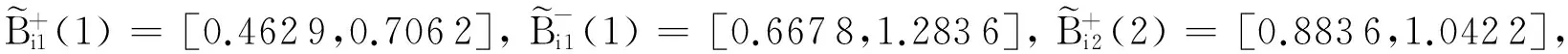
根据式(1)计算所得的各方案的有效综合属性测度结果T(Ai)(i=1,2,3,4,5)见表3.由表3可得T(A1)= 9.981 8,T(A2)=12.893,T(A3)=10.556 8,T(A4)=5.949 8,T(A5)=9.598 8, 由此知各学校综合投资环境的排序为A2≻A3≻A1≻A5≻A4.

表3 各方案的有效综合属性测度结果

4.3.2为了检验本文决策方法的有效性,采用文献[12]中的决策方法与本文的决策方法进行对比.根据定义5,文献[12]中的决策方法的步骤为:

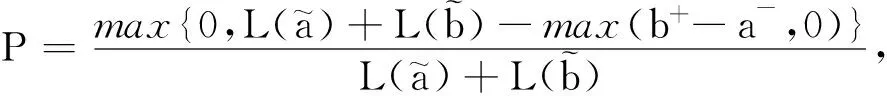
5 结束语

本文建立了一种求解评价专家权重和属性权重的简洁模型,并利用区间数的积型贴近度公式提出了一种区间数的多属性群决策方法.实例验证表明,本文提出的区间数多属性群决策方法能够充分利用评价专家给出的决策信息,具有简单、直观、便于计算等优点.由于本文研究的只是属性信息为区间数的情形,因此在实际决策问题中,决策者可根据不同类型和属性的信息进行多元化的分析,以此建立更加科学、合理的多属性群决策方法.