基于Chua电路的一种新型忆阻电路的混沌动力学分析
李浩申, 姜锐函, 徐红梅
(延边大学 工学院,吉林 延吉 133002)
忆阻器是一种表示磁通与电荷关系的电路器件.由于忆阻器具有记忆功能,且体积小、功耗低[1-3],因此其在保密通信、非易失性存储器、电路设计和人工神经网络等领域得到了广泛应用[4-7].近年来,一些学者将忆阻器应用到混沌电路设计中.例如:吴淑花等利用两个荷控忆阻器模型设计了一个最简五阶混沌电路,并利用常规动力学分析方法研究了该电路的基本动力学特性[8].王振等提出了一种基于双忆阻器的文氏桥混沌电路,研究显示该电路的稳定性与非零特征根和零特征根密切相关[9].陈菊芳等利用RC单T选频网络设计了一种并联型忆阻混沌电路和一种串联型忆阻混沌电路,并分析了其动力学行为[10].基于上述研究,本文构建了一种新型磁控五阶忆阻混沌电路,并通过理论推导、数值仿真、Lyapunov指数谱、分岔图、相图和Poincaré截面图等分析了该电路的动力学特性.
1 磁控忆阻器五阶混沌电路的设计
本文基于经典的Chua电路,用三次型非线性磁控忆阻器代替Chua电路中的Chua二极管,用电感代替Chua电路中的电阻,并将Chua电路中的电感串联成一个电阻.由此得到的五阶磁控忆阻器的电路如图1所示.图1中各元件对应的5个状态变量分别为i1、i2、v1、v2、W(φ).
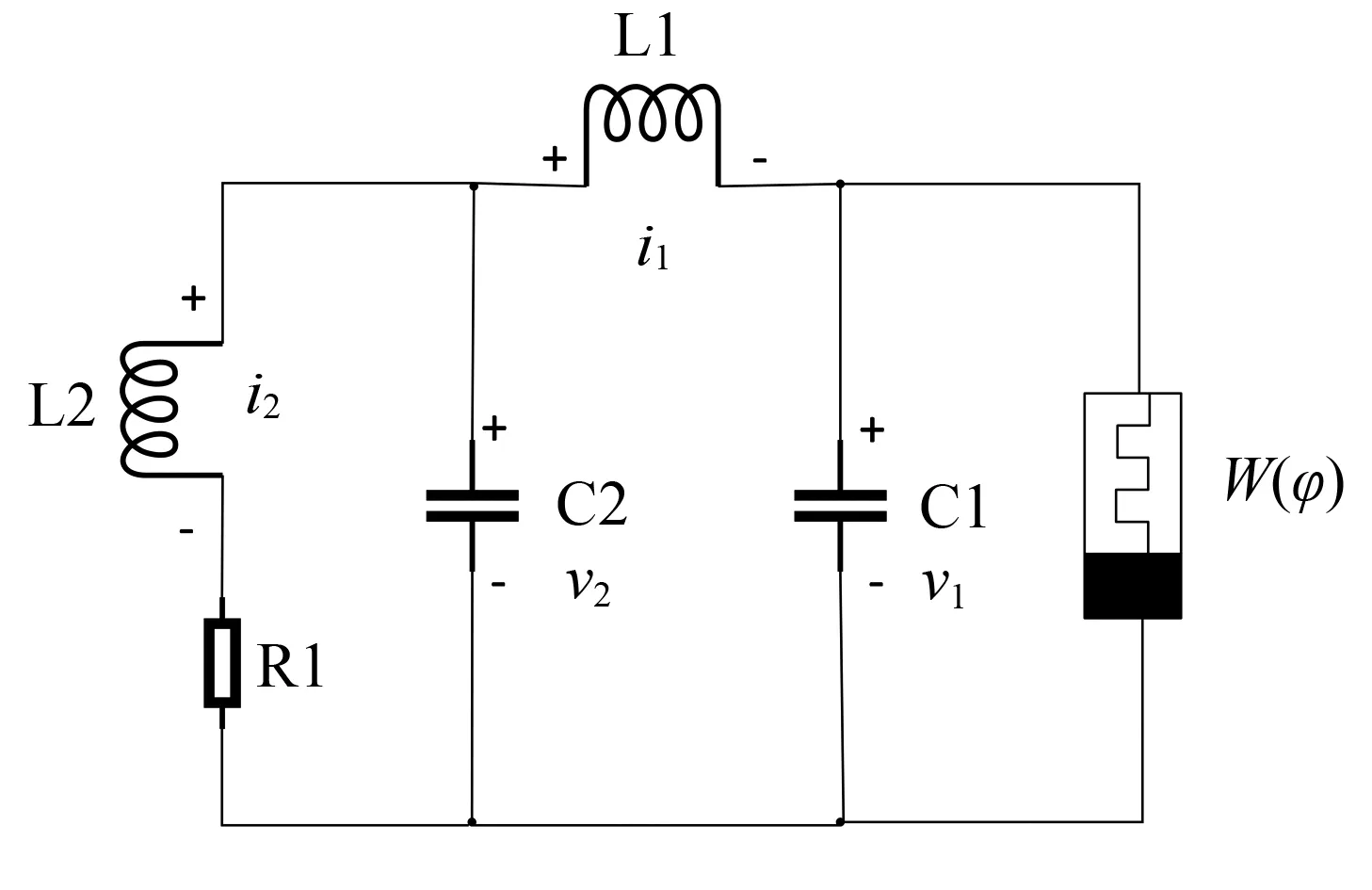
图1 五阶磁控忆阻器的电路图

(1)
其中α和β为常量.
根据基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)以及各元件的伏安特性关系,可得到如下五阶忆阻混沌电路的状态方程:
(2)
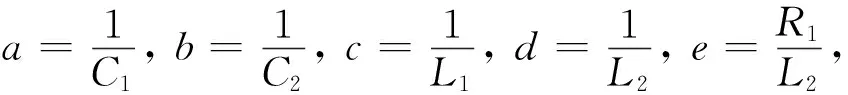
(3)
为了验证系统的动力学特征,本文根据系统的耗散性,采用五阶龙格-库塔离散化算法,电路参数取a=13,b=12,c=9,d=11,e=14,α=-0.7,β=0.3,对初始条件为(0.01,0,0,0,0)的系统(3)进行了仿真,仿真得到的系统的二维相轨迹和三维相轨迹如图2和图3所示.由图2和图3可以看出,各平面相轨图上的混沌吸引子均具有复杂的拉伸和扭曲结构,这表明在上述参数下电路系统处于混沌状态.

图2 二维相轨迹图

图3 三维相轨迹图
图4为不同截面上的庞加莱截面图.由图4可以看到:在x=0截面上,四维Poincaré映射轨线投影在y-z平面上;在u=0截面上,四维Poincaré映射轨线投影在x-y平面上.图5为5个状态变量的时域波形图.由图5可知,5个时域波形图都是非周期性的.

图4 不同截面上的庞加莱截面图

图5 5个状态变量的时域波形图
利用Matlab计算系统的5个Lyapunov指数,得L1=5.244,L2=3.164,L3=0,L4=-16.072,L5=-20.735.利用公式(4)计算系统(3)的Lyapunov维数,得dL=3.63.
(4)
由上述五阶磁控忆阻电路的相轨图、Poincaré映射、时域波形图以及Lyapunov指数和维数可知,该电路系统具有混沌特征[11-14].
2 系统的动力学分析
2.1 系统的耗散性分析
系统(3)的耗散性可由如下公式表示:
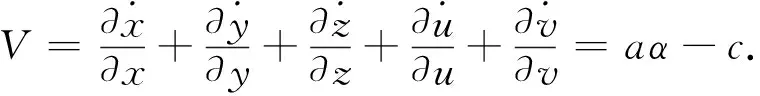
(5)
当参数a=14,α=-0.7,c=9时,公式(5)满足条件aα-c<0.这说明当时间趋近于无穷时,系统(3)的运动轨线总是分布在一个特定的区域内,且具有耗散性.
2.2 系统的平衡点及其稳定性分析
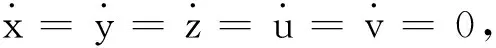
(6)
为得到J在平衡点处的特征方程,令|λE-J|=0, 则集合A的特征方程为:
λ5+[aw(n)+e]λ4+aew(n)λ3=0,
(7)
式中w(n)=α+3βn2.
当参数取a=13,b=12,c=9,d=11,e=14,α=-0.7,β=0.3时,式(7)所对应的特征根方程为:
λ3(λ2+a1λ+a2)=0.
(8)
求解式(8)可得a1=11.7n2+4.9,a2=163.8n2-127.4.再由劳斯稳定判据可知,系统(8)稳定的充分必要条件为:
(9)
式中K=1,2.由式(9)可得:
H1=a1>0,
(10)
H2=a1a0>0.
(11)
再由式(10)和式(11)可得n的稳定范围为:
|n|>0.881 9.
(12)
若忆阻器的初值n在v轴上满足式(12)(其他初值为零),则系统(3)所对应的稳定平衡点集A的解是渐近稳定的,且此时的平衡点集A的特征根实部均为负(除零特征根).若忆阻器的初值n在v轴上不满足式(12),则系统(3)所对应的平衡点集A的解是不稳定的.由以上可知,系统(3)的解是趋于极限环或混沌的.
2.3 系统的Lyapunov指数与分岔图
系统的参数变化不仅会影响系统平衡点的稳定性,同时也会使系统的混沌现象发生改变[15].为了观察和分析系统的混沌动力学的轨迹变化,本文以不同变量的Lyapunov指数和分岔图来分析系统的混沌动力学行为.
改变参数b(b∈[0,20]),其他参数不变(a=14,c=9,d=11,e=14,α=-0.7,β=0.3)时系统的Lyapunov指数和分岔图如图6和图7所示.由图6可以看出,当参数b>7.28时,系统存在大于零的Lyapunov指数,说明此时系统进入混沌状态.由图7可以看出:在0≤b<0.64时,系统出现了一小段混沌状态;在0.64≤b<4.00时,系统的动力学轨迹是一条稳定的直线,表明系统处于极限环的状态;在4.00≤b<7.28时,系统的动力学轨迹开始分岔,系统进入周期态;在7.28≤b<15.96时,系统不再分岔,系统进入混沌状态;在15.96≤b<17.04时,系统的混沌状态逐渐趋于稳定;在17.04≤b<20.00时,系统收敛并再次进入周期态.为了验证系统分岔图的准确性,利用不同参数b所对应的相轨迹图对系统的分岔图进行了验证,结果如图8所示.由图8可以看出,系统的混沌动力学特性在[0,20]区间内呈不同状态.
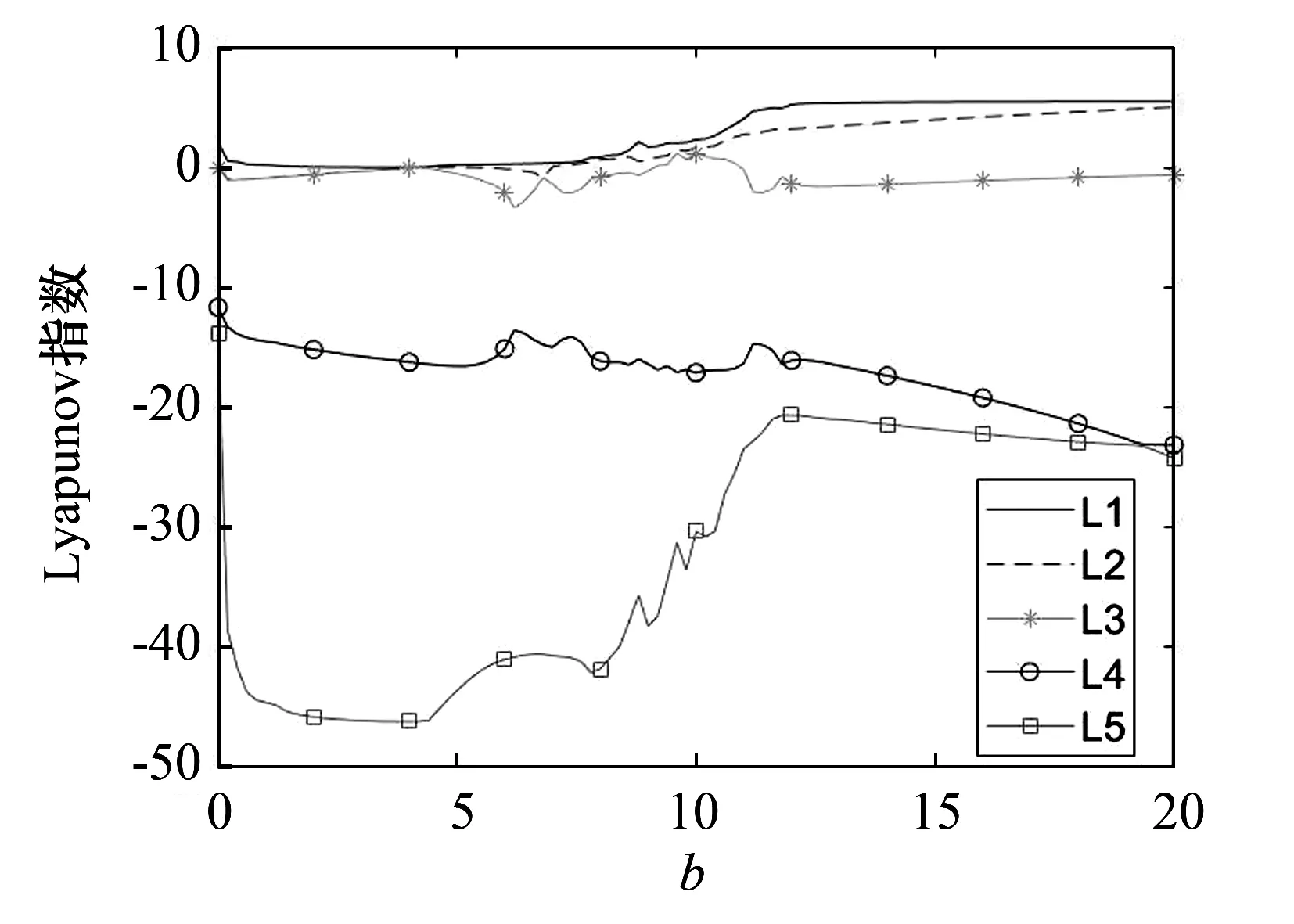
图6 系统Lyapunov指数随参数b的变化情况

图7 系统分岔图随参数b的变化情况
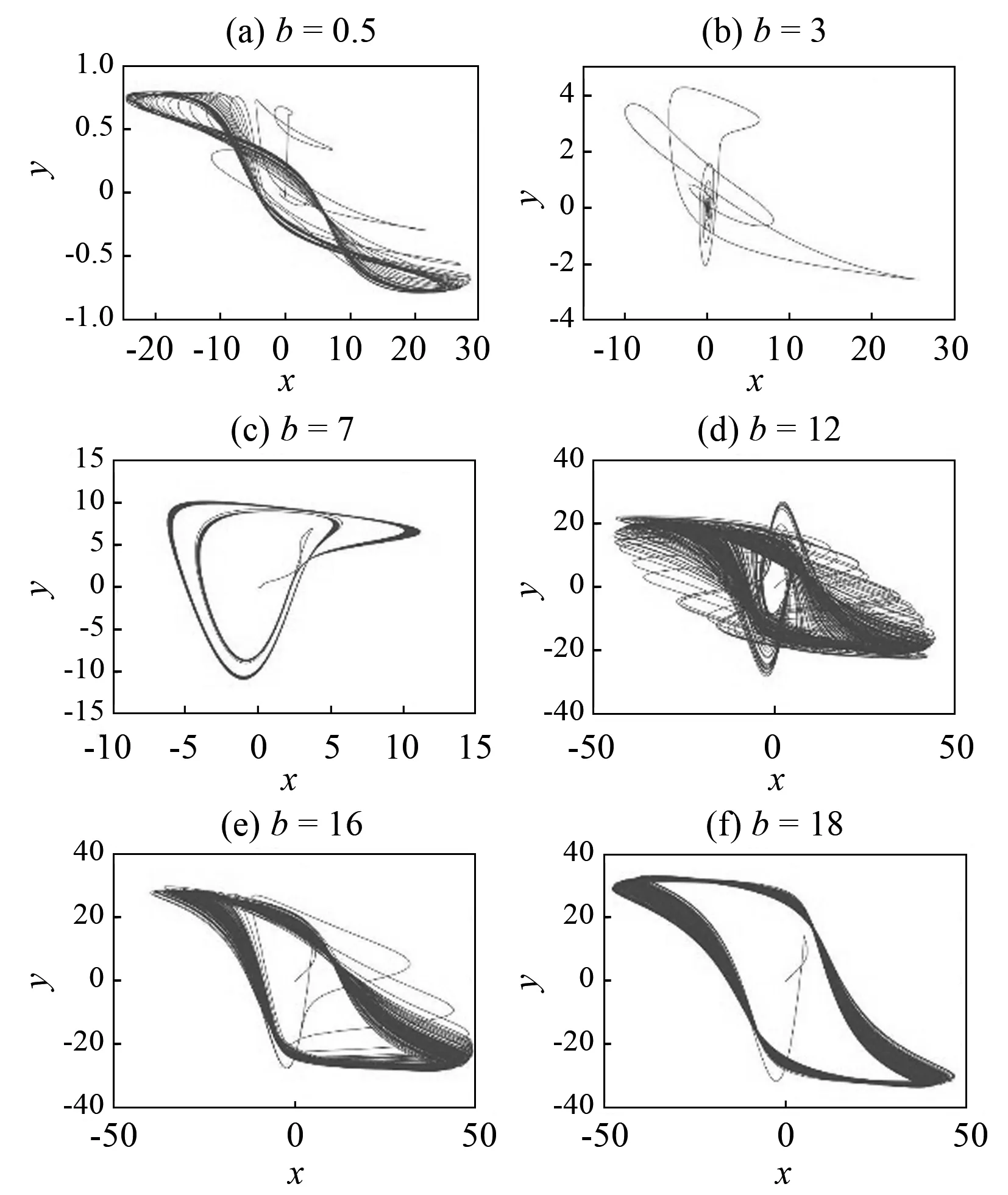
图8 不同参数b所对应的相轨迹
3 忆阻电路的仿真与实现
为了进一步分析忆阻电路的特性,建立了电路系统的Simulink仿真模型,如图9所示.该模型主要由加法器、减法器、乘法器、积分器、增益模块和常数模块组成.忆阻器模型由绝对值模块、乘法器(1—3)、常数(1—2)、加法器1组成,其输出为f+gv2.

图9 电路系统的Simulink建模图





电路系统的Simulink仿真结果如图10所示.与图2对比可以看出,在相同参数和初值下,二者表现出的动力学特性相同,由此表明本文提出的五阶忆阻系统具有混沌特性.
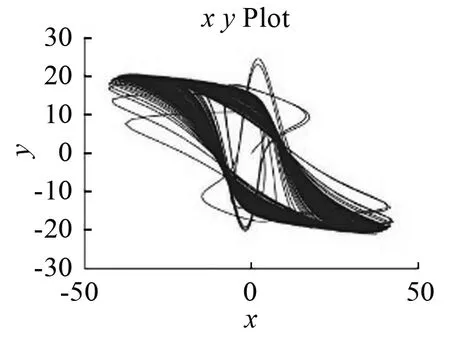
图10 Simulink仿真的相轨迹图
4 结论
基于分岔图、Lyapunov指数、相图、Poincaré截面图和Simulink仿真等方法对本文设计的忆阻电路进行分析表明,本文提出的五阶忆阻电路具有混沌特性,且参数b不同时系统的动力学轨迹表现出不同的运动状态.在今后的研究中,我们将尝试把该忆阻混沌电路应用到存储器和神经网络中,以进一步验证本文方法的可行性.

