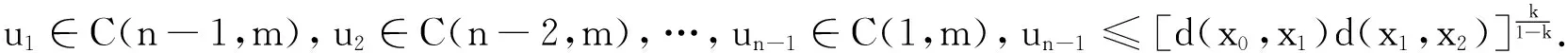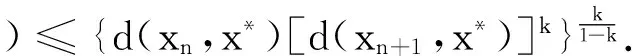乘积度量空间上Β -拟压缩映射的唯一不动点
朴勇杰
(延边大学 理学院,吉林 延吉 133002)
定义1[9]设X是非空集合,称映射d∶X×X→[0,+∞)是X上的乘积度量是指d满足:
(i)对任何x,y∈X,d(x,y)≥1且d(x,y)=1 ⟺x=y;
(ii)对任何x,y∈X,d(x,y)=d(y,x);
(iii)对任何x,y,z∈X,d(x,z)≤d(x,y)d(y,z)(乘积三角不等式).
当d是X上的乘积度量时,称(X,d)为乘积度量空间.
有关乘积度量空间的例子可参看文献[10-12].
定义2[9]设(X,d)是乘积度量空间, {xn}是X中的序列且x∈X.若对任何积性开球Bε(x)={y∈X|d(x,y)<ε},∀ε>1, 存在自然数N且使得n>N时xn∈Bε(x)成立, 则称序列{xn}乘积收敛于x, 并记为xn→x(n→∞).
引理1[10]设(X,d)是乘积度量空间, {xn}是X中的序列且x∈X,则xn→x(n→∞)⟺d(xn,x)→1(n→∞).
定义3[10]设(X,d)是乘积度量空间, {xn}是X中的序列.若对任何ε>1, 存在自然数N且使得n,m>N时d(xn,xm)<ε成立,则称序列{xn}为乘积柯西序列.
引理2[10]设(X,d)是乘积度量空间,{xn}是X中的序列,则{xn}是乘积柯西序列当且仅当d(xn,xm)→1(n,m→∞).
定义4[10]如果乘积度量空间(X,d)中的每个乘积柯西序列都是乘积收敛的,则称(X,d)是完备的.
引理3[10]设(X,d)是乘积度量空间, {xn}和{yn}是X中的两个序列且x,y∈X,则xn→x,yn→y(n→∞)⟹d(xn,yn)→d(x,y)(n→∞).
设(X,d)是完备的乘积度量空间.称T∶X→X是Β-拟压缩映射是指存在k∈[0,1)使得
d(Tx,Ty)≤[v(x,y)]k,∀x,y∈X,
(1)
其中v(x,y)∈A(x,y)∶={d(T2x,x),d(T2x,Tx),d(T2x,y),d(T2x,Ty)}.
定理1设(X,d)是完备的乘积度量空间,T∶X→X是自映射.如果T是Β-拟压缩的,则T有唯一不动点,并且对任何x∈X, 迭代序列{Tnx}收敛于该唯一不动点.
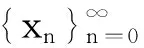
d(xi,xi +1)=d(Txi-1,Txi)≤[v(xi-1,xi)]k,
(2)
其中v(xi-1,xi)∈A(xi-1,xi)={d(T2xi-1,xi-1),d(T2xi-1,Txi-1),d(T2xi-1,xi),d(T2xi-1,Txi)}={d(xi +1,xi-1),d(xi +1,xi),1}.如果v(xi-1,xi)=d(xi +1,xi-1), 则根据式(2)可得d(xi,xi +1)≤[d(xi +1,xi-1)]k; 如果v(xi-1,xi)=d(xi +1,xi), 则根据式(2)可得d(xi,xi +1)≤[d(xi +1,xi)]k, 再根据k∈[0,1)可得d(xi,xi +1)=1≤[d(xi +1,xi-1)]k; 如果v(xi-1,xi)=1, 则根据式(2)可得d(xi,xi +1)=1k≤[d(xi +1,xi-1)]k.综合以上3种情况可得:
d(xi,xi +1)≤[d(xi-1,xi +1)]k,n=1,2,….
(3)
对任何固定的n=1,2,…, 根据式(1)可得:
d(xi,xi +2)=d(Txi-1,Txi +1)≤[v(xi-1,xi +1)]k,
(4)
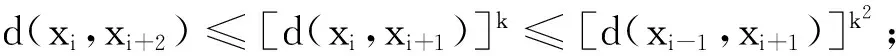
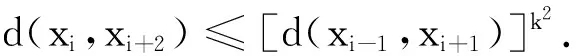
(5)
式(5)可写成如下形式:
(6)
其中k(i,i +2)=k或k(i,i +2)=k2.
以下证明对任何自然数n,当i,j是自然数且满足1≤i,j≤n时,式(7)成立.
(7)
如果n=1, 则i=j=1, 由此显然知式(7)成立.假设n=m时式(7)成立,则可得下式成立:
(8)
设n=m+1.由于在1≤i,j≤m时式(7)和式(8)成立,因此进一步可设j=m+1, 1≤i≤m.由此根据式(1)可得:d(xi,xm +1)=d(Txi-1,Txm)≤[v(xi-1,xm)]k, 其中v(xi-1,xm)∈A(xi-1,xm)={d(xi-1,xi +1),d(xi,xi +1),d(xi +1,xm),d(xi +1,xm +1)}.
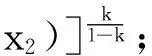
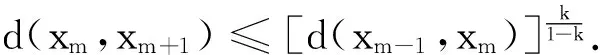
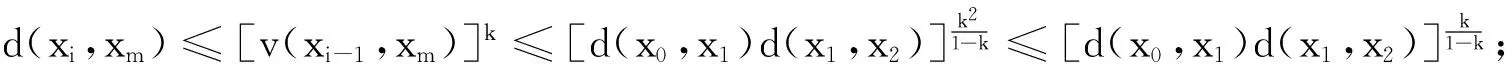
综合上述所有情况并根据归纳原理可知式(7)成立.
对任何m,n∈N且1 (9) (10) 再根据引理2知{xn}是X中的乘积柯西序列,于是根据X的完备性知存在x*∈X使得xn→x*(n→∞).根据定义1中的(iii)和式(1)可知,对任何n∈N有: d(x*,Tx*)≤d(xn,x*)d(Txn-1,Tx*)≤d(xn,x*)[v(xn-1,x*)]k, (11) 其中v(xn-1,x*)∈{d(xn-1,xn +1),d(xn,xn +1),d(xn +1,x*),d(xn +1,Tx*)}. 当v(xn-1,x*)=d(xn-1,xn +1)时,根据式(11)可得: d(x*,Tx*)≤d(xn,x*)[d(xn-1,xn +1)]k. (12) 当v(xn-1,x*)=d(xn,xn +1)时,根据式(11)可得: d(x*,Tx*)≤d(xn,x*)[d(xn,xn +1)]k. (13) 当v(xn-1,x*)=d(xn +1,x*)时,根据式(11)可得: d(x*,Tx*)≤d(xn,x*)[d(xn +1,x*)]k. (14) 当v(xn-1,x*)=d(xn +1,Tx*)时,根据式(11)可得: d(x*,Tx*)≤d(xn,x*)[d(xn +1,Tx*)]k≤d(xn,x*)[d(xn +1,x*)d(x*,Tx*)]k. 整理上式可得: (15) 综合上述4种情况并根据引理1和引理2及k∈[0,1)可知,当式(12)—(15)的两边取n→∞时可得d(x*,Tx*)=1, 这说明x*是T的一个不动点.如果y*也是T的不动点,则根据式(1)可得:d(x*,y*)=d(Tx*,Ty*)≤[v(x*,y*)]k, 其中v(x*,y*)∈{1,d(x*,y*)}.由此容易得到d(x*,y*)=1, 因此x*是T的唯一不动点.再根据xn=Txn-1=Tnx及xn→x*可知,{Tnx}收敛于T的唯一不动点x*. 例1在R=(-∞,+∞)上定义d(x,y)=e|x-y|,∀x,y∈R, 则(R,d)是乘积度量空间.令X={0,1,2}, 则显然可知(X,d)是完备的乘积度量空间.定义f∶X→X,f0=f1=0,f2=1,并取k∈(0.5,1),由此显然有:当x,y∈{0,1}或x=y=2时,d(fx,fy)=1≤[max{d(f2x,x),d(f2x,fx),d(f2x,y),d(f2x,fy)}]k成立;当x=0,y=2时,d(f0,f2)=e|f0-f2|≤e2k≤[max{d(f20,0),d(f20,f0),d(f20,2),d(f20,f2)}]k成立;当x=1,y=2时,d(f1,f2)=e|f1-f2|≤e2k≤[max{d(f21,1),d(f21,f1),d(f21,2),d(f21,f2)}]k成立.由以上计算结果可知,f和k满足定理1的所有条件,因此f具有唯一不动点0.