一类Hadamard型分数阶微分方程解的存在唯一性

甘亦苗， 侯成敏

(延边大学 理学院，吉林 延吉 133002)

0 引言

分数阶微积分方程在许多自然科学领域有着广泛的应用.近年来，一些学者研究了带有边值问题微分方程正解的存在唯一性，并取得了较好的研究成果[1-5].本文研究如下一类Hadamard型具有导数项的分数阶微分方程正解的存在唯一性：

(1)

1 相关知识和引理

定义1[1]函数g∶[1,+∞)→R+,g∈L1[1,+∞)的Hadamard型α∈R+阶分数阶积分为

(2)

定义2[1]函数g∶[1,+∞)→R+的α∈R+阶的Hadamard型分数阶导数为

(3)

引理1[1]若β-1>γ≥0,t>a>1，则有

(4)

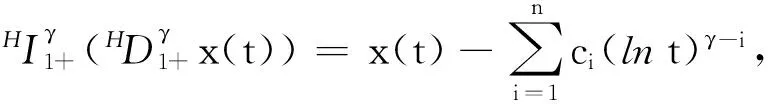
引理3设h(t)∈C[1,∞), 则边值问题

(5)

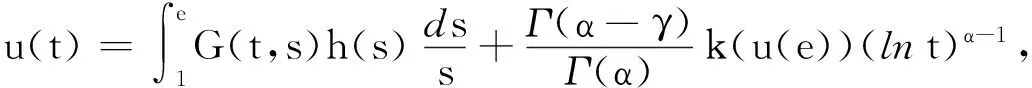
(6)

(7)

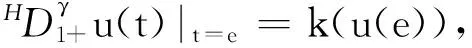
引理4[6]由式(6)定义的格林函数具有如下性质：

1)G(t,s)∶[1,e]×[1,e]→[0,∞)是连续的；

2)∀t,s∈[1,e]，有:

0≤(lnt)α-1(1-lns)α-γ-1[1-(1-lns)γ]≤Γ(α)G(t,s)≤(lnt)α-1(1-lns)α-γ-1,

(8)

0≤(lnt)α-β-1(1-lns)α-γ-1[1-(1-lns)γ]≤HDβ1+Γ(α-β)G(t,s)≤

(lnt)α-β-1(1-lns)α-γ-1.

(9)

引理5[1]设P是一个正规锥，A,B∶P×P→P是两个混合单调算子，且C∶P→P是一个减算子.假设以下条件成立：

(A1)∀t∈(0,1)，存在φ(t)∈(0,1]，使得A(tx,t-1y)≥φ(t)A(x,y),∀(x,y)∈P；

(A2)∀t∈(0,1)，有B(tx,t-1y)≥tB(x,y),∀x,y∈P；

(A3)∀t∈(0,1)，有C(t-1y)≥tC(y),∀y∈P；

(A4)∃h>θ且h∈Ph，使得A(h,h)∈Ph,B(h,h)∈Ph,C(h)∈Ph；

(A5)∃δ>0，使得∀x,y∈P，有A(x,y)≥δ(B(x,y)+C(y)).

根据以上假设有:

(1)A∶Ph×Ph→Ph，B∶Ph×Ph→Ph，C∶Ph→Ph；

(2)∃u0,v0∈Ph，且存在r∈(0,1)，使得rv0≤u0≤v0,u0=A(u0,v0)+B(u0,v0)+C(v0)≤A(v0,u0)+B(v0,u0)+C(u0)≤v0;

(3)A(x,x)+B(x,x)+C(x)=x有唯一的解x*∈Ph;

(4)∀x0,y0∈Ph, 依次构造如下序列：

xn=A(xn-1,yn-1)+B(xn-1,yn-1)+C(yn-1),n=1,2,…;

yn=A(yn-1,xn-1)+B(yn-1,xn-1)+C(xn-1),n=1,2,…,

则有xn→x*,yn→y*(n→∞).

2 主要结果及其证明

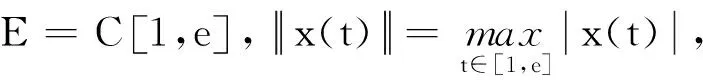
(10)

其中G(t,s)与式(6)相同.

定理1假设以下条件成立：

(H1)f(t,x,y),g(t,x,y)∶[1,e]×R+×R+→R+均为连续函数，且关于第2个变量都是单调递增的，关于第3个变量都是单调递减的.k(y)∶R+→R+为连续的单调递减函数，N∶R+→R+为减算子.

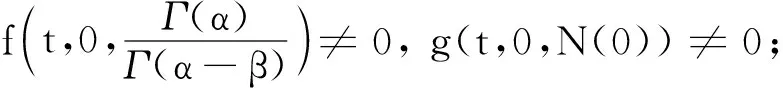
(H3)∃γ∈(0，1)，使得∀t∈(1,e),λ∈(0,1)，有f(t,λx,λ-1y)≥λγf(t,x,y),g(t,λx,λ-1y)≥λg(t,x,y),k(λ-1y)≥λk(y),N(λu)≥λN(u).

(H4)∀t∈(1,e),x∈R+,y∈R+, 存在常数δ1,δ2>0, 有f(t,x,y)≥δ1g(t,x,0)，f(t,x,y)≥δ2k(y).

(H5)p(t),q(t)∶(1,e)→[0,∞)为连续函数，且p(t)≥q(t)≥m>0，其中m∈R+.

则问题(1)有唯一的解u*∈Ph,h(t)=(lnt)α-1.设初始值u0,v0∈Ph，构造两组迭代序列，且un→u*,vn→v*(n→∞)，其中：

证明定义以下算子：

(11)

(12)

(13)

T(u,v)=A(u,v)+B(u,v)+Cv.

(14)

为了方便证明，本文令u(t)u,v(t)v,(u,v)(t)(u,v).由式(9)可得到以下式子:

(15)

(16)

(17)

首先证明A和B是混合单调算子，C是减算子.实际上，对于u1u2,v1v2，有由此根据条件(H1)以及引理4易得：

即A(u1,v2)A(u2,v1)，故算子A是混合单调算子.同理可证B是混合单调算子，C是减算子.

由(H3)有A(λu,λ-1v)≥λγA(u,v),B(λu,λ-1v)≥λB(u,v),C(λ-1v)≥λC(v)，因此算子A、B、C满足引理5的条件(A1)—(A3).

令h=(lnt)α-1,t∈(1,e)，则∀u,v∈Ph存在μ≥1，使得μ-1h≤x,y≤μh.结合引理3和f的单调性可证得:

令:

因为0

令：

最后证明算子A、B、C满足引理5中的条件(A5).根据条件(H4)可得：

因此有A(u,v)δ1B(u,v).再根据条件(H3)和(H4)以及引理4可得：

综上，由引理5可知，算子T存在一个不动点u∈Ph，满足T(u,u)=A(u,u)+B(u,u)+Cu=u，因此问题(1)有唯一的解u∈Ph,h=(lnt)α-1,t∈(1,e).设初始值u0,v0∈Ph，构造两组迭代序列{un}和{vn}，t∈(1,e)：

根据引理5可知，存在(u*，v*), 满足un→u*,vn→v*(n→∞)，且u*,v*∈Ph.