考虑接触刚度的周向拉杆转子–轴承系统动力学特性分析

崔颖，张晗，黄宇熙

考虑接触刚度的周向拉杆转子–轴承系统动力学特性分析

崔颖，张晗，黄宇熙

（大连海事大学船舶与海洋工程学院，辽宁省 大连市 116026）

为了探究周向拉杆转子–轴承系统的动力学特性，利用自相关函数法建立三维高斯随机粗糙表面数值模型，并通过Ansys APDL生成粗糙表面几何模型。利用Abaqus软件对粗糙表面进行有限元接触仿真计算，得到不同预紧力下单位面积粗糙表面的接触刚度，进而建立了考虑接触刚度的某型燃气轮机周向拉杆转子–轴承系统有限元模型。计算得到了不同预紧力、轴承装配间隙下该系统的动力学特性，结果表明：转子系统的临界转速随预紧力的增大而呈非线性增大趋势；轴承处转子过临界转速时，不平衡响应振幅随预紧力和轴承装配间隙增大而增大。

拉杆转子；接触刚度；轴承装配间隙；动力学特性

0 引言

重型燃气轮机由于其热–功转换效率高，多应用于蒸汽–燃气联合循环发电领域[1-2]。我国目前设计研制的300MW重型燃气轮机转子采用的是拉杆连接，各级轮盘均采用周向多根拉杆连接，使其转子重量轻、冷却性能好，但是与连续转子相比，拉杆转子具有多个接触结合面，拉杆预紧力、结合面粗糙度等因素都会对拉杆转子的动力学性能产生影响。结合面的接触特性以及考虑结合面接触刚度的拉杆转子动力学特性，是拉杆转子研究中的重点。

与连续性转子相比，拉杆转子最大的特点是轮盘间的接触作用，在拉杆转子动力学特性的研究中，轮盘间接触刚度的计算十分重要。针对接触刚度与其各影响因素之间的非线性关系，国内外学者进行了大量的研究。Greenwood等[3]基于Hertz模型提出了基于统计学的经典GW接触模型，学者们在GW模型的基础上进行了大量修正，如： Whitehouse等[4]提出了引入联合概率密度函数来描述粗糙峰高度和曲率半径关系的WA模型；赵永武等[5-7]提出了考虑发生塑性变形与微凸体之间相互作用的ZMC模型；Majumdar等[8]基于W-M分形函数提出了M-B分形接触模型。学者们基于特定的接触面假设模型，分析得到接触刚度，再通过有限元法、集总参数法[9]、键合图法[10]等研究拉杆转子的振动特性。李忠刚等[11]研究了分布式拉杆转子系统扭转振动的非线性动力学特性。胡亮等[12-14]针对转轴裂纹、动静碰磨以及各拉杆螺栓预紧力分布不均匀等因素对拉杆转子动力学特性的影响进行了研究。吴进军等[15]对预紧力与粗糙度对拉杆弯曲振动特性的影响进行了研究。随着有限元法技术的发展，利用有限元软件仿真计算得到粗糙表面的接触刚度，能够使得接触刚度的预测精度进一步提高。因此，通过开展粗糙表面有限元接触分析得到接触刚度，进而分析预紧力对周向拉杆转子–轴承系统的动力学特性的影响，对于燃气轮机轴系动力学设计具有理论和工程指导意义。

本文首先对周向拉杆转子–轴承系统轮盘间接触面的表面形貌进行了三维几何建模，采用有限元法对粗糙表面与刚性平面进行了弹塑性接触分析，得到了不同预紧力下的法向接触刚度，然后针对某型燃气轮机周向拉杆模型转子–轴承系统，探究了预紧力对周向拉杆转子–轴承系统固有特性的影响，以及预紧力和轴承装配间隙对周向拉杆转子–轴承系统不平衡响应的影响。

1 粗糙表面接触刚度仿真计算

本文采用有限元法进行粗糙表面接触刚 度的计算，首先利用二维数字滤波方法模拟高斯随机表面，基于该表面数据利用APDL命令流生成粗糙表面几何模型，然后进行有限元接触计算分析。

1.1 粗糙表面几何模型构建

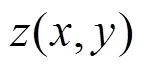
式中：d为均方根粗糙度；tx、ty分别为x、y方向上的相关系数。

本文针对均方根粗糙度=1.0，相关系数=t=15的粗糙表面进行仿真计算，建立尺寸为200mm×200mm的粗糙表面数值模型，如图2所示。

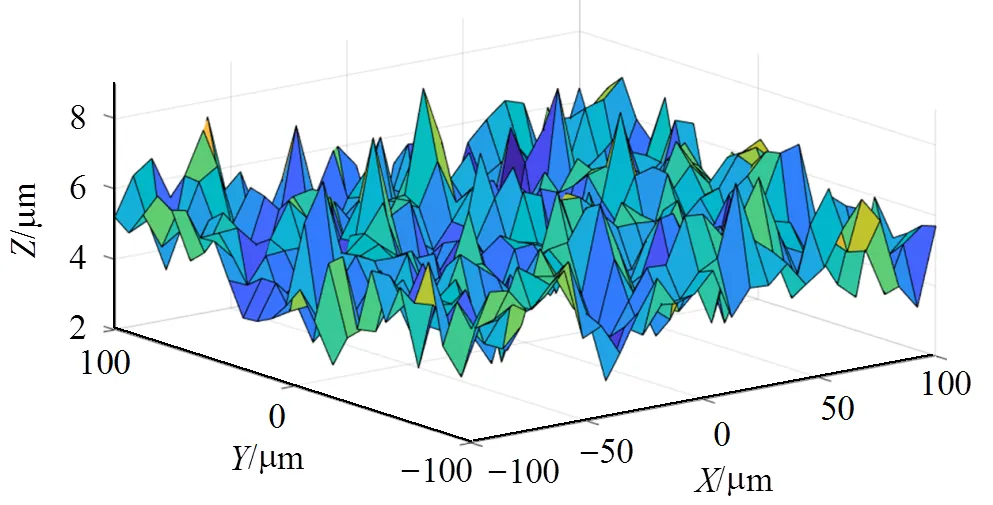
图2 粗糙表面数值表征

为了能够使用有限元软件对粗糙表面进行接触仿真计算，本文采用Ansys APDL命令流进行程序化建模，从而得到如图3所示的粗糙表面几何模型[17]。

图3 粗糙表面几何模型

1.2 粗糙表面接触刚度有限元仿真计算

利用有限元法进行粗糙表面接触刚度计算，采用Abaqus软件进行接触力学分析，建立如图4所示的刚性平面与粗糙表面接触模型。

图4 有限元接触分析模型

所研究材料为不锈钢，弹性模量为200GPa，泊松比0.28，塑性本构关系设置如表1所示。

表1 材料塑性本构关系参数

Tab.1 Parameters of material plastic constitutive relation

通过仿真计算得到在不同预紧力下单位面积粗糙表面的法向接触刚度，结果如表2所示。在进行转子动力学分析时，需要考虑的是轮盘间的弯曲刚度，弯曲刚度c与法向接触刚度n之间的关系式为

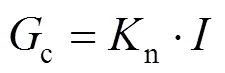
式中为截面惯性矩。

表2 不同预紧力下的法向接触刚度

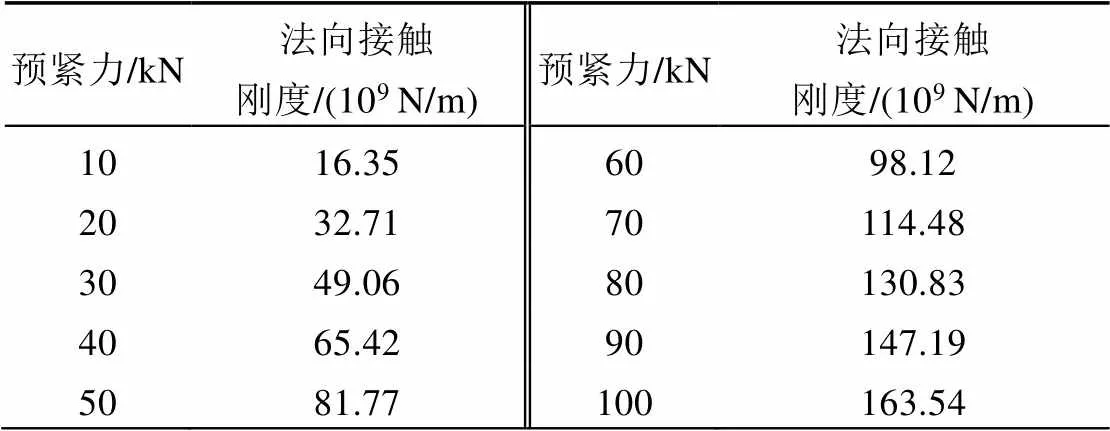
Tab.2 Normal contact stiffness under different preloads

2 考虑接触刚度的周向拉杆转子–轴承系统动力学建模

本文采用如图5所示的周向拉杆转子，该转子8级压气机盘和2级涡轮盘分别采用8根拉杆周向连接，各级轮盘间接触面均方根粗糙度=1.0，该模型转子的总长度为1.065m，总质量为69.5kg。

图5 周向拉杆转子三维实体模型

周向拉杆转子系统采用如图6所示的四瓦可倾瓦轴承，轴承刚度为K=K=1.91´108N/m，轴承阻尼为D=D=34.47N·s/m。

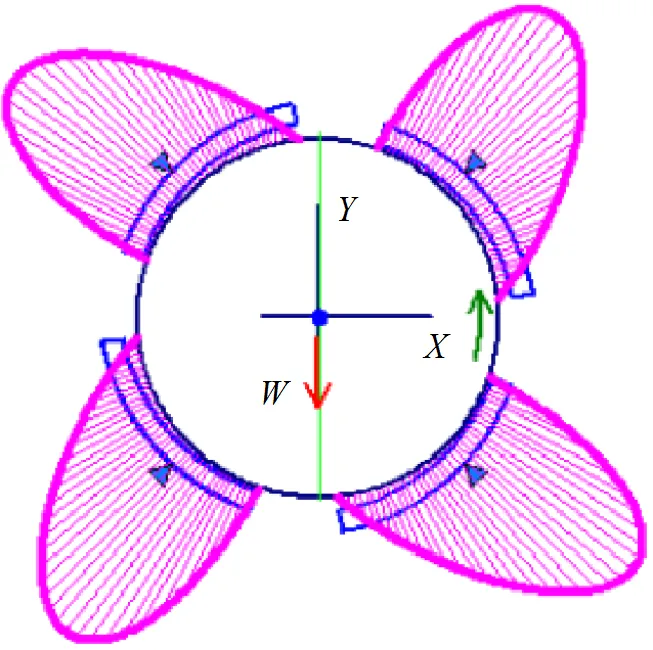
图6 四瓦可倾轴承示意图

对周向拉杆转子–轴承系统模型进行单元划分。压气机端轴承(1#轴承)和涡轮端轴承(2#轴承)分别位于5#和61#节点处，周向拉杆转子–轴承系统有限元模型如图7所示。

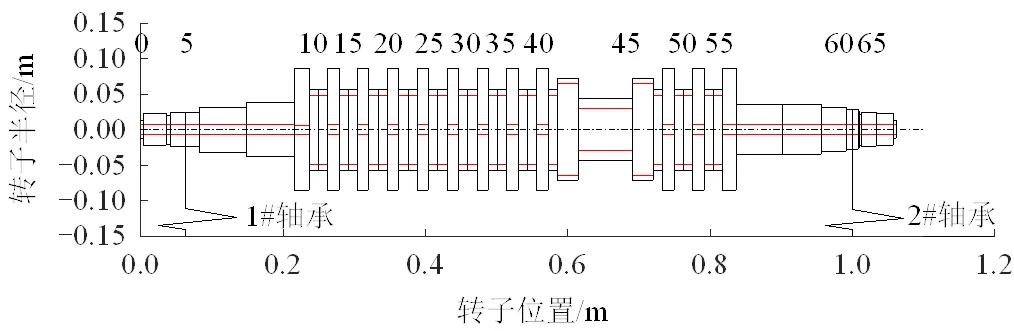
图7 周向拉杆转子–轴承系统有限元模型

采用Timoshenko梁单元，考虑梁的转动惯量、剪切变形和陀螺效应，周向拉杆转子–轴承系统运动微分方程为

3 周向拉杆转子–轴承系统固有特性分析

基于周向拉杆转子–轴承系统动力学方程，得到不同预紧力下周向拉杆转子–轴承系统的前3阶正进动临界转速，如图8所示。

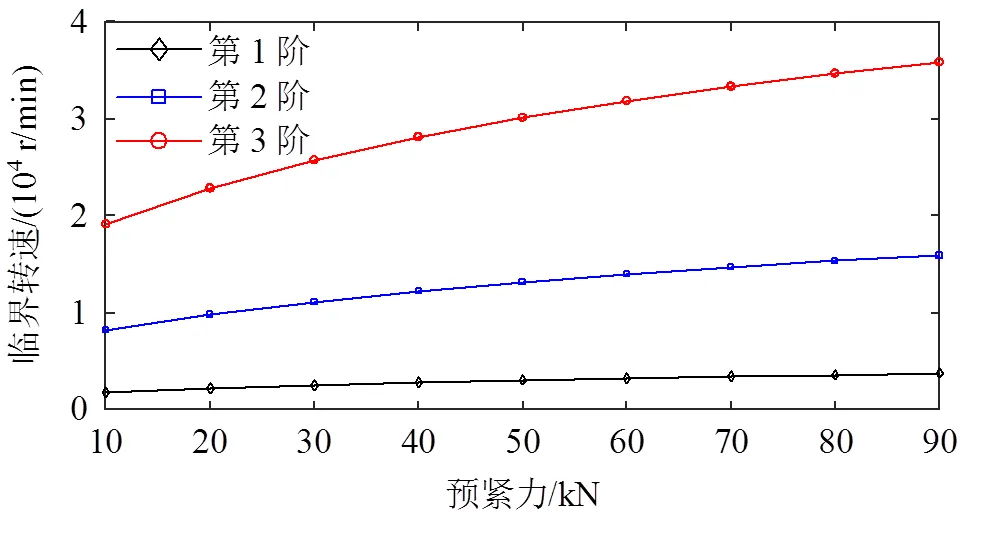
图8 临界转速随预紧力变化规律

由图8可知，随着预紧力增大，周向拉杆转子–轴承系统前3阶临界转速呈现非线性增加的趋势。

周向拉杆转子–轴承系统各阶振型随预紧力变化并不显著，预紧力50kN时前3阶振型如 图9所示。

图9 预紧力为50kN时拉杆转子–轴承系统振型

4 周向拉杆转子–轴承系统动力学响应分析

4.1 预紧力对周向拉杆转子–轴承系统动力学响应的影响

设压气机第1个轮盘处(8#节点)有225kg·mm不平衡量，分别选取拉杆预紧力为10、20、30kN，采用Newmark数值积分法计算得到转子在2个轴承处(5#、61#节点)，以及8#节点处不平衡响应如图10所示。

由图10可以看出，随着预紧力增大，周向拉杆转子–轴承系统的临界转速也随之增大，在轴承处，转子过临界转速时的不平衡响应振幅也随之增大；而在存在不平衡量的轮盘处(8#节点)，过第1阶临界转速时的不平衡响应振幅随之先减小后增大，过第2阶临界转速时振幅随之降低。

4.2 轴承装配间隙对周向拉杆转子–轴承系统动力学响应的影响

不同的轴承装配间隙下轴承的刚度、阻尼也不同，装配间隙分别为50、60、70mm时，轴承的刚度、阻尼如表3所示。

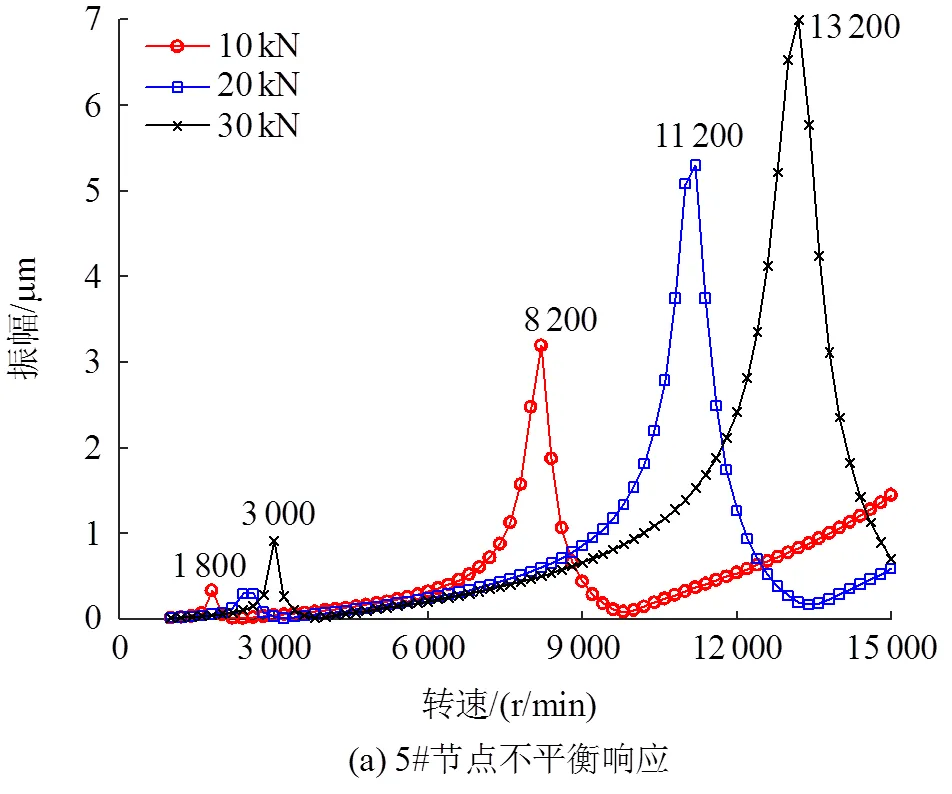
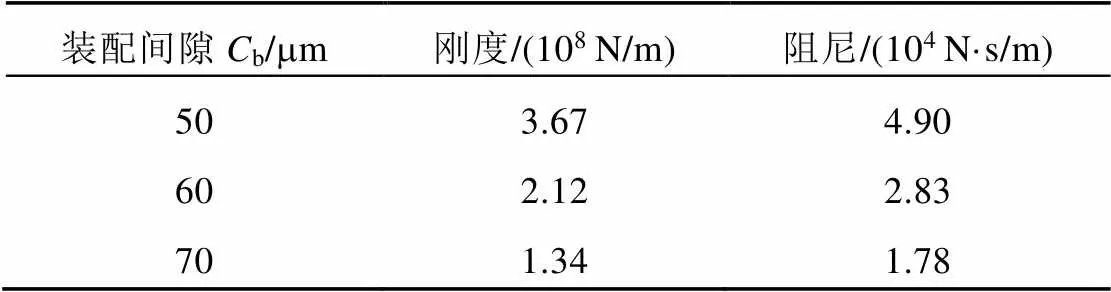
表3 不同装配间隙下的轴承动力学参数

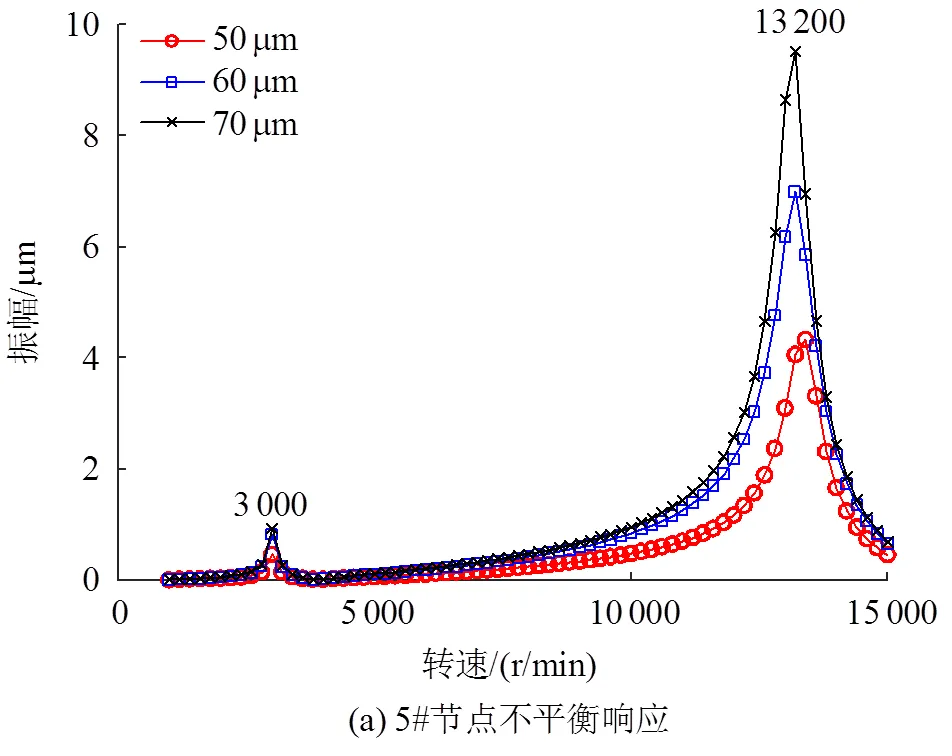
在拉杆预紧力为30 kN情况下，设压气机第一个轮盘处(8#节点)有225kg·mm不平衡量，分别计算得到轴承间隙为50、60、70mm时拉杆转子在2个轴承处(5#、61#节点)，以及8#节点的不平衡响应如图11所示。

由图11可以看出，随着轴承装配间隙增大，由于轴承刚度降低，周向拉杆转子–轴承系统的前2阶临界转速也有所降低。在2个轴承处，过临界转速时的不平衡响应振幅随之增大；而在存在不平衡量的轮盘处(8#节点)，过第1阶临界转速的不平衡响应振幅几乎没有变化，过第2阶临界转速时的不平衡响应振幅则是先减小后增大。

5 结论

1）在粗糙表面三维数值建模的基础上，通过Abaqus对粗糙表面进行有限元仿真计算，得到不同预紧力下粗糙表面的接触刚度，能够有效提高周向拉杆转子–轴承系统动力学模型的精度。

2）随着预紧力增大，周向拉杆转子–轴承系统前3阶临界转速呈非线性增加趋势；在2个轴承处，转子过临界转速时的不平衡响应振幅也随之增大；而在存在不平衡量的轮盘处，过第1阶临界转速时不平衡响应振幅随之先减小后增大，过第2阶临界转速时振幅随之降低。

3）随着轴承装配间隙增大，由于轴承刚度降低，周向拉杆转子–轴承系统的前2阶临界转速也有所降低。在2个轴承处，过临界转速时不平衡响应振幅随之增大。存在不平衡量的轮盘处，过第1阶临界转速的不平衡响应振幅几乎没有变化，过第2阶临界转速时的不平衡响应振幅则是先减小后增大。

[1] 方继辉，王荣．重型F级燃气轮机IGV开度对压气机效率的影响[J]．发电技术，2020，41(3)：317-319．

FANG J H，WANG R．Influence of IGV opening degree on the compressor efficiency of MITSUBISHI F4 gas turbine[J]．Power Generation Technology，2020，41(3)：317-319．

[2] 刘石，蔡笋，邓小文，等．基于CRN方法的重型燃气轮机燃烧室排放研究[J]．广东电力，2019，32(3)：37-44．

LIU S，CAI S，DENG X W，et al．Study on emission of heavy duty gas turbine combustor based on CRN approach [J]．Guangdong Electric Power，，2019，32(3)：37-44．

[3] GREENWOOD J A，WILLIAMSON J B P． Contact of nominally flat surfaces[J]．Proceedings of the Royal Society of London，1966，295(1442)：300-319．

[4] WHITEHOUSE D J， ARCHARD J F．The properties of random surfaces of significance in their contact [J]．Proceedings of the Royal Society of London，1971，316(1524)：97-121．

[5] ZHAO Y W，MAIETTA D M，CHANG L．An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow[J]．Journal of Tribology，2000，122(1)：86-93．

[6] ZHAO Y W，CHANG L．A model of asperity interactions in elastic-plastic contact of rough surfaces[J]. Journal of Tribology，2001，123(4)：857-864．

[7] 赵永武，吕彦明，蒋建忠．新的粗糙表面弹塑性接触模型[J]．机械工程学报，2007，43(3)：95-101．

ZHAO Y W，LÜ Y M，JIANG J Z．New elastic-plastic model for the contact of rough surfaces[J]．Journal of Mechanical Engineering，2007，43(3)：95-101．

[8] MAJUMDAR A，BHUSHAN B．Fractal model of elastic-plastic contact between rough surfaces [J]．Journal of Tribology，1991，113(1)：1-11．

[9] 卢明剑，孙岩桦，周健，等．拉杆组合转子的刚度修正及动力学建模[J]．航空动力学报，2016，31(9)：2203-2209．

LU M J，SUN Y H，ZHOU J Z，et al．Stiffness modification and dynamic modeling of a rod fastening rotor[J]．Journal of Aerospace Power，2016，31(9)：2203-2209．

[10] 王艾伦，骆舟．拉杆转子扭转振动研究[J]．振动与冲击，2009，28(5)：165-168．

WANG A L，LUO Z．Study on rod fastening rotor’s torsional vibration[J]．Journal of Vibration and Shock，2009，28(5)：165-168．

[11] 李忠刚，陈照波，焦映厚，等．分布式拉杆转子扭转振动系统动力学特性分析[J]．动力学与控制学报，2016，14(2)：143-146．

LI Z G，CHEN Z B，JIAO Y H，et al．Analysis of characteristics of the torsional vibration of the distributed rod fastening rotor system[J]．Journal of Dynamics and Control，2016，14(2)：143-146．

[12] 胡亮，柳亦兵，赵立，等．碰摩拉杆转子非线性动力学响应特性[J]．动力工程学报，2017，37(7)：533-539．

HU L，LIU Y B，ZHAO L，et al．Nonlinear dynamic response characteristics of a rod fastening rotor with rub-impact faults[J]．Chinese Journal of Power Engineering，2017，37(7)：533-539．

[13] 胡亮，柳亦兵，徐晓星，等．带横向裂纹的拉杆转子非线性动力学特性研究[J]．噪声与振动控制，2016，36(5)：11-14．

HU L，LIU Y B，XU X X，et al．Nonlinear dynamic response of a rod fastening rotor with a transverse crack[J]．Noise and Vibration Control，2016，36(5)：11-14．

[14] HU L，LIU Y，ZHAO L，et al．Nonlinear dynamic response of a rub-impact rod fastening rotor considering nonlinear contact characteristic[J]．Archive of Applied Mechanics，2016，86(11)：1869-1886．

[15] 吴进军，陈强．预紧力与粗糙度对拉杆弯曲振动特性影响的研究[J]．振动与冲击，2020，39(9)：63-70．

WU J J，CHEN Q．Lateral vibration characteristics of a rod-fastening rotor considering the tightening force and roughness[J]．Journal of Vibration and Shock，2020，39(9)：63-70．

[16] 陈辉，陈海波，胡元中，等．三维粗糙表面的计算机生成及其纹理控制[J]．润滑与密封，2007，32(8)：42-45．

CHEN H，CHEN H B，HU Y Z，et al．The generation of three dimensional rough surface and the control of texture feature[J]．Lubrication Engineering，2007，32(8)：42-45．

[17] 崔颖，孙唯一，于颖嘉，等．基于正交实验的粗糙表面接触密封性能预测方法[J] ．大连海事大学学报，2019，45(3)：53-58．

CUI Y，SUN W Y，YU Y J，et al．Prediction method of contact sealing performance of rough surface based on orthogonal experiments[J]．Journal of Dalian Maritime University，2019，45(3)：53-58．

Dynamic Characteristics Analysis of Circumferential Rod Fastening Rotor-Bearing System Considering Contact Stiffness

CUI Ying, ZHANG Han, HUANG Yuxi

(College of Naval Architecture and Ocean Engineering, Dalian Maritime University, Dalian 116026, Liaoning Province, China)

In order to explore the dynamic characte-ristics of the circumferentialrod fastening rotor-bearing system, a numerical model of three-dimensional Gaussian random rough surface was established by using the method of autocorrelation function. Moreover, the geometric model of rough surface was generated by Ansys APDL. Abaqus software was used to simulate the contact of rough surface, and the contact stiffness of rough surface under different preloads was obtained. The finite element model of the circumferential rod fastening rotor-bearing system of a certain type of gas turbine considering the contact stiffness was also established. The dynamic characteristics of the system with different preloads and clearances of bearing assembly were calculated. It is shown that critical speed of rotor-bearing system increases nonlinearly with the increase of preload, and the amplitude of unbalance response increases with the increase of preload and clearance of bearing assembly as the rotor has passed the critical speed.

rod fastening rotor; contact stiffness; assembly clearance of bearing; dynamic characteristics

2021-05-07。

10.12096/j.2096-4528.pgt.21052

TK 05

辽宁省自然科学基金指导计划项目(201602070)。

Project Supported by Guiding Plan of Natural Science Foundation of Liaoning Province (201602070).

(责任编辑 辛培裕)