基于Hertz接触理论的法向接触刚度计算方法

关庆华 ，赵 鑫 ，温泽峰 ，金学松

（西南交通大学牵引动力国家重点实验室，四川 成都 610031）

车辆-轨道耦合动力学将车辆和轨道系统通过轮轨接触来实现车辆系统和轨道系统的动态相互作用计算，真实地反映了车辆和轨道的动态特性，已广泛应用于铁道车辆和轨道的动力学计算、结构设计及安全评估等[1].其中，轮轨法向力的计算是确定车辆及轨道系统运动和振动的基础，法向力的计算还将影响到接触斑和轮轨蠕滑力的大小，进而将影响整个车辆和轨道系统的动态特性[2-3].

此外，通过有限元模型来分析车辆和轨道系统振动[4]以及计算高频轮轨冲击力[5]和轮轨噪声[6]中，也需要精确的轮轨力确定方法.20 世纪70 年代，英国铁路技术研究所的Jenkins 等[7]在研究车辆和轨道参数对轮轨垂向力的影响时，给出了锥形踏面和磨耗型踏面的轮轨接触常数公式，分别如式（1a）和式（1b）.

式中：Gc和Gw分别为1∶20 锥形踏面和磨耗型踏面的接触常数；参数R与车轮轮径r相等.

该经验公式适用的轮径范围为0.150～0.600 m，对应的钢轨顶面廓形的横向曲率半径为0.230 m.根据式（1a）和式（1b）可确定出接触变形量δ和法向力P之间的关系为

孙翔[8]根据Hertz 弹性体接触理论，针对轮轨接触特定情况，给出了确定轮轨接触椭圆的直接方法，可通过参数ρ/r（ρ为由轮轨主曲率之和确定的常数）直接确定轮轨接触椭圆的各个参数及无量纲蠕滑系数，但未给出弹性接触力及接触刚度的计算方法.

弹性理论及接触力学著作[2,9]中仅给出了Hertz弹性接触斑长、短轴系数的计算公式，关于弹性体Hertz 接触刚度的计算及其数表尚不多见，仅文献[3]中给出了9 组插值数据，不便于工程计算.Hertz 接触理论属于经典的弹性接触力学，在实际的接触过程中材料塑性及阻尼也会对接触力产生影响[9-16].

本文基于Hertz 弹性体接触理论[2-3]，给出了满足Hertz 接触条件的的弹性体接触刚度通用计算公式，并针对轮轨接触特定条件，在文献[8]研究结果的基础上，确定了轮轨接触刚度的简化计算方法和计算数表，以期对车辆-轨道耦合动力学中的轮轨力计算进行修正，并为轮轨摩擦磨损、高频冲击振动和噪声研究中轮轨载荷确定提供计算依据.

1 Hertz 弹性体接触的基本公式

Hertz 接触理论的基本假设如下：

条件1两接触体在初始接触点附近的表面至少二阶连续.故表面在初始接触点的二阶微分邻域内可表示为椭圆抛物面、柱面或双曲抛物面，可以用微分几何的方法进行分析.

条件2接触是非共形的.在加载过程中由初始接触点逐渐形成接触区.由于接触区很小，在初始接触点附近两弹性体可视为弹性半空间.

条件3小变形.在初始接触点附近，两接触表面与初始接触点处公切面法线相交的点相接触.

条件4无面内摩擦，因而切向面力为0.

一般而言，对于非共形轮轨接触，条件1～3 是满足的，但轮轨蠕滑的存在使得条件4 不满足.Johnson[9]指出，两非共形体接触时，只有当其材料弹性常数不同时，摩擦力才会对法向接触产生影响.因此，在目前的动力学分析中，通常认为法向接触力和切向蠕滑力是解耦的，不考虑轮轨蠕滑对法向力的影响.

1.1 计算接触椭圆及载荷变形关系的基本公式

考虑一般性条件，Hertz 接触计算系数A和B可用式（3）、（4）求得.

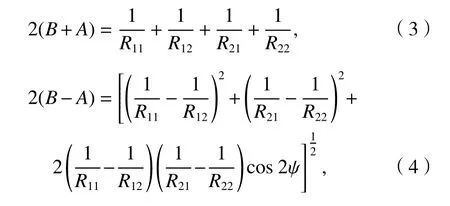
式中：R11、R12和R21、R22分别为接触体1 和接触体2沿接触坐标系纵向、横向的主曲率半径；ψ为两接触体包含R11和R21法平面的夹角.

根据Hertz 弹性体接触理论，系数A和B与接触椭圆偏心率e之间的关系为

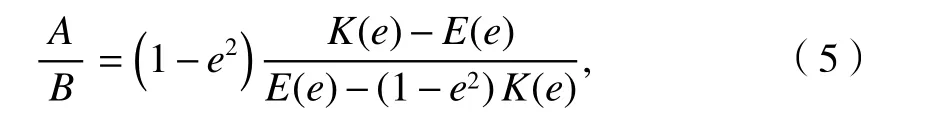
式中：e2=1-（be/ae）2，ae、be分别为接触椭圆长、短半轴长度；K（e）、E（e）分别为以Φ为积分变量的第一、二类完整椭圆积分：

接触点确定后，即可通过接触体主曲率半径及夹角ψ，根据式（3）～（7）计算出接触椭圆的偏心率及其对应的第一、二类完整椭圆积分.

根据接触椭圆偏心率及第一、二类完整椭圆积分可确定出接触椭圆长、短半轴长度分别为

式中：P为法向压力；

其中：νi、Ei分别为接触体i（i=1，2）的泊松比和弹性模量.

弹性接触引起的压缩量与法向力之间的关系为

式中：Knr为Hertz 接触常数，可表示为

若换算为类似于式（1a）和式（1b）的表示方式，为

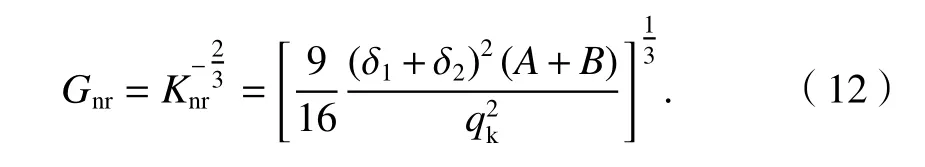
显然，Knr和Gnr与弹性体的材料参数、主曲率半径及其对应的椭圆完整积分有关.

1.2 以ρ/R11 为参数的接触椭圆及载荷与变形计算

在轮轨接触特定条件下，确定轮轨非线性接触常数可进一步简化.

钢轨纵向曲率为0，即1/R21=0，同时忽略ψ后，式（3）和（4）分别为

式中：R11为车轮的法向滚动圆半径，R11=rsecα，α为车轮踏面斜率角；R12为车轮踏面横向曲率半径，圆心指向车轮内部时为正，否则为负；R22为钢轨顶面横向曲率半径，凸形轨头为正.

引入参数ρ：

式（18）给出了ρ/R11和θ的关系，分别对应接触椭圆长轴垂直于轨道纵向和沿轨道纵向的情况.

由式（8）、（9）及式（14），可将ae和be以ρ/R11分别表示为

根据式（5）即可计算接触椭圆的偏心率，对于轮轨接触，可根据式（19）～（22），通过ρ/R11来确定接触椭圆长短轴大小及Hertz 接触常数Knr和Gnr.

为便于计算中查表使用，将θ、A/B、ρ/R11、m、n及qk制作成数表，如附加材料表S1 所示.其中，θ、A/B、m、n及qk为通用参数，适用于任何满足Hertz接触条件的弹性体接触计算，而ρ/R11可用于轮轨接触的查表计算，与文献[8]的插值表格对应，可直接供车辆轨道耦合动力学计算使用.

需要指出的是：式（1a）和式（1b）中R为车轮半径，即R=r，在文献[1,7-8]中均以此计算.由于Hertz接触是以接触体的主曲率半径来计算的，应以车轮的法向滚动圆半径R11来代替，因此，本文的公式和数表均以ρ/R11为参数给出.

2 Hertz 非线性接触刚度

Hertz 接触常数Knr有时也被称为Hertz 非线性刚度，单位为N/m2/3，因此，其并非传统意义的刚度，它依赖于接触体的材料参数、接触点的主曲率半径及两接触体包含R11和R21法平面的夹角，与载荷无关.

Jenkins 等[7]在计算轮轨冲击力P1时，使用了线性化轮轨接触刚度，其定义为

式中：khl与法向力P和静轮载Po有关，需迭代求解.

根据刚度的定义，由式（10）可直接得到Hertz非线性接触刚度为

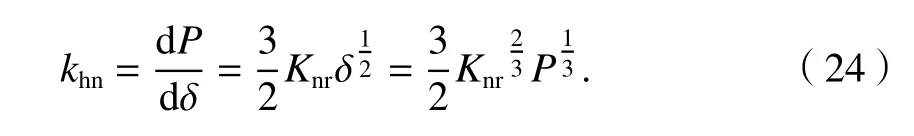
显然，khn不仅由Knr决定，还与P有关.

3 典型轮轨接触分析

3.1 接触参数qk 的计算分析

按照本文公式，计算得到qk与θ的曲线如图1所示.图中数据表明，θ越小，qk越大，对应的接触常数Knr也越大；当θ＞30°时，qk随θ的增大逐渐趋于定值.相比于文献[3]中结果，本文数表中的qk覆盖范围更广，利用本文公式可计算θ为任意值时的接触常数Knr.

图1 qk 与θ 的关系曲线Fig.1 Relationship curve of qk with respect to θ

3.2 典型轮轨接触工况分析

图2（a）所示为LM 车轮踏面及其横截面曲率半径.图2（b）为CN60 钢轨廓形及横截面曲率半径，轨顶圆弧半径为0.300 m，向两侧依次为0.080 m和0.013 m 的圆弧.

图2 车轮和钢轨踏面Fig.2 Profiles of wheel and rail tread

以上述踏面为例，选取某地铁轮轨参数：车轮名义半径为0.365 m，轮缘内侧距为1.353 m，轨距为1.435 m，轨底坡为1∶40，对横移量在-20～20 mm时的Hertz 接触常数进行了计算，结果如图3 所示.

图3 LM 车轮踏面和CN60 钢轨匹配下的接触常数Fig.3 Contact constants for LM wheel profile and CN60 rail profile

由图3 可知，应用本文式（11）和式（12）计算得到的Hertz 接触常数Knr和Gnr相比于采用式（1a）和式（1b）两种踏面计算公式的计算结果在横移量-20～20 mm 内均有较大差异.其中，基于式（1a）计算的Knr相比于本文结果的变化范围为 -25.97%～71.23%，最小相差为0.68%；基于式（1b）计算得到的Knr均高于本文结果，相对变化范围为0.40%～131.42%.基于式（1a）计算得到的Gnr相比于本文结果的变化范围为 -30.13%～22.20%，最小相差0.45%；基于式（1b）计算的Gnr均低于本文结果，相对变化范围为 -42.84%～-0.26%.

以名义接触位置为例，利用式（11）计算的Knr为6.77 × 1010N/m3/2，而通过式（1a）和式（1b）计算得到的Knr分别为8.17 × 1010N/m3/2和11.08 ×1010N/m3/2，相对于式（11）计算结果分别增大了20.77%和63.77%.利用式（12）以及式（1a）和式（1b）计算的Gnr分别为6.02 × 10-8、5.31 × 10-8m/N2/3和4.33 × 10-8m/N2/3，利用式（1a）和式（1b）的Gnr计算结果相对于式（12）计算结果分别减小了11.82%和28.03%.

3.3 轮径对接触常数的影响

为分析轮径对接触常数Knr和Gnr的影响，分别对名义滚动圆位置和轮缘角接触位置进行了计算.

图4 为名义滚动圆附近计算结果，计算中，不考虑接触角的影响，R12=-0.500 m，R22=0.300 m.图中结果表明，名义滚动圆附近，Knr和Gnr精确计算结果与式（1b）计算结果相对接近，Knr的误差范围为0.02%～3.49%，与式（1a）计算结果相差较大，Knr的误差范围为25.94%～27.26%.

图4 名义滚动位置的接触常数Fig.4 Contact constants for nominal contact position

图5 为轮缘角与钢轨R13 圆弧接触时的计算结果，计算中，接触角取为70°，R12=-0.014 m，R22=0.013 m.图中结果表明，轮缘角接触位置，Knr和Gnr精确计算结果与式（1a）和式（1b）的计算结果相差均较大，其中，式（1b）计算Knr结果相对于本文式（11）计算结果的误差范围为17.32%～27.70%，式（1a）的计算误差范围为41.74%～44.89%.

图5 轮缘角位置的接触常数Fig.5 Contact constants for flange corner position

4 结 论

1）基于Hertz 弹性体接触理论，给出了弹性体接触参数的计算方法和接触刚度参数数表，计算公式考虑到接触体主曲率半径、接触斑形状以及材料参数及载荷，计算数表可用于任意满足Hertz 接触条件（如轮轨、轴承、齿轮等）的弹性体接触斑大小和接触刚度的统一计算，填补了目前弹性理论及接触力学中Hertz 接触数表缺乏接触刚度查表参数的不足.本文数表还融合了以ρ/R11为参数的轮轨特定接触条件的接触刚度插值，可为车辆-轨道耦合动力学中轮轨力计算提供修正.

2）目前采用的轮轨接触常数计算公式为近似的经验公式，仅以锥形踏面和磨耗型踏面区分来考虑轮径的影响，限定于特定的轮径范围和钢轨廓形，在实际应用中具有明显不足.以LM 踏面和CN60钢轨的典型匹配为例，当车轮踏面名义中心附近圆弧与轨顶中心圆弧接触时，现有经验公式中的磨耗型踏面公式计算结果与本文计算结果相比误差较小；其它接触位置时，经验公式与本文计算结果误差较大，最大误差超过131%.

3）本文的接触刚度参数计算公式，适用于满足Hertz 接触条件的弹性接触力计算.实际的接触过程涉及复杂的力学问题和非线性因素，材料塑性变形、第三介质、接触能量耗散等都可能会影响到法向接触力.在多体系统的接触力计算中，除Hertz 弹性接触力外，通常还引入阻尼项来考虑接触过程中的能量损耗.此外，接触过程中的塑性变形和黏弹性阻尼特性以及弹性体波动效应等也需要予以考虑.对于高速轮轨系统，如何考虑高速滚动接触过程中的材料塑性、表面粗糙度、摩擦、弹性波动等引起的能量耗散对法向接触力和蠕滑力的影响，尚有待于进一步的理论研究和试验验证.

备注：附加材料在中国知网本文的详情页中获取.

致谢：感谢牵引动力国家重点实验室自主研究课题（2020TPL-T02）支持.