基于多种方位角计算方法的超短波AOA 定位比较

马方立 ，徐 扬 ，徐 鹏

（1.西南交通大学计算机与人工智能学院，四川 成都 610031；2.四川省无线电监测站，四川 成都 610052；3.西南交通大学系统可信性自动验证国家地方联合工程实验室，四川 成都 610031；4.西南交通大学数学学院，四川 成都 610031）

无线电发射源的无源定位方法是指定位设备自身不发射无线电信号，而通过测量定位目标所发射信号的参数实现定位的方法.包括以信号到达角度为定位参量的到达角度（angle of arrival，AOA）定位方法、以信号到达时间（time of arrival，TOA）为定位参量的到达时间法、以信号到达时间差（time difference of arrival，TDOA）为定位参量的到达时间差法、以信号到达强度为定位参量的接收信号强度（received signal strength，RSS）法，以及混合定位方法等[1].其中AOA 定位法也称交绘定位法、三角定位法，是指采用三角学的方法，利用多个测向站点的示向度计算信号发射源位置，或者在地图上进行人工交绘的定位方法.对于超短波AOA 定位，被测信号源与监测站之间的距离通常不超过100 km，往往采用平面三角形的方法；但对于短波AOA 定位，被测信号源与监测站之间的距离通常为几百甚至上千公里，平面三角形的方法已不再适用，通常用球面三角形代替平面三角形.这里研究超短波AOA 定位.

文献[2]研究了直角坐标下超宽带的协同AOA定位问题.文献[3]分析了直角坐标下2 站点AOA定位的精确度.文献[4]以线性近似得到的结果作为牛顿迭代的初值，从而降低牛顿迭代法发散的几率，增加了稳定性，提高了算法效率.文献[5-6]研究了地球椭球模型下利用大地坐标进行AOA 定位，算法复杂，难以进行多站点AOA 定位计算.文献[7]研究了大地坐标下的TDOA 定位基于球面精确计算、球面近似计算、等距离正圆柱投影、等角度正圆柱投影和等面积正圆柱投影5 种距离计算方法的精度，并与传统的平面直角坐标TDOA 无源定位模型进行比较.截至到目前，未见有关不同坐标系和不同地图投影方法下AOA 定位性能比较方面的研究文献.

此外，关于测向精确度，按标准测试场地的测试条件，国际电信联盟无线电通信部门（ITU-R）《频谱监测手册》[8]推荐超短波固定测向站均方根值为1°；中国无线电管理机构最新规定值为1°～3°[9].实际上，由于电波传播途径的阻挡、多径效应，以及固定测向站自身的防雷设施影响，测向站的测向误差往往要大得多.因此，有必要研究定位精度与测向精度的关系.

基于此，本文研究如何直接利用大地经纬度进行AOA 定位，并探讨定位精度与角度计算方法的关系.首先研究了方位角计算方法，分析了基于直角坐标的AOA 定位模型，然后提出基于大地经纬度的几种AOA 定位模型，探讨其最优化求解方法，并进行数值仿真验证，给出了不同模型的定位精度，并比较了3 种可用模型对测向误差的敏感性.

1 方位角计算方法

方位角计算是AOA 定位的基础之一.这里将先列出2 种已有计算方法的公式，然后提出4 种近似计算方法.按照业内惯用的方式，方位角以正北为0°和360°，沿顺时针方向增加，正东为90°，正南为180°，正西为270°.

1.1 已有方位角计算方法

1.1.1 基于平面直角坐标的平面法[10]

现有二维AOA 无源定位模型是基于平面直角坐标系的.信号源S发射的信号到达测向站点Mi（i=1,2,···,n，n为侧向站点数）的方位角如式（1）.

式中：（x，y）、（xi，yi）分别为S、Mi的直角坐标；

θti为在站点Mi看信号源的方位角理论值，（°）.

1.1.2 基于大地坐标的球面精确法[11]

按照球面精确法，S到Mi的大圆距离如式（2）.

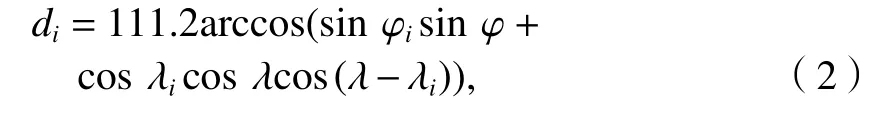
式中：（λ，φ）、（λi，φi）分别为S、Mi的经纬度坐标.

S到Mi的弧度，即到地心的法线夹角的计算如式（3）.

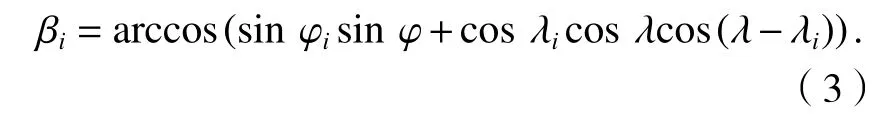
S发射的信号到达Mi的方位角的计算如式（4）.

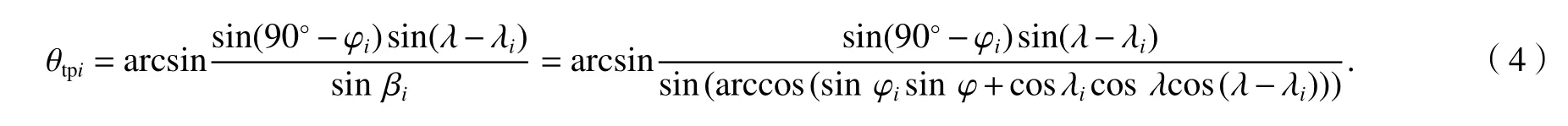
1.2 方位角计算新方法

1.2.1 基于大地坐标的球面近似法

令r为等纬线相对于赤道的尺缩因子，ri为经过测向站点Mi的等纬线相对于赤道的平均尺缩因子[12]，则

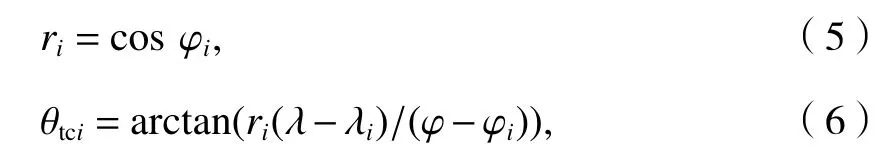
式中：θtci为采用球面近似法方位角的理论预测值.

1.2.2 基于大地坐标的正轴圆柱投影-平面法

文献[13]提出“将大地坐标经Guass 投影反算得到坐标方位角”.Guass 投影计算比较复杂，这里采用简单的正轴圆柱投影.

已有方法中的平面法，其平面直角坐标往往来自平面地图.而平面地图均为地球表面的投影.这里提出正轴圆柱投影-平面近似法的具体操作如下：

以投影平面的横轴为x轴、纵轴为y轴，则等距离投影、等角度（Web Mercater）投影、等面积投影[14-15]3 种球面正轴圆柱投影的横坐标投影均如式（7）.

式中：R为地球平均半径，R=6 371.1 km[13].

而纵坐标的投影公式不同.其中球面等距离正圆柱投影如式（8）.

球面等角度正圆柱投影如式（9）.

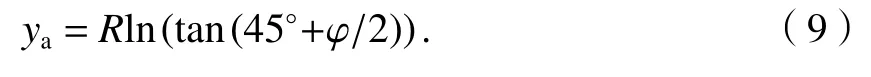
球面等面积正圆柱投影如式（10）.

将式（7）～（10）代入式（1），可分别得到等距离正轴圆柱投影-平面法方位角计算式（11），等角度正轴圆柱投影-平面法方位角计算式（12）和等面积正轴圆柱投影-平面法方位角计算式（13）.

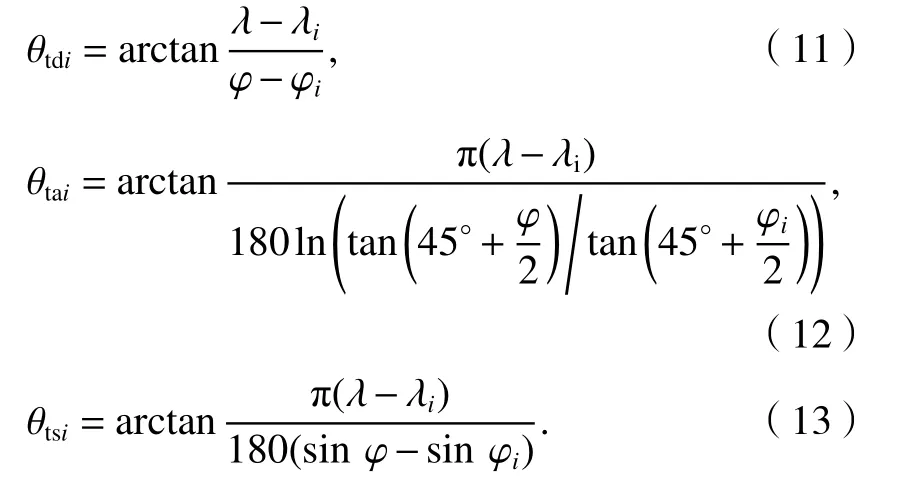
2 平面直角坐标AOA 定位模型

设AOA 定位网有多个无线电测向站点，无线电信号发射源所在地点S.测向站点Mi接收到的信号来波方位角理论值与实测值之差为

式中：θmi为Mi处的信号来波方位角实测值，（°）.

根据式（1），可得定位方程，如式（15）.

如果没有电波传播畸变（反射、折射、绕射等），也没有测向误差，那么2～3 个测向站点就能够准确定位发射源.但实际上不可能.因此，一个测向网可能有更多的测向站点.当测向站点数超过2 时，定位方程组成为超定方程组.

如果n个测向站点能够同时接收到某一信号，且能够同时测得电波到达的方位角，那么最多就可以得到由n个方程组成的定位方程组，如式（16）.

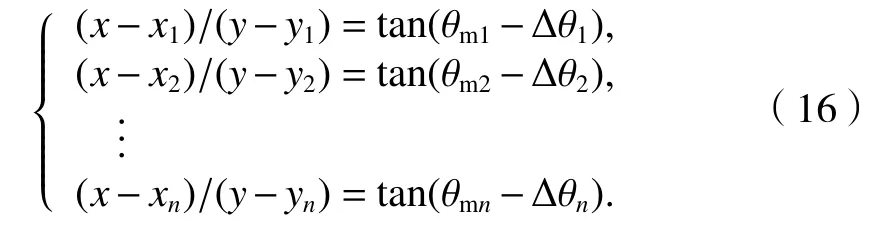
3 大地坐标AOA 定位方程

3.1 球面精确AOA 定位方程

由式（4）、（14）可得定位定位方程组如式（17）.

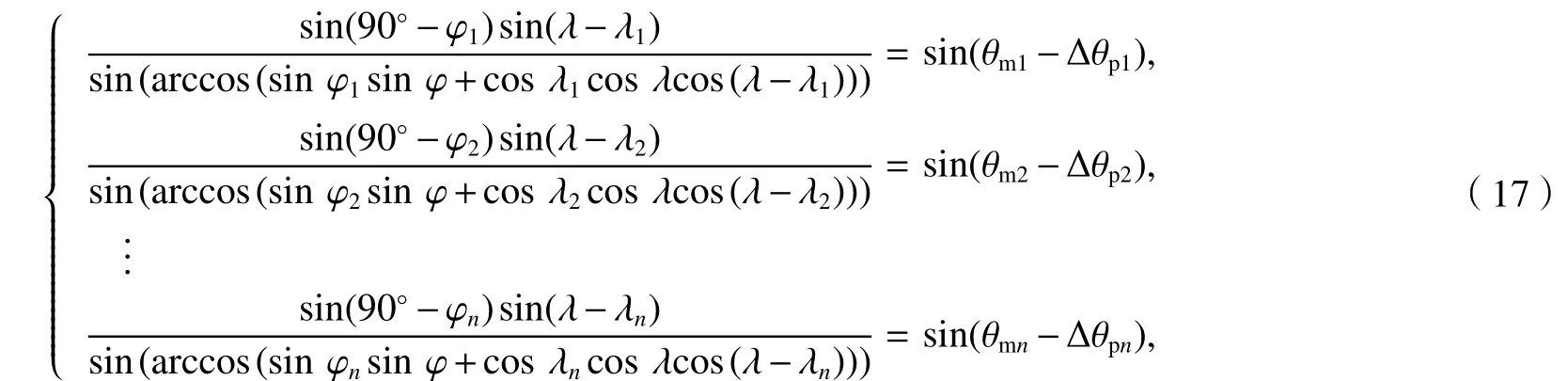
式中：Δ θpi为采用球面精确法得到的 Δ θi.

3.2 球面近似AOA 定位方程

根据式（6）、（14）可得定位方程组如式（18）.

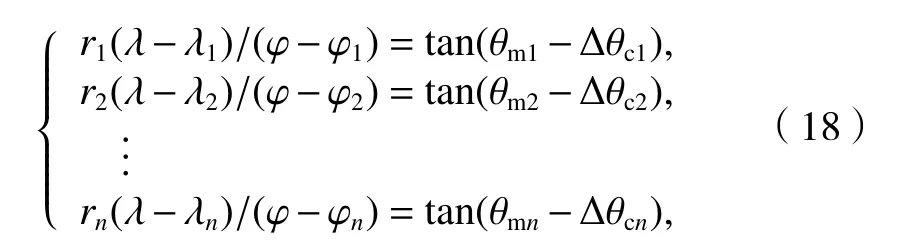
式中：Δ θci为采用球面近似法得到的 Δ θi.

3.3 球面正轴圆柱投影-平面AOA 定位方程

由式（11）、（14）可得球面等距离正轴圆柱投影-平面AOA 定位方程组如式（19）.

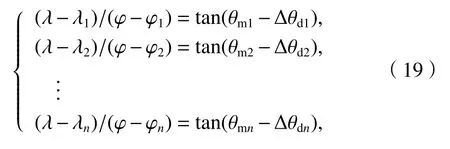
式中：Δ θdi为采用球面等距离正轴圆柱投影-平面法得到的 Δ θi.

由式（12）、（14）可得球面等角度正轴圆柱投影-平面AOA 定位方程组如式（20）.

式中：Δ θai为采用球面等角度正轴圆柱投影-平面法得到的 Δ θi.

由式（13）、（14）可得球面等面积正轴圆柱投影-平面AOA 定位方程组如式（21）.

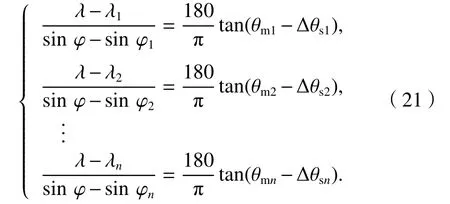
式中：Δ θsi为采用球面等面积正轴圆柱投影-平面法得到的 Δ θi.

4 最优化AOA 定位模型

采用基于无约束非线性规划的最优化定位建模方法[16]，以从信号源的假设位置到达各测向站点的示向度预测值与测向站点实测值之差的累积量为目标函数，以信号源所在地点的经纬度为决策变量.AOA 最优化目标函数为

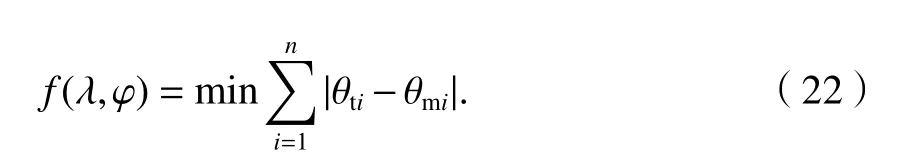
将式（4）代入式（22），可得球面精确AOA 定位模型，如式（23）.

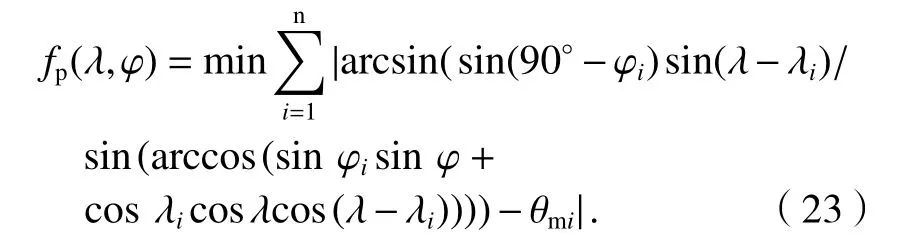
将式（6）代入式（22），可得球面近似AOA 定位模型，如式（24）.

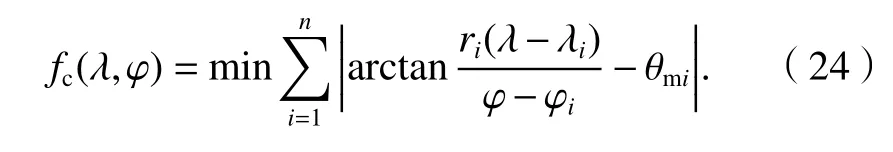
将式（11）代入式（22），可得等距离投影-平面AOA 定位模型，如式（25）.

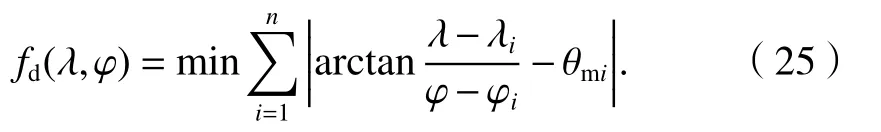
将式（12）代入式（22），可得等角度投影-平面AOA 定位模型，如式（26）.

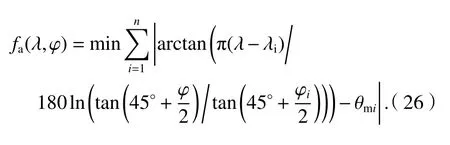
将式（13）代入式（22），可得等面积投影-平面AOA 定位模型，如式（27）.

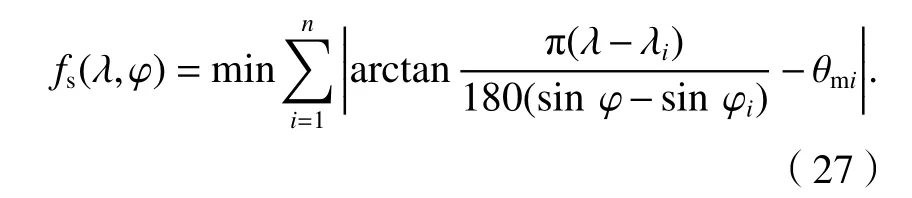
考虑到超短波电波传播的距离通常不超过50 km，假设信号源位于AOA 定位网之内，以AOA定位网的几何中心或者接收到最强信号的站点为中心，以网格逐点搜索法[16]计算最优化目标函数的解，取经线方向和纬线方向各一定的搜索步进计算，收敛性好.网格尺度与定位精度成正比，定位误差均值不超过搜索步进的2 倍.如需提高定位精度，可减小搜索步进.

5 数值验证

通过计算机仿真，基于不同站点数量下的AOA定位模型，比较其在不同测向误差和不同方位角计算方法下的性能.假定各监测站点同步测得来波的示向度.

仿真参数设定如表1.考虑到接近地球南、北两极的纬线尺缩太大，且无人烟，最高纬度只计算到85°.

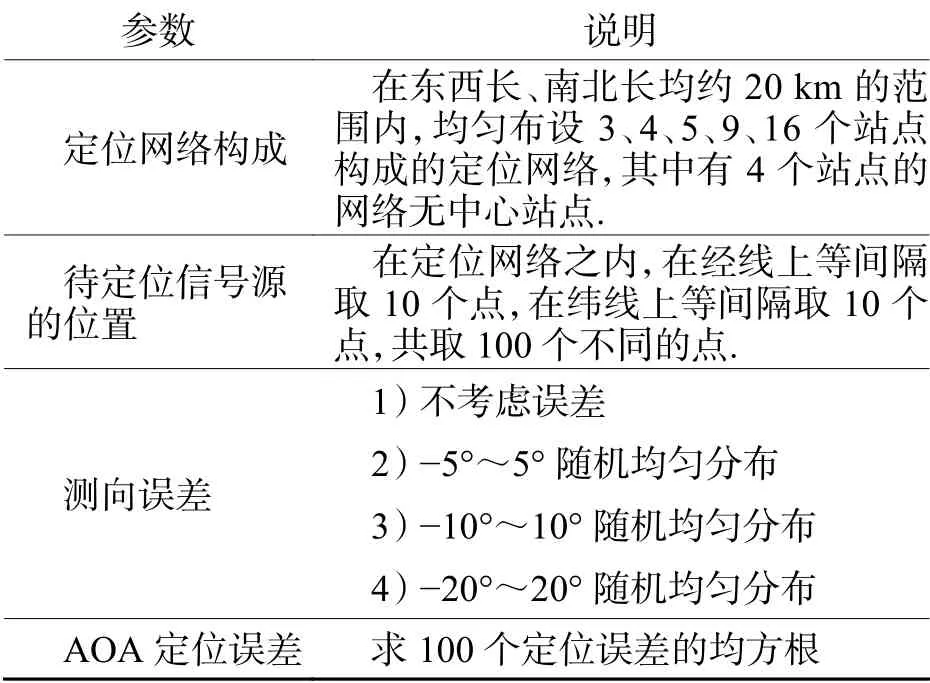
表1 AOA 定位仿真参数设置Tab.1 Setting of simulation parameters in AOA localization

用3～16 个测向站点组成的定位网络进行仿真，以逐点计算的网格搜索方法，获取定位误差结果.考虑到以距离单位表示误差不具有通用性，而百分比表示具有通用性，故以监测网的直径或者边长为分母定义定位精度的百分比，当已知定位网直径时，乘以百分比就可得到具体的距离数据.

5.1 不考虑测向误差时的定位精度比较

5 种方位角计算方法在没有测向误差情况下的比较结果见图1.

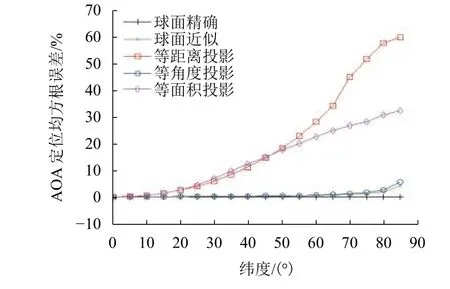
图1 不考虑测向误差时5 种方法的定位精度Fig.1 Localization accuracy of five methods without considering direction-finding error

从中可用看出：当没有测向误差，且不考虑电波传播畸变时，球面精确法无误差.

球面近似计算AOA 定位模型和等角度正圆柱投影-平面AOA 定位模型定位精度接近，在低纬度和中纬度的误差均很小；在高纬度，分别低于4.7%和5.3%，后者略大于前者.

等面积正圆柱投影-平面AOA 定位模型和等距离正圆柱投影-平面AOA 定位模型的定位效果均很差，在低纬度，前者的误差最大可达7%，后者的误差最大可达6%；在中纬度，前者的误差在7%～23%，后者的误差在6%～27%；在高纬度时，前者的误差超过23%，后者的误差超过27%.

因此，等距离正圆柱投影-平面AOA 定位模型和等面积正圆柱投影-平面AOA 定位模型均不可用；球面精确AOA 定位模型、球面近似AOA 定位模型和等角度正圆柱投影-平面AOA 定位模型可用.

5.2 对测向误差敏感性的比较

针对3 种可用的AOA 定位模型进一步仿真.给定 -5°～5°、-10°～10°、-20°～20° 3 种均匀分布的测向误差，3 种模型在不同纬度下的定位精度各进行100 次仿真，得到3、4、5、9、16 个站点定位网的均方根误差见图2～6.

从图2～6 可见对于球面精确AOA 定位模型、球面近似AOA 定位模型和等角度正圆柱投影-平面AOA 定位模型，均有：

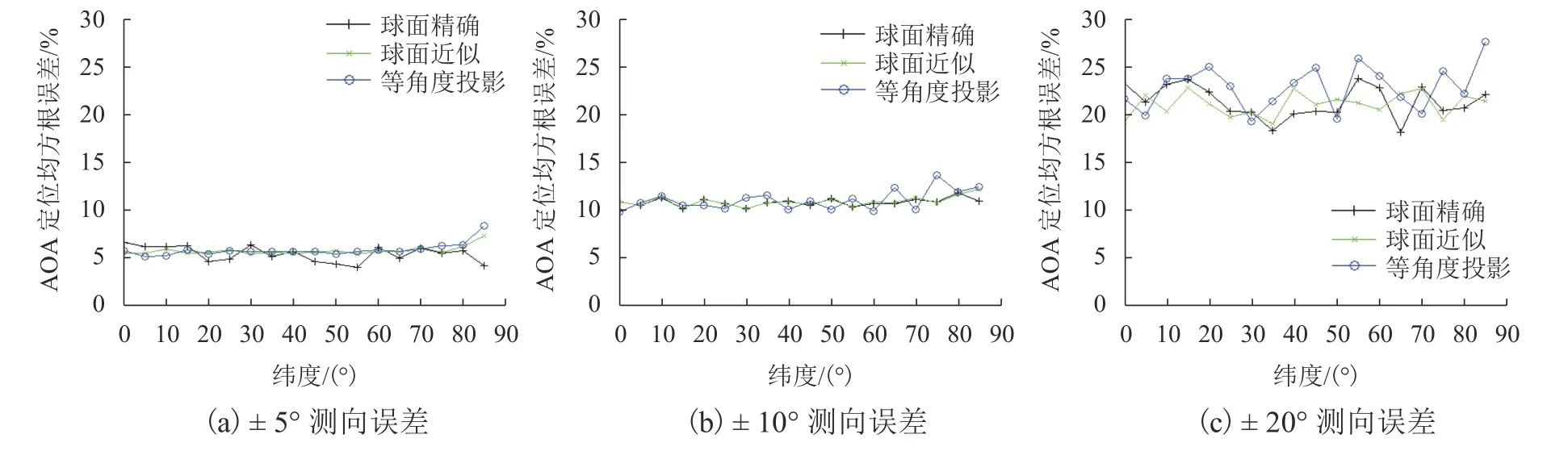
图2 3 站点定位网不同测向误差的定位精度Fig.2 Localization accuracy of different direction-finding errors in 3-station network

1）在相同站点数下，测向误差越小，定位精度越高；

2）在相同测向误差下，测向站点越多，定位精度越高.

3）要提高AOA 定位网的定位精度，既可提高各站点的测向精度，也可增加测向站点数.例如，3 站点、± 5° 测向误差的定位网，9 站点、± 10° 测向误差的定位网，16 站点、± 20°测向误差的定位网的定位精度大致相当.

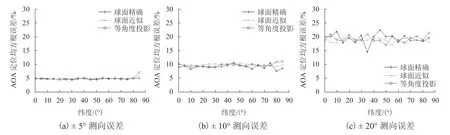
图3 4 站点定位网不同测向误差的定位精度Fig.3 Localization accuracy of different direction-finding errors in 4-station network

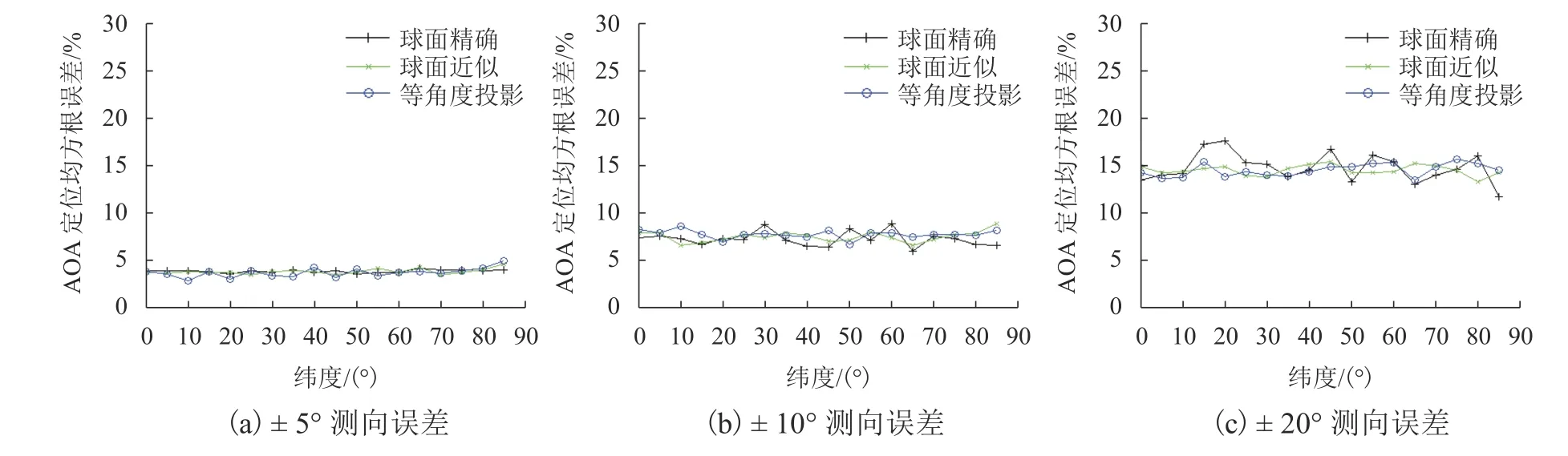
图4 5 站点定位网不同测向误差下的定位精度Fig.4 Localization accuracy of different direction-finding errors in 5-station network

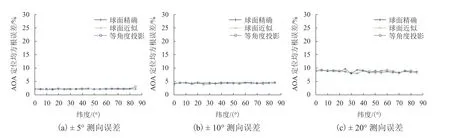
图5 9 站点定位网不同测向误差的定位精度Fig.5 Localization accuracy of different direction-finding errors in 9-station network

图6 16 站点定位网不同测向误差的定位精度Fig.6 Localization accuracy of different direction-finding errors in 16-station network

5.3 AOA 定位模型的运算时效

通过对仿真实验的计时，发现3 种可用模型的定位时效性有差别，其中：球面近似AOA 定位模型的定位运算时间最短，等角度正圆柱投影-平面AOA定位模型是其2.1 倍，球面精确AOA 定位模型是其2.7 倍.

6 结 论

为直接利用大地经纬度坐标进行AOA 定位，本文首先提出了方位角计算的球面近似法和正轴圆柱投影-平面法，进而建立了基于经纬度的到达角度定位方程，并针对球面精确计算、球面近似计算、球面正轴圆柱投影-平面计算几种基于大地经纬度坐标的方位角计算方法的AOA 定位最优化模型，经过建模和计算机仿真，得到如下结论：

1）球面精确AOA 定位模型定位精度最高，且与纬度无关，但其定位运算时间最长，适合要求定位精度高、但时效性要求不高的定位网.

2）球面近似AOA 定位模型和等角度正圆柱投影-平面AOA 定位模型的精度均较高，后者的定位误差略大于前者，且定位运算时间也长于前者.因此，前者比后者更加适合时效性要求高的定位网.

3）要提高AOA 定位网的定位精度，既可提高各站点的测向精度，也可增加测向站点数.

传统的AOA 定位注重单个站的测向精度，本项研究表明，方位角计算方法和站点数量也是定位精度的决定因素.因此，建设无线电定位网需要综合考虑测向精度和站点数量，并应综合考虑定位时效性要求和精度要求，选择合适的AOA 定位模型.