A novel sparse feature extraction method based on sparse signal via dual-channel self-adaptive TQWT

Junlin LI, Huqing WANG,*, Liuyng SONG,b

a College of Mechanical and Electrical Engineering, Beijing University of Chemical Technology, Beijing 100029, China

b Beijing Key Laboratory of High-end Mechanical Equipment Health Monitoring and Self-Recovery, Beijing University of Chemical Technology, Beijing 100029, China

KEYWORDS Complete dictionary;Data transmission;Fault diagnosis;Sparse matrices;Sparse signal;Wavelet transform

Abstract Sparse signal is a kind of sparse matrices which can carry fault information and simplify the signal at the same time. This can effectively reduce the cost of signal storage, improve the efficiency of data transmission, and ultimately save the cost of equipment fault diagnosis in the aviation field. At present, the existing sparse decomposition methods generally extract sparse fault characteristics signals based on orthogonal basis atoms, which limits the adaptability of sparse decomposition. In this paper, a self-adaptive atom is extracted by the improved dual-channel tunable Q-factor wavelet transform(TQWT)method to construct a self-adaptive complete dictionary.Finally, the sparse signal is obtained by the orthogonal matching pursuit (OMP) algorithm. The atoms obtained by this method are more flexible, and are no longer constrained to an orthogonal basis to reflect the oscillation characteristics of signals. Therefore, the sparse signal can better extract the fault characteristics. The simulation and experimental results show that the selfadaptive dictionary with the atom extracted from the dual-channel TQWT has a stronger decomposition freedom and signal matching ability than orthogonal basis dictionaries, such as discrete cosine transform (DCT), discrete Hartley transform (DHT) and discrete wavelet transform(DWT).In addition,the sparse signal extracted by the self-adaptive complete dictionary can reflect the time-domain characteristics of the vibration signals,and can more accurately extract the bearing fault feature frequency.

1. Introduction

The aeroengine works in high-temperature and high-pressure environment,in which the bearing plays the role of supporting load and transmitting motion.1,2The loss of transmission power will be resulted in once the bearing breaks down; this not only causes serious economic loss, but can also result in serious casualties, social environment damage, and other severe consequences.3,4Therefore, the health of bearings is very important for modern aviation equipment.5What’s more,advanced equipment condition monitoring and fault diagnosis technology is widely used to diagnose equipment faults in a timely manner, as well as to implement effective maintenance measures. At present, the main method is to diagnose the vibration signals of rotating equipment.For example,convolutional neural network, the most popular artificial intelligence method,is used by researchers to diagnose faults by transforming bearing vibration signals into images.6Or combined with thermal imaging,CNN is used to classify and identify bearing faults.7

The mathematical theory and method of diagnosis began from time domain and gradually expanded to the time–frequency domain. The diagnosis object gradually expands from the stationary signal to the non-stationary and non-linear engineering signal. Mathematical tools including short-time window Fourier transform(STFT),8time-varying mesh stiffness,9weight-shared capsule network,10deep learning network11,12and sparse component analysis (SCA)13have made good progress in theory and experiments,and reflect the significant role of fault diagnosis technology in equipment safety production.

However,the current diagnosis technology for the real-time fault condition monitoring of bearing, along with the effective fault signal,will produce a large number of redundant normal signals, which brings great cost pressure for data storage and data transmission, and also for the application of sparse signals.14Sparse representation is a new method that has developed rapidly in recent years and has been successfully applied to mitigating impulse interference of aeronautical communication system and to the analysis of big data.15This method attempts to achieve the most concise representation of the original signal through a series of optimal basis functions. Sparse signals are a type of signal composed of sparse coefficients obtained through sparse representation.16The vibration fault signal is a periodic shock signal that meets the requirements of sparse representation; hence, sparse signals can be used for fault diagnosis to effectively solve data redundancy and transmission problems.17Liu et al. improved the measurement matrix by using Weyl inequality and Cauchy’s interleaving theorem, and ultimately realized the recovery of sparse signals.18Li et al. successfully realized target detection and multisource separation based on blind separation and the composite fault detection strategy of signal rank and sparsity using principal component analysis.19Li et al. proposed the augmented deep sparse autoencoder method combined with deep learning to diagnose gear fault.20In recent years, neural network has become a technology that cannot be ignored.21,22

One of the key problems in solving the sparse signal of the original signal is determining how to design a dictionary that not only meets the uniqueness condition, but also meets the sparse requirement. At present, sparse dictionaries are based on orthogonal bases, such as the DCT base, DFT base,23biorthogonal wavelet base,24and flexible analytical wavelet transform (FAWT),25to construct n-dimensional Euclidean space complete dictionaries. The signal is finally decomposed by a sparse coding algorithm such as OMP,26and the sparse signal is obtained to express the fault impact response component,which allows the sparse fault signal to avoid the influence of redundant components. Because the construction of the complete dictionary has a strong theoretical basis,its structure is more compact than overcomplete dictionaries.27In addition,there is no dictionary learning process, its sparse decomposition process is more rapid, and the advantage of saving computational resources has made the complete dictionary more prominent in the era of big data. Wang et al. established an orthogonal sparse dictionary of chirp echo, and realized the high-precision reconstruction of images by using compression sensing technology.28Sandeep et al.used the Gabor dictionary for sparse decomposition,extracted and connected four different features from the atoms of the dictionary,and successfully classified the faults through a least squares twin SVM optimized by PSO.29At present,the sparse decomposition is a fast developing technology,but most of the current research results are focused on compression sensing and signal reconstruction;a series of overcomplete learning dictionaries are used to learn the fault characteristics of a signal, and the original signal is then recovered from the sparse signal. In this paper, by improving the dual-channel adaptive TQWT decomposition method, the dual-channel Q atom is iteratively optimized to obtain the subbands, and the shock response component is extracted from the subbands by using the kurtosis maximum principle as the atom to construct an self-adaptive complete dictionary that matches the fault characteristics. Finally, the sparse signal with time-domain and frequency-domain characteristics is obtained by the OMP sparse decomposition algorithm.30,31To verify the effectiveness of the method,simulation and experimental verification have been shown in this paper. The results demonstrate that, compared with the complete orthogonal basis dictionaries, such as DCT basis,DHT basis and DWT dictionaries,the self-adaptive dictionary can effectively extract sparse signals and identify bearing fault features.

2. Principle of sparse feature extraction

2.1. Dual-channel self-adaptive TQWT

Traditional TQWT changes the value of Q with different characteristics of signal oscillation,and then the signal is filtered by two channel filter banks.It is assumed that the original decomposed signal consists of n independent components:

where xirepresents the subbands with different oscillation characteristics,so the original signal x can be decomposed into a series of subbands with different oscillation characteristics.The oscillation signal can be expressed via wavelet basis function with a high Q factor,and the transient shock signal can be expressed via wavelet basis function with a low Q factor.Fig.1 shows the principle of 3-order TQWT.

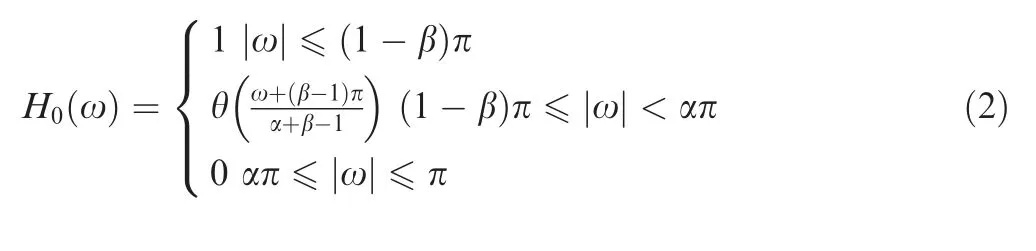
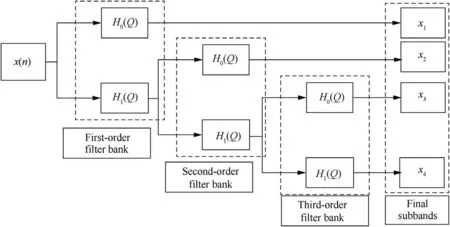
Fig. 1 3-order decomposition diagram of TQWT.

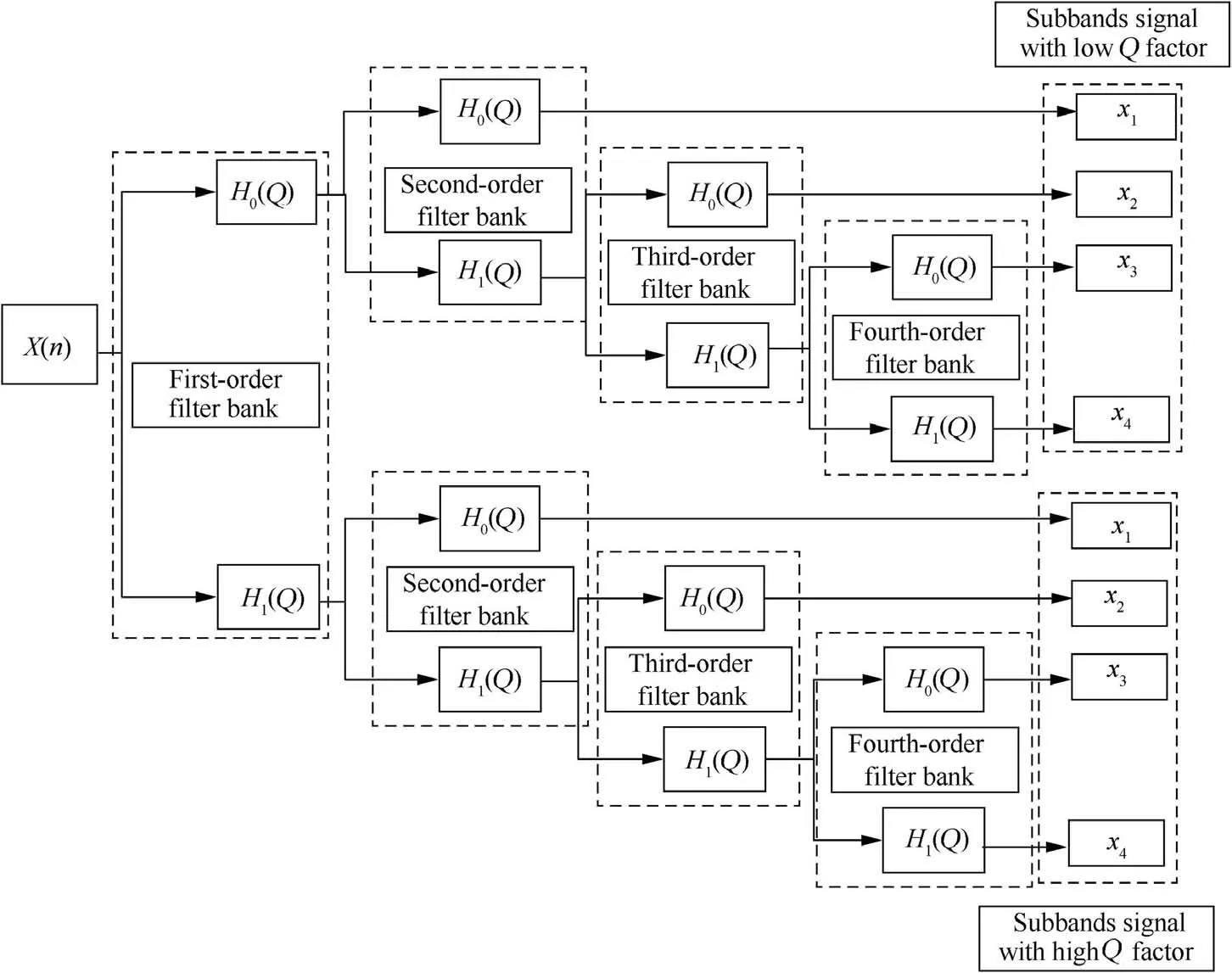
Fig. 2 Principle of dual-channel TQWT decomposition method.

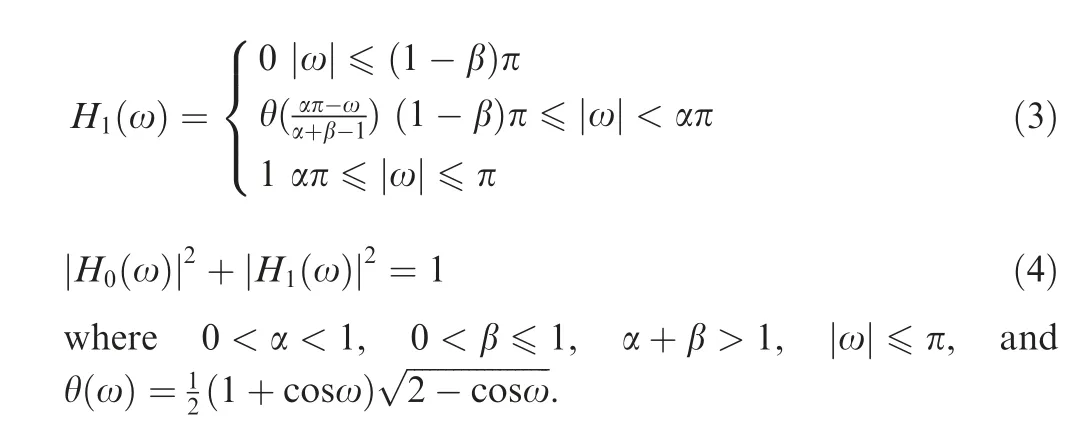
To separate the oscillation characteristics of signals, the low-pass and high-pass filter frequency response functions are as follows:kurtosis principle.Finally,the subband with impact characteristics can be extracted. The principle of dual-channel TQWT decomposition method is shown in Fig. 2.

The improved dual-channel TQWT decomposition method can realize the multi-resolution decomposition of each subband by iterating the Q-factor of the high- and low-order filter channels and optimizing the iterative Q-factor by the maximum

2.2. Decomposition process of sparse signal

The subband with the largest kurtosis is considered to be the optimal subband as the initial signal of the next order filter.Finally, the subband xswith rich shock characteristics is obtained. The shock impact characteristic elements xabis extracted from xsas an adaptive atom, where the subscript ab of xabis the impact response interval.Then the impact atom is extended via Toeplitz transformation to construct an selfadaptive complete dictionary. Finally, On the basis of the self-adaptive dictionary, the original noisy signal is sparse decomposed by OMP method,and the final sparse signal with an impact feature is obtained. The step is shown in Fig. 3.

3. Simulation verification

A simulation signal with impulse characteristics and random white noise interference was as follows:

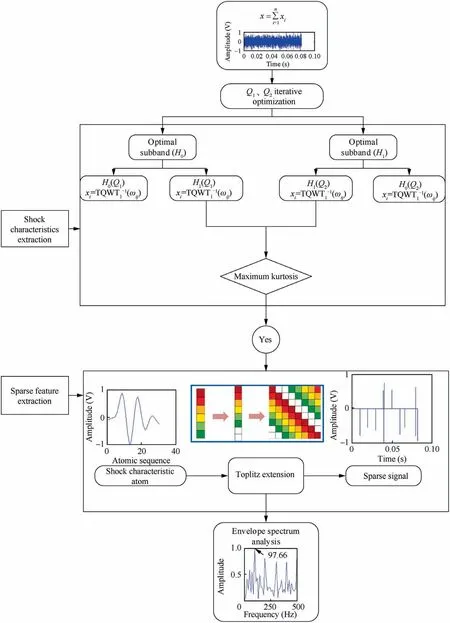
Fig. 3 Flowchart of fault sparse signal diagnosis method based on dual-channel adaptive TQWT.

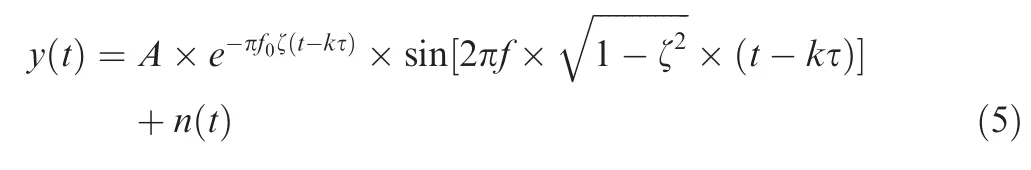
where A represents the amplitude parameter, f0is the oscillation frequency of the signal, ζ represents the damping coefficient, τ is the impact time interval, k is the integer, and n(t)is the white noise.Amplitude(V)is the voltage signal collected by acceleration sensor.

To simulate the strong noise interference in the working condition environment,white noise was added into the original signal, as shown in Fig. 4 (a). Obviously, the periodic impact characteristics have been submerged due to the influence of noise. The envelope analysis of the signal was then carried out, as shown in Fig. 4(b), in which the highest spectral peak is 195.3 Hz and the characteristic frequency of the signal is 97.66 Hz, which has not been effectively enhanced.

Next, the simulation signal was decomposed according to the step shown in Fig. 3 to obtain the sparse signal. The dual-channel TQWT was then used to decompose the original simulation signal.After iterating the Q-factor,the optimal primary oscillation component and the primary subband with a low oscillation component were obtained. The high- and low-oscillation molecules were then processed iteratively to obtain the final optimal subband of the high- and lowoscillation components. Next, the impact component of the optimal subband was extracted to construct a complete dictionary which is suitable for the impact components of the original simulation signal. The impact component in the optimal subband signal was first selected as the atom of the selfadaptive complete dictionary. Next, the atom was then extended by Toeplitz transformation, and finally a selfadaptive complete dictionary with dimensions of 8192×8192 was constructed.

To compare the effectiveness of the method, complete orthogonal basis dictionaries of DCT and DHT with the same dimensions were constructed for comparison experiments.Atomic waveforms of simulated signal with three complete dictionaries are shown in Fig.5(a)–(c).The simulation signal was sparsely decomposed on the complete dictionary by the OMP method,and the final sparse signal is shown in Fig.6.Then the sparse signal is analyzed (Fig. 6), and the sparse signal obtained by the dual-channel adaptive TQWT method clearly reflected the impact characteristics at the time of fault occurrence. Envelope analysis was carried out, and the results are presented in Fig. 7. It is clear that the fault characteristic frequency of 97.66 Hz is the highest peak at this time.Compared with Fig. 4(b), the characteristic frequency in the envelope spectrum was enhanced,and the frequency-domain fault characteristics of the sparse signals were verified.

4. Experimental verification

To further verify the practicability and reliability of this method, an experimental platform was built, as shown in Fig. 8. The test object was an NTN Nu 204 bearing. Grooves with a width of 0.25 mm and depth of 0.07 mm, and with a width of 0.15 mm and depth of 0.05 mm, were processed in the inner and outer bearing rings via laser. The experimental platform was driven by a 1300 r/min motor, and the acceleration sensor was used to collect the original experimental signal.The sampling frequency was 100 kHz. Table 1 lists the fault characteristic frequency of the fault bearing.

4.1. Sparse decomposition results of inner race fault

4.1.1.Sparse feature extraction and diagnosis of inner race fault

First, the inner race fault bearing was used for experimental verification. The collected vibration signal is shown in Fig. 9(a). It can be seen that the weak impact characteristics were submerged in the noise after the vibration signal was interfered by the noise.The results of envelope demodulation analysis are presented in Fig. 9(b), in which the identified peak frequency was 189.2 Hz, 244.1 Hz and 293 Hz, which are quite different from the theoretical fault frequency; therefore, the noise had a relatively obvious impact on the experimental signal.

Therefore, according to the flowchart in Fig. 3, the experimental signal was sparsely decomposed, and the sparse signal was extracted. The atom obtained is used to build a complete dictionary through the Toplitz extension,and sparse decomposition is carried out according to the method shown in Fig.10.Fig. 11 shows the sparse decomposition results by the dualchannel adaptive TQWT complete dictionary;Fig.12 displays the sparse decomposition results by the DCT dictionary;Fig. 13 displays the sparse decomposition results by the DHT dictionary; Fig. 14 displays the sparse decomposition results by the DWT dictionary.

The extracted atoms are shown in Figs. 11(a)–14(a). From the perspective of the atom obtained, the atom of the dualchannel adaptive TQWT has more flexible matching. As a complete dictionary of comparative analysis, the atoms of the three dictionaries are all composed of orthogonal bases such as trigonometric functions or wavelet bases,which belong to the traditional orthogonal basis atoms, and do not have oscillation characteristics. The sparse signal is obtained, as shown in Figs. 11(b)–14(b). Among them, the sparse signal of DCT dictionary shows the characteristics of aggregation,not the ideal sparse signal. The others are ideal. Combined with the results of envelope analysis,it is evident that the proposed method can effectively extract the fault feature frequency (146.5 Hz). Compared with the theoretical value of bearing fault, the fault features identified by the envelope frequencies of the DCT, DHT and DWT dictionaries can be judged as false frequencies; hence, thee dictionaries cannot effectively identify the fault features.

Fig. 4 Waveform and envelope spectrum of simulated signal.

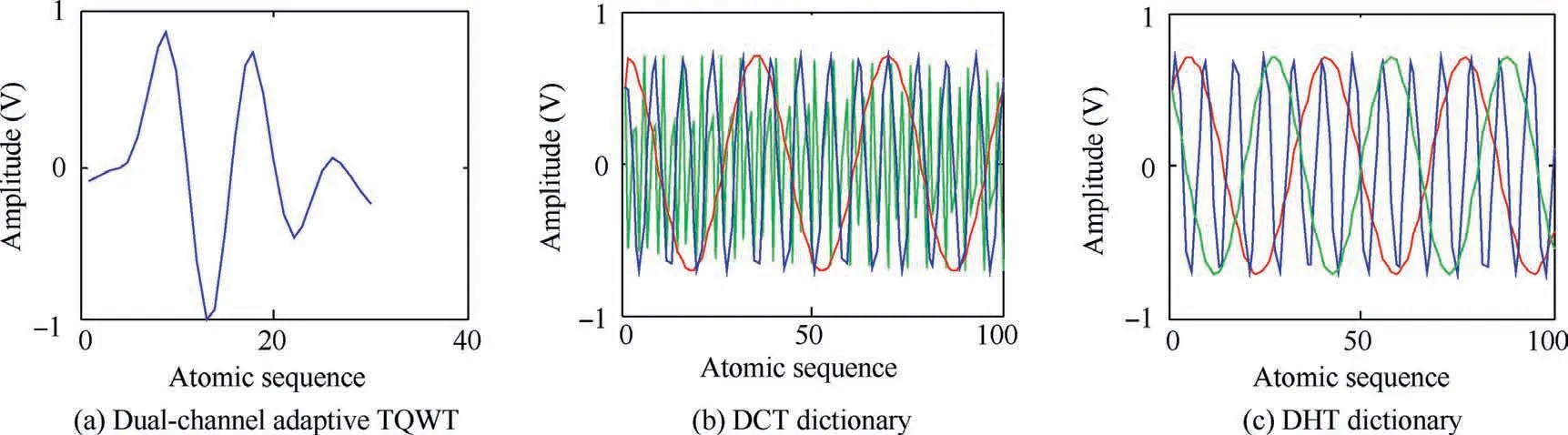
Fig. 5 Atomic waveforms of simulated signal with three complete dictionaries.

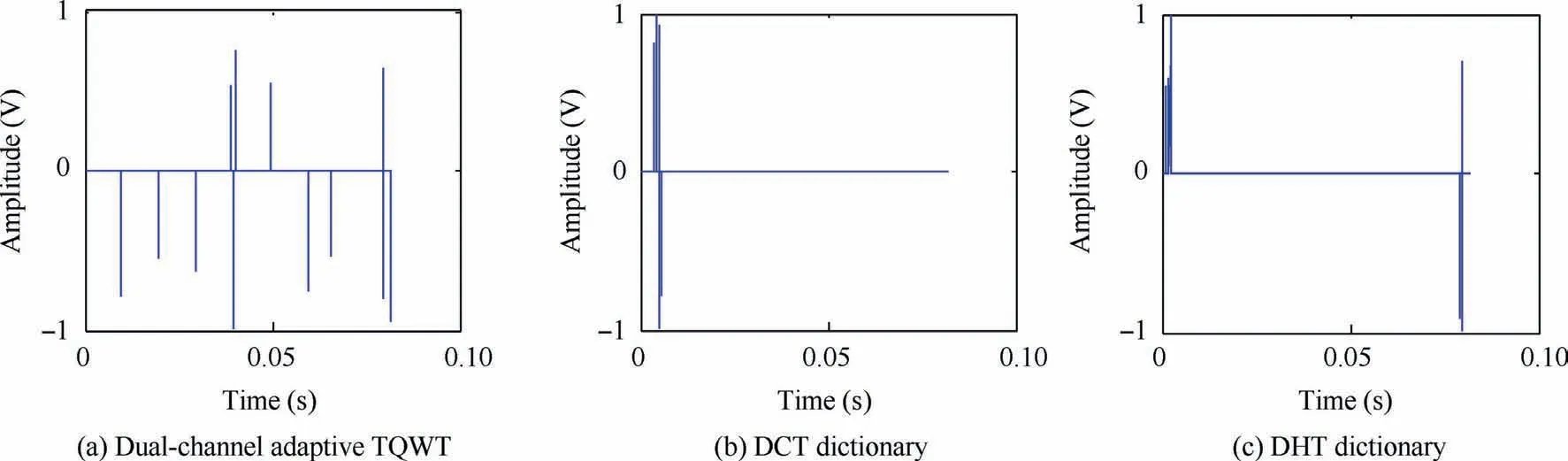
Fig. 6 Sparse signal of simulated signal with three complete dictionaries.

Fig. 7 Envelope spectrum of simulated sparse signals with three complete dictionaries.

Fig. 8 Test rig and fault bearing.

Table 1 Fault characteristic frequency of fault bearings.

4.1.2.Sparse feature extraction and diagnosis of inner race fault with strengthened noise

In order to study the influence of noise on sparse signal, the bearing signal is further studied after the noise is strengthened.As shown in Fig. 15, when the noise is strengthened, the impact characteristics in the inner race signal become less obvious. The envelope spectrum shows that there are 189.2 Hz,293 Hz, 390.6 Hz and other high-frequency noise interference.

The process is the same as that in Section 4.1.1,and Fig.16 shows the decomposition results of sparse dictionary. The atoms of the dual-channel adaptive TQWT complete dictionary are more irregular and have the characteristics of oscillation and attenuation. Envelope analysis of sparse signals is performed, as shown in Fig. 16(c). 146.5 Hz is the spectrum peak, at which the fault characteristics of the bearing inner race signal can be extracted.

Through the envelope analysis of the sparsity of each dictionary, it can be found that the feature frequencies extracted by the dictionary as a comparative analysis are all false frequencies as shown in Fig. 17.

4.2. Sparse decomposition results of outer race fault

4.2.1. Sparse feature extraction diagnosis of outer race fault

To verify the robustness of the proposed method, the experimental bearing with outer fault race was further analyzed,and the analysis steps were the same as those of the inner fault race experiment. As shown in Fig. 18, it can be seen that the time-domain impulse characteristic of the signal was disturbed by the noise. The fault characteristic frequency of 85.45 Hz in the envelope spectrum was also interfered by the peak value of 152.6 Hz.In addition,there are other high-frequency noise frequencies that interfere with the fault characteristic frequencies,such as 262.5 Hz,421.1 Hz and 470 Hz,so the fault characteristics could not be accurately diagnosed.

The experimental signal of the outer race of the fault bearing was analyzed according to the flowchart in Fig. 3, and Fig. 19(a) is the extracted atom. The extracted atom in this experiment still presents obvious oscillation characteristics.Fig. 19(b) shows the sparse signals obtained by OMP sparse decomposition via the dual-channel adaptive TQWT complete dictionary. By observing the envelope spectrum, it can be found that the peak of 85.45 Hz is the characteristic frequency of the fault bearing. Therefore, in the outer race experiment,the fault frequency of bearing is still successfully extracted by the dual-channel adaptive TQWT complete dictionary.

Fig.20 shows envelope spectrum of the other three comparison dictionaries.Due to the lack of enough adaptability of the orthonormal atom, it cannot meet the sparse signal requirements of the outer ring bearing.So the final envelope spectrum shows that the extracted fault frequency is false frequency.

4.2.2. Sparse feature extraction diagnosis of outer race fault with strengthened noise

When the noise is enhanced, it can be seen that the timedomain signal has been seriously affected by the noise, and there are 238 Hz and 476.1 Hz high-frequency noise in the envelope spectrum, as shown in Fig. 21(b).

Fig. 22 and Fig. 23 show the analysis results of the dualchannel adaptive TQWT complete dictionary and three comparison dictionaries. It can be seen that the atoms of the dual-channel adaptive TQWT complete dictionary still have the characteristics of oscillation and attenuation under the influence of enhanced noise.As for other dictionaries for analysis and comparison,because they are dictionaries of orthogonal basis, atoms are still consistent with the previous analysis.Therefore,as a comparison of the three dictionaries,the envelope analysis results of DCT, DHT and DWT are not satisfactory due to the limitation of orthogonal basis.At this time,the envelope spectrum of the dual-channel adaptive TQWT complete dictionary can accurately extract 85.45 Hz characteristic frequency.

Fig. 9 Waveform and envelope spectrum of inner race fault signal of inner race fault.

Fig. 10 Process of sparse decomposition.

Fig. 11 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of inner race fault.

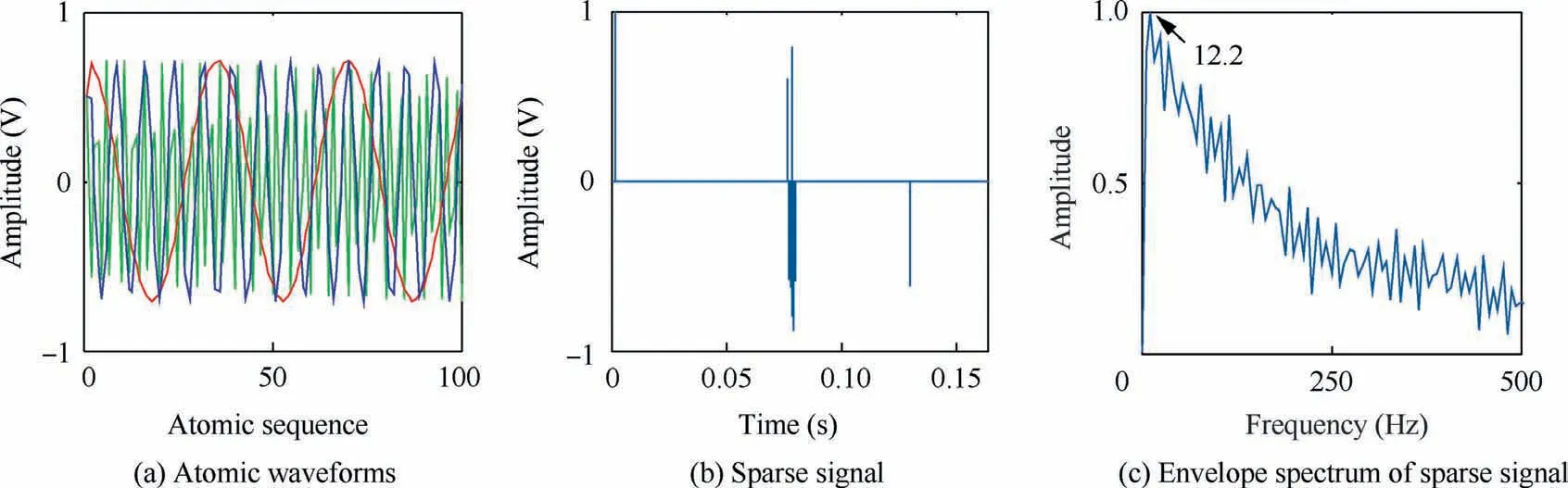
Fig. 12 DCT dictionary’s sparse decomposition results of inner race fault.

Fig. 13 DHT dictionary’s sparse decomposition results of inner race fault.

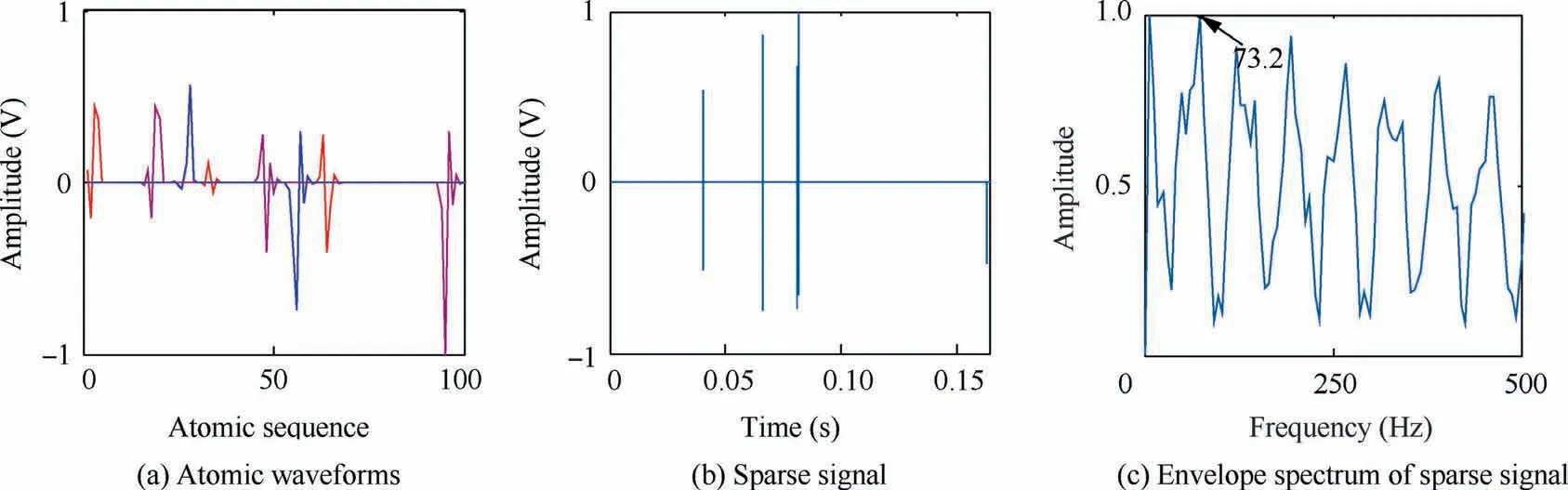
Fig. 14 DWT dictionary’s sparse decomposition results of inner race fault.

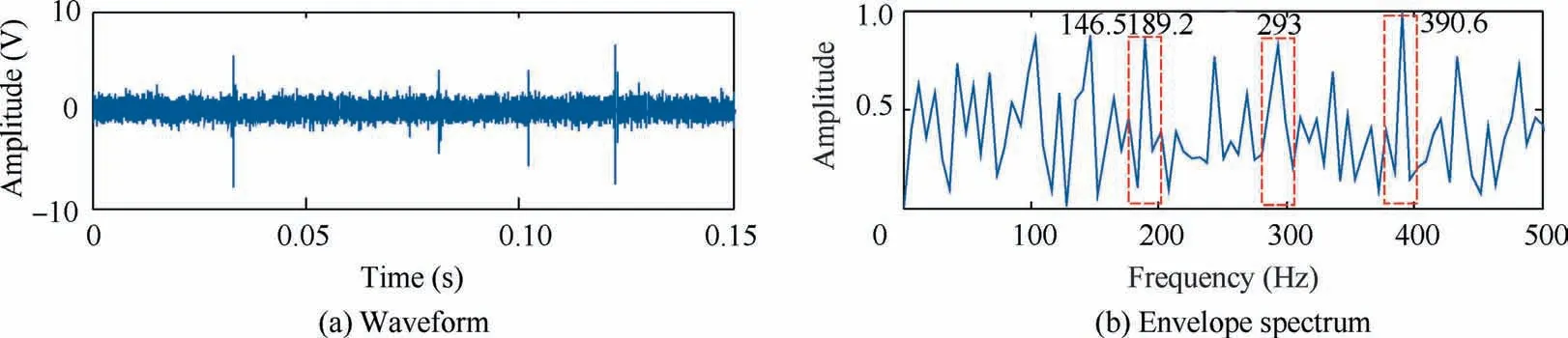
Fig. 15 Waveform and envelope spectrum of inner race fault signal with strengthened noise.

Fig. 16 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of inner race fault with strengthened noise.

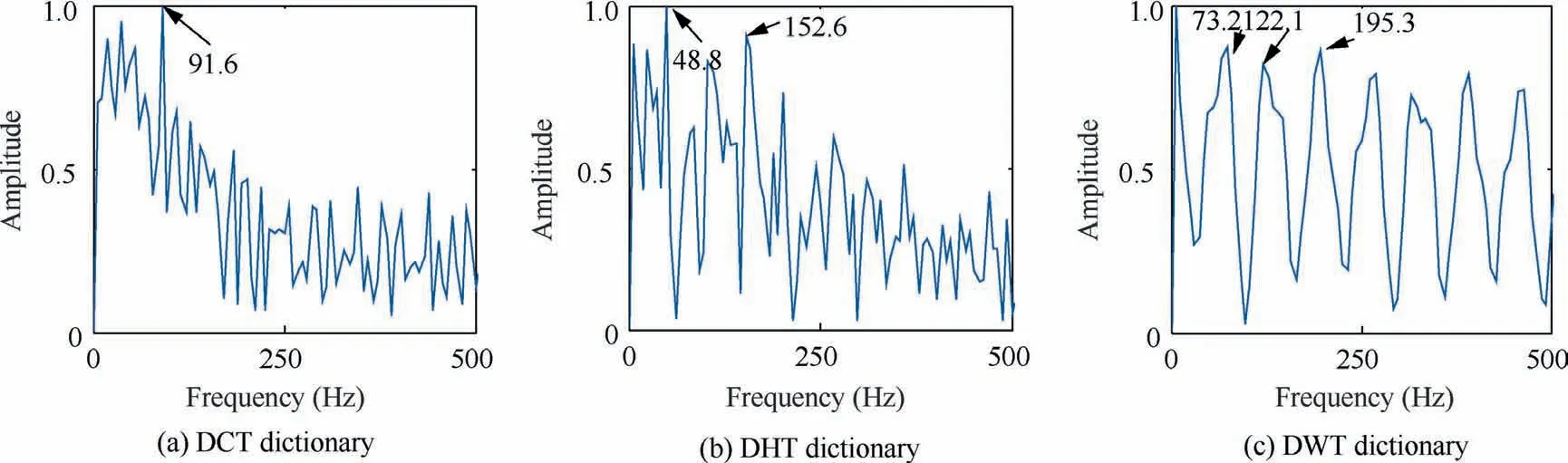
Fig. 17 Envelope spectrum of inner race fault with strengthened noise for three kinds of comparative dictionaries.

4.3. Sparse decomposition results of ball fault

4.3.1. Sparse feature extraction diagnosis of ball fault

In order to analyze the fault more comprehensively, the ball bearing data of Case Western Reserve University (CWRU)are used to verify the method.The ball bearing fault data with fault size of 21 inches and rotating speed of 1772 r/min are used. The characteristic frequency of ball fault is about 139 Hz. The time-domain diagram and envelope spectrum of the ball are shown in Fig.24.It can be seen from the envelope results that there are two strong interference frequencies 130.4 Hz and 159.7 Hz that affect the extraction of fault characteristic frequency (Fig. 25).

In the ball experiment, the extracted atoms still have the characteristics of oscillation and attenuation, which shows the flexibility of non-orthogonal basis. And through envelope analysis, 136.2 Hz as fault feature frequency can be easily extracted, and there is no high-frequency noise frequency to affect the extraction of fault feature frequency (Fig. 26).

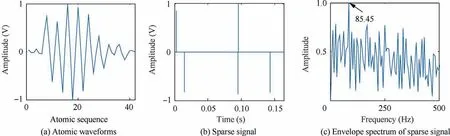
Fig. 19 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of outer race fault.

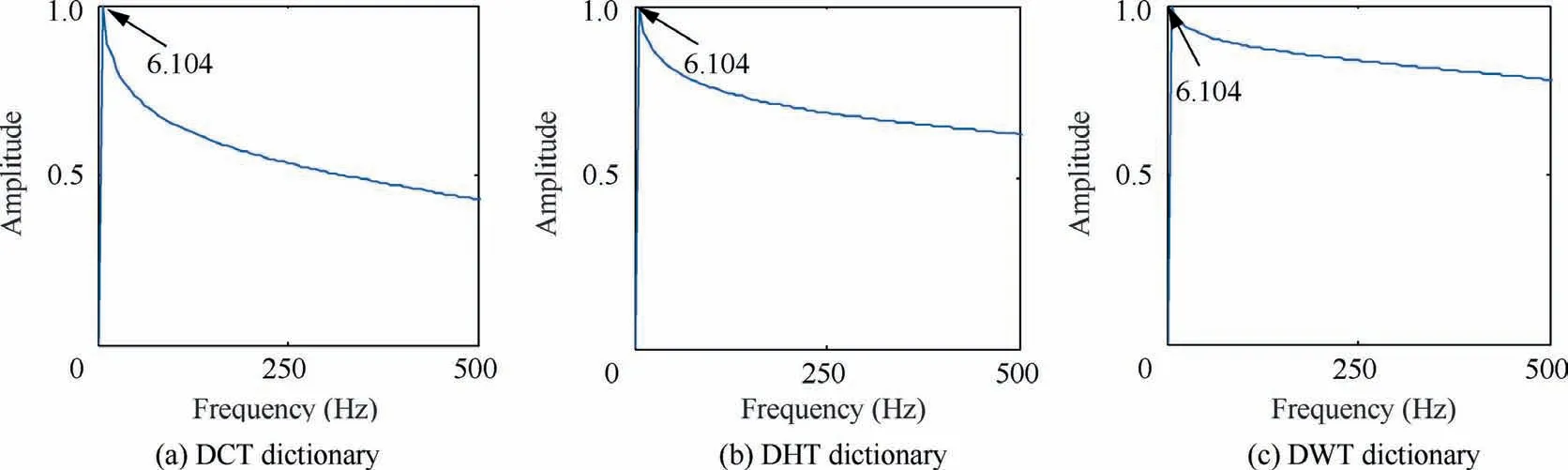
Fig. 20 Envelope spectrum of outer race fault for three kinds of comparative dictionaries.

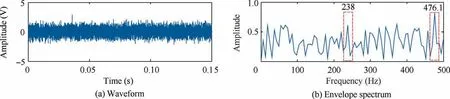
Fig. 21 Waveform and envelope spectrum of outer race fault signal with strengthened noise.

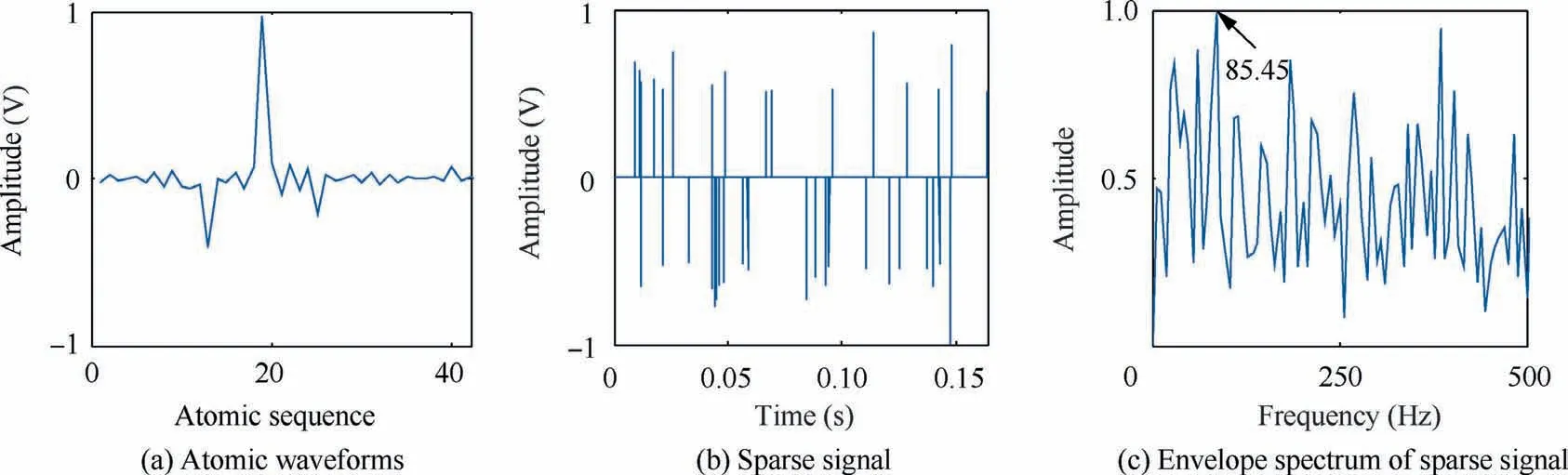
Fig. 22 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of outer race fault with strengthened noise.

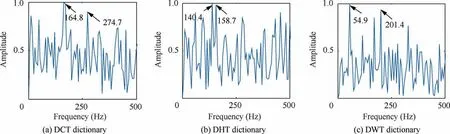
Fig. 23 Envelope spectrum of outer race fault with strengthened noise for three kinds of comparative dictionaries.

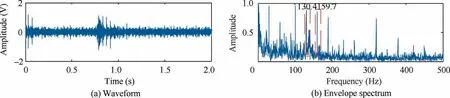
Fig. 24 Waveform and envelope spectrum of ball fault signal.

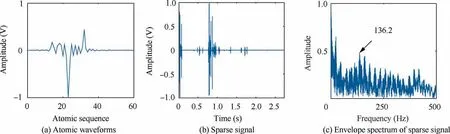
Fig. 25 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of ball fault.

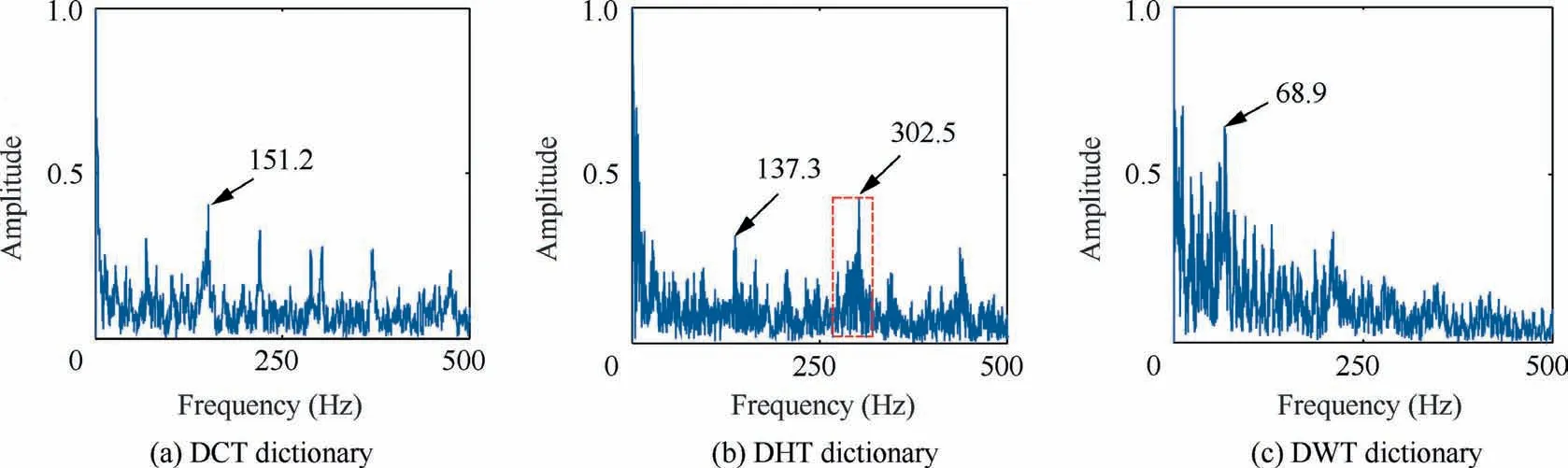
Fig. 26 Envelope spectrum of ball fault for three kinds of comparative dictionaries.

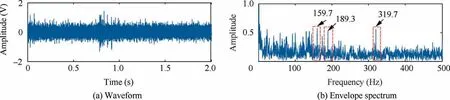
Fig. 27 Waveform and envelope spectrum of ball fault signal with strengthened noise.

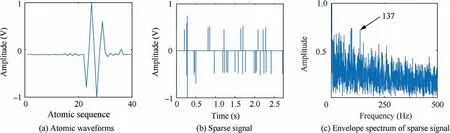
Fig. 28 Dual-channel adaptive TQWT complete dictionary’s sparse decomposition results of ball fault with strengthened noise.

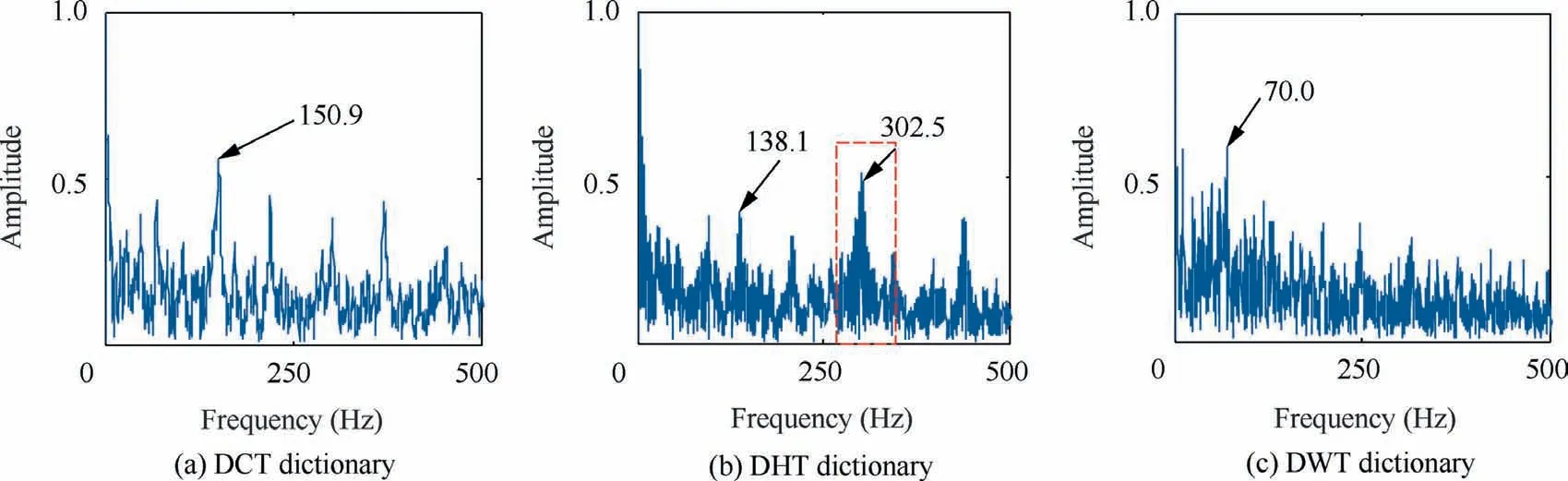
Fig. 29 Envelope spectrum of ball fault with strengthened noise for three kinds of comparative dictionaries.

In the comparative analysis,only the sparse decomposition results of DHT dictionary can extract 137.3 Hz. This shows that as a basic non-redundant decomposition method, the orthogonal basis dictionary can extract the fault feature frequency in some fault diagnosis occasions, but it should be noted that there is still 302.5 Hz high-frequency noise interference at this time. The frequency extracted by the other two orthogonal basis dictionaries is 151.2 Hz and 68.9 Hz respectively, which is too different from the fault feature frequency,so it can be regarded as false feature frequency.

4.3.2. Sparse feature extraction diagnosis of ball fault with strengthened noise

For the integrity of this study, random noise is applied to the ball signal to observe the performance of this method under the influence of noise. As shown in Fig. 27, the time-domain impact characteristics of the spherical signal have been submerged, and there are multiple high-frequency noise effects on the envelope spectrum.

Fig. 28 displays the sparse decomposition results by the dual-channel adaptive TQWT complete dictionary. It can be seen that, under the influence of noise, this method has also achieved good results in the ball experiment: The extracted atoms have oscillation and attenuation characteristics; sparse signal has sparse characteristic,and there is no clustering characteristic;envelope spectrum analysis shows that the characteristic frequency 137 Hz has no high-frequency noise effect.

Similar to Section 4.3.1, the three dictionaries are still used for comparative analysis.As shown in Fig.29,compared with the other two dictionaries, DHT dictionary can be considered to extract fault features at 138.1 Hz when the ball experiment is noisy. Similarly, there is a high-frequency noise 302.5 Hz.The envelope result of dual-channel adaptive TQWT complete dictionary has no interference of high-frequency noise. This shows that the sparse signal of the dual-channel adaptive TQWT complete dictionary has better noise immunity while extracting fault feature frequency.

5. Conclusions

The method proposed in this paper draws on the idea of the dual-channel, multi-order, iterative Q-factor, and ultimately uses the impact feature in the subband as an atom to construct an adaptive complete dictionary for sparse decomposition.The method has been verified by simulation and experiment, and the results prove that the method can extract sparse feature under noise interference to obtain sparse signals, and that sparse signals have good time-domain impact and frequencydomain characteristics.

This method can effectively match the oscillation characteristics of the signal, can liberate the signal decomposition from the traditional orthogonal basis and overcomplete redundancy decomposition, and has greater flexibility and adaptability.Moreover, the sparse signal can be compressed into several sparse signals without losing the impact characteristics of the original signal, thereby reducing the data by two to three orders of magnitude and providing a new research direction and theoretical support for the storage and transmission of industrial big data.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by the National Key R&D Program of China (Grant No. 2018YFB1503103).