Polynomial networks based adaptive attitude tracking control for NSVs with input constraints and stochastic noises

Xiohui YAN, Mou CHEN, Shuyi SHAO, Qingxin WU

a College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

b School of Artificial Intelligence and Big Data, Hefei University, Hefei 230601, China

KEYWORDS Backstepping control;Input constraints;Multi-dimensional Taylor Polynomial Networks(MTPN);Near Space Vehicles (NSVs);Stochastic input noises

Abstract This paper proposes a backstepping technique and Multi-dimensional Taylor Polynomial Networks (MTPN) based adaptive attitude tracking control strategy for Near Space Vehicles(NSVs) subjected to input constraints and stochastic input noises. Firstly, considering the control input has stochastic noises,and the attitude motion dynamical model of the NSVs is actually modeled as the Multi-Input Multi-Output(MIMO)stochastic nonlinear system form.Furthermore,the MTPN is used to estimate the unknown system uncertainties,and an auxiliary system is designed to compensate the influence of the saturation control input.Then,by using backstepping method and the output of the auxiliary system,a MTPN-based robust adaptive attitude control approach is proposed for the NSVs with saturation input nonlinearity, stochastic input noises, and system uncertainties. Stochastic Lyapunov stability theory is utilized to analysis the stability in the sense of probability of the entire closed-loop system. Additionally, by selecting appropriate parameters,the tracking errors will converge to a small neighborhood with a tunable radius.Finally,the numerical simulation results of the NSVs attitude motion show the satisfactory flight control performance under the proposed tracking control strategy.

1. Introduction

In the last few decades, the robust nonlinear flight control problem becomes one of focused research topics and has been extensively investigated.1–4Meanwhile, several flight control methods have been developed, such as robust nonlinear control, anti-disturbance control, fault-tolerant control, etc., and some meaningful research results can be found in Refs.5–7.Compared to ordinary flight vehicles, Near Space Vehicles(NSVs) have many advantages, such as wide envelope,multi-tasking ability, low maintenance cost, and high-speed flight.NSVs have gradually become the frontier research focus of the national defense and attracted more and more attention.In Ref.8, the twelve states equations of NSVs under the variable wind field were derived, and an adaptive Nonlinear Generalized Predictive Control (NGPC) scheme was proposed based on the B-spline recurrent functional link network.Based on the switched systems and Fuzzy Logic Systems (FLSs), a robust tracking controller was designed for the variable structure NSVs with external disturbances.9In Ref.10, a neural adaptive optimal longitudinal tracking control approach was designed for the NSVs with uncertainties and disturbances.However,owing to the special flight environment and the complex characteristics of the NSVs, the tracking control problem of the NSVs still be a challenging research task and need to be further studied.

Actually,there exist many unknown system uncertainties in the NSVs control system. Based on the function approximation theory, FLSs or Neural Networks (NNs) are the extremely effective approximators which always be used to estimate the unknown functions of uncertain systems.Furthermore,a large number of approximation based control schemes have been developed for uncertain strict-feedback nonlinear systems, for example, Single-input and Single-output (SISO)systems,11–15MIMO systems.16–18In particular, combining backstepping method with NNs, a neural adaptive control allocation strategy was presented for the NSVs with system uncertainties and external disturbances.19In Ref.20, a reliable fuzzy control approach was designed for hypersonic vehicle subjected to stochastic actuator failures. In Ref.21, a discrete-time nonlinear adaptive controller was developed for the generic hypersonic flight vehicle based on feedback linearization method and neural network approximation.Although these FLs or NNs based control methods provide good performance, more efficient control design approaches are still needed to improve the control time-effectiveness.Based on the advantages of good realtime performance and easy implementation, the MTPN based adaptive control schemes were proposed for nonlinear system.22,23

To be able to design the constrained control scheme for nonlinear systems, some robust control schemes have attracted extensive attentions. As a kind of non-smooth nonlinearities, input saturation often occurs in a large amount of real engineering systems, and it is hard to be tackled during the controller design. The research of constrained control problem of nonlinear systems is of great theoretical significance and application value. In the past decades, many robust constrained control schemes have been presented for uncertain nonlinear systems in the presence of input constraints.24–32In Ref.24, by utilizing backstepping control method, a robust constrained controller was designed for uncertain nonlinear systems in the presence of symmetric input saturation. By designing an auxiliary system to compensate the influence of input saturation and combining with Radial Basis Function Neural Networks (RBFNNs), a robust adaptive constrained control method was presented for a class of MIMO systems with nonsymmetric saturation input nonlinearities.25By constructing a Sigmoid-based nonlinear smooth function to replace the saturation input, a High Order Disturbance Observer (HODO) based fuzzy constrained control approach was proposed for uncertain nonlinear systems.26In Ref.27, by designing a Tanh-based smooth nonlinear function to replace the saturation input and combining with FLSs, an adaptive fuzzy tracking control strategy was developed for the pure-feedback stochastic systems with input saturation. In Ref.28, by introducing Nussbaum functions and the designed auxiliary system, a backstepping and FLSs based direct adaptive control scheme was proposed for nonlinear systems with system uncertainties and input saturation. The constrained control problem of MIMO nonlinear systems with input/state constraints was investigated, and an online optimization based robust constrained control strategy was proposed.29In Ref.30, by incorporating Dynamic Surface Control (DSC) technique to the recursive design, a NNs-based robust tracking controller was designed for nonlinear SISO stochastic systems in the presence of input saturation, and all the closed-loop signals were Semi-globally Uniformly Ultimately Bounded(SGUUB) in probability. In Ref.31, by introducing the prescribed performance functions and auxiliary systems, the constrained tracking control problem for NSVs with input and output constraints was discussed, and a robust constrained control strategy was designed. However, external disturbances and internal noise disturbances need to be considered which always affect the flight control performance of NSVs with input saturation.

Recently, for the purpose of exploiting interference information, various observers can be designed to estimate the external disturbances. The output of the disturbance observer always be utilized to compensate the effect of external disturbances, and the robust control performance can be improved.In the past few years, various types of disturbance observers has been developed,and large amounts of Disturbance Observer Based Control (DOBC) strategies were proposed for MIMO nonlinear systems.32–36However, as is well-known,the influence of stochastic disturbances is inevitable in practical mechanical systems, which will make the design of the robust controller more difficult. For instance, in Ref.37, an adaptive robust stochastic control strategy was developed for Lagrangian systems with stochastic noise. Nevertheless, the design of the constrained control scheme for the NSVs control system with stochastic input disturbances has not been considered. Therefore, the design of the robust tracking controller based on MTPN and auxiliary system for NSVs with stochastic input noises and input constraints will be further studied,which motivates this study.

In this paper, based on MTPN and auxiliary system, an adaptive attitude tracking control strategy is proposed for the NSVs with input constraints and stochastic input noises.Firstly, an attitude motion dynamic of the NSVs is modeled as the MIMO stochastic nonlinear system. The auxiliary system are introduced to tackle the effect of input saturation.Furthermore, the output of the MTPN is utilized to compensate the influence caused by the unknown system uncertainties.Finally, by utilizing backstepping method, an adaptive constrained stochastic control approach using MTPN is presented for the NSVs with stochastic input noises and saturation control input. Our major contributions of this work can be listed as follows:

(1) Considering the influence of the stochastic input noise disturbances,and according to stochastic theory,a novel attitude motion dynamic of the NSVs is modeled as the MIMO stochastic nonlinear system.

(2) The MTPN is first introduced to approximate the unknown function terms of the flight control system,and easy implementation can be obtained.

(3) By utilizing backstepping control technique and stochastic control method, a robust stochastic constrained attitude tracking controller is designed, and all the closed-loop signals are semi-globally uniformly ultimately bounded in probability. Furthermore, the tracking errors will converge to a small neighborhood with a tunable radius by adjusting some design parameters.

In the rest of this paper, based on stochastic theory, a MIMO stochastic nonlinear system model of the NSVs is obtained, and the detailed problem description and necessary pre-knowledges are described in Section 2. A MTPN-based adaptive constrained stochastic control approach is developed in Section 3. In Section 4, the simulation results of the NSVs attitude motion show the satisfactory flight control performance under the proposed tracking control strategy. Finally, Section 5 gives the conclusions.

where Ω=［α，β，μ］Twith α，β，μ being the angle of sideslip,attack and roll, respectively. ω=［p，q，r］Twith p，q，r being the angular rate of roll, pitch, and yaw, respectively. Fs（Ω）and Ff（Ω，ω）are system state function vectors. y is the output vector. Gs（Ω） and Gf（Ω，ω） are system control matrices.ΔFs=［Δfα，Δfβ，Δfμ］Tand ΔFf=［Δfp，Δfq，Δfr］Tare unknown system uncertainties. Furthermore, the detailed six-degree-offreedom nonlinear flight dynamics are given in Eqs. (2) and(3).Mc=［lc，mc，nc］Tdenotes the vector of the equivalent control input moment, which is generated by the control surface deflections δc=［δe，δa，δr］T. Furthermore, the equivalent moment vector can be described as Mc=Gδδc, where Gδis the control allocation matrix.

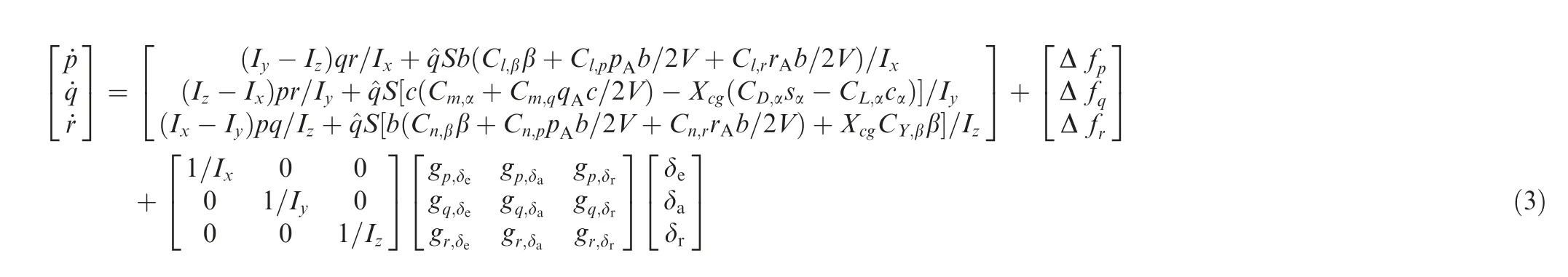
1.1. Notations

The trigonometric functions are simplified as c（·）=cos（·），s（·）=sin（·）, and t（·）=tan（·）. I denotes the identity matrix of the proper dimension. M denotes the mass of the aircraft and V denotes the speed of the aircraft. ^q and S are dynamic pressure and reference area of the wing, respectively. b is the length of wingspan. c is the length of mean aerodynamic chord. g is the gravitational acceleration. Txis the component of thrust T along x direction. Ix, Iy, and Izrepresent the moment of inertia. Xcgis the distance between the focus and the centroid. pA，qA, and rAare the angular rate with respect to the airflow field. CL，α，CY，β，CD，α，Cl，β，Cl，p，Cl，r，Cm，α，Cm，q，Cn，β， Cn，p, and Cn，rare fundamental aerodynamic coefficients.gp，δe，gp，δa，gp，δr，gq，δe，gq，δa，gq，δr，gr，δe，gr，δaand gr，δrare the elements of the control allocation matrix(Their associated details can be found in Ref.8).

2. Problem formulation

Consider the continuous-time nonlinear dynamic model of the NSVs as follows8:

During the design process of NSVs attitude control,the main objective is to design an adaptive controller which can guarantee that the output Ω can track the desired reference signal Ωr. Based on Ωr, the virtual control input ωcof the slow loop subsystem is obtained, and it is always regarded as the desired output signal for the fast loop subsystem. Furthermore, the equivalent control input Mccan be designed via ωc. Owing to Mc=Gδδc,the control command δcof the attitude motion will be obtained by the control allocation process. However,when the attitude control command through servo mechanism and actuator is used to implement the attitude control for NSVs, various stochastic noises exist in the control input channel. The basic control flowchart is shown in Fig. 1.

Consider δcbeing suffered to stochastic disturbances as

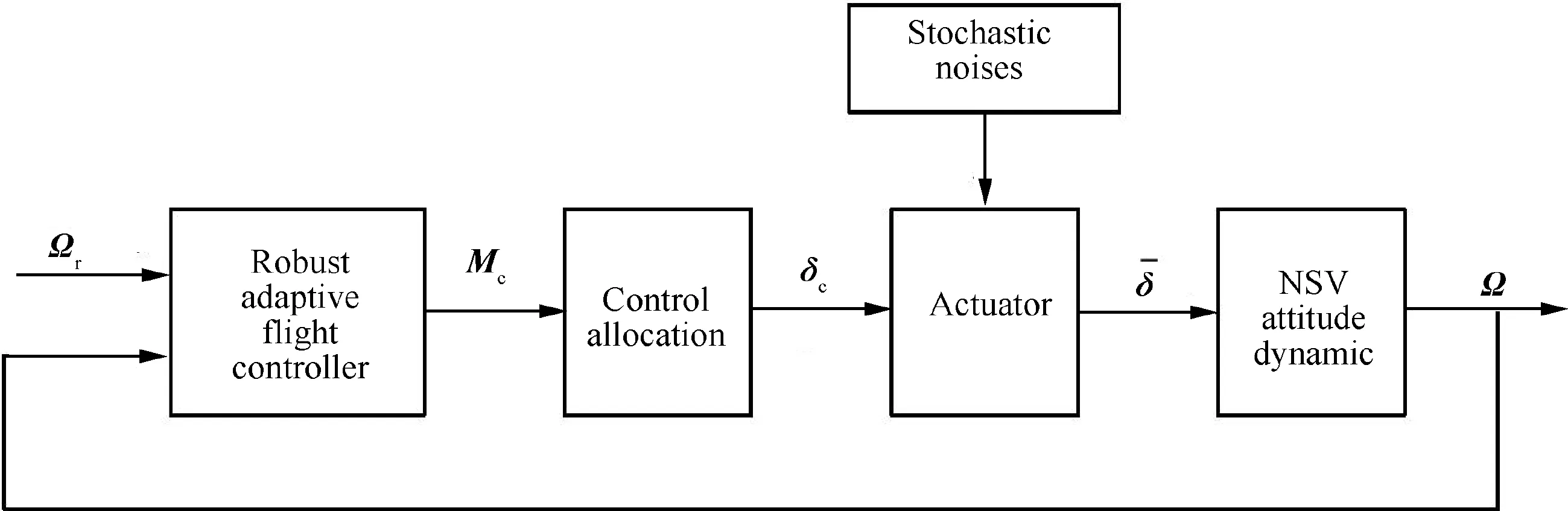
Fig. 1 Control schematic diagram for NSVs.

Furthermore,the attitude dynamic of NSVs with stochastic input disturbances can be rewritten in the following affine nonlinear equations form:

In this paper, by utilizing the error ui-φ（ui） between actual input and saturation input as the system input,the auxiliary system is constructed to tackle the influence of input saturation.

Define

By taking Δ（u）=［Δ1（u1），Δ2（u2），Δ3（u3）］Tas the auxiliary system input, the auxiliary system is constructed as follows35:

where ζsand ζfare the states of the designed auxiliary system.csand cfare the design positive definite matrices.

Remark 1. During the actual flight, the control forces and moments of NSVs are generated by the engine and the control surface deflection. The details of the control input saturation for the NSVs are usually known when the engine and the deflection angle are determined.Therefore,it is reasonable and necessary to consider the input saturation. In addition, to guarantee the controllability of the studied nonlinear stochastic system Eq. (7), it is assumed that Δi（ui） is bounded.Without loss of generality, there exists an unknown positive constant υ*>0 such that ‖Δ（u）‖<υ*.

In this paper, based on MTPN, the designed auxiliary system, and DSC technique, an adaptive attitude tracking stochastic control scheme is presented for the NSVs with stochastic input noise disturbances and input saturation. The attitude control goal is to propose a MTPN-based adaptive constrained stochastic control strategy which can guarantee that the output Ω can track the desired reference signal Ωr.

For ease of the robust stochastic controller design for the NSVs expressed by Eq. (7), some necessary assumptions, definitions and lemmas are needed to be listed as follows:

Assumption 1.26The nonlinear stochastic system Eq. (7) with input saturation and stochastic input noises is input-to-state stable.

Remark 2. Assumption 1 implies that the nonlinear stochastic system Eq.(7)is controllable.For the attitude dynamic model of NSVs subject to input saturation and stochastic input noises, there exists a feasible robust controller u such that the system output Ω can track the desired reference signal Ωr, and the satisfactory attitude tracking control performance can be achieved. Assumption 2 is a standard assumption for flight control scheme design. The invertible requirements is required for controller design, and the boundedness is only required for the stability analysis. In accordance with the features of the DSC, Assumption 3 requires that the desired reference command Ωr=［Ωr1，Ωr2，Ωr3］Tand its time derivatives ˙Ωr， ¨Ωrare assumed to be bounded, which means that the desired trajectory be sufficiently smooth to avoid actuator saturation induced by sudden jumps of tracking error. On the other hand,to obtain the satisfactory attitude tracking control performance under the limited control forces and moments,the bounds of the desired signals can be calculated based on the dynamic of NSVs. Furthermore, in order to handle the stochastic input disturbances, a certain margin always be reserved when the bounds of the desired signals are determined. The reserved margin determines the size range of the stochastic input disturbances that can be suppressed. For Assumption 4, the intensity of stochastic input noise disturbances is assumed to be bounded but the bound is unknown.

Consider stochastic nonlinear system38:

where x denotes the system state, w is a m-dimensional independent standard Wiener process. f（·） and g（·） are locally Lipschitz.

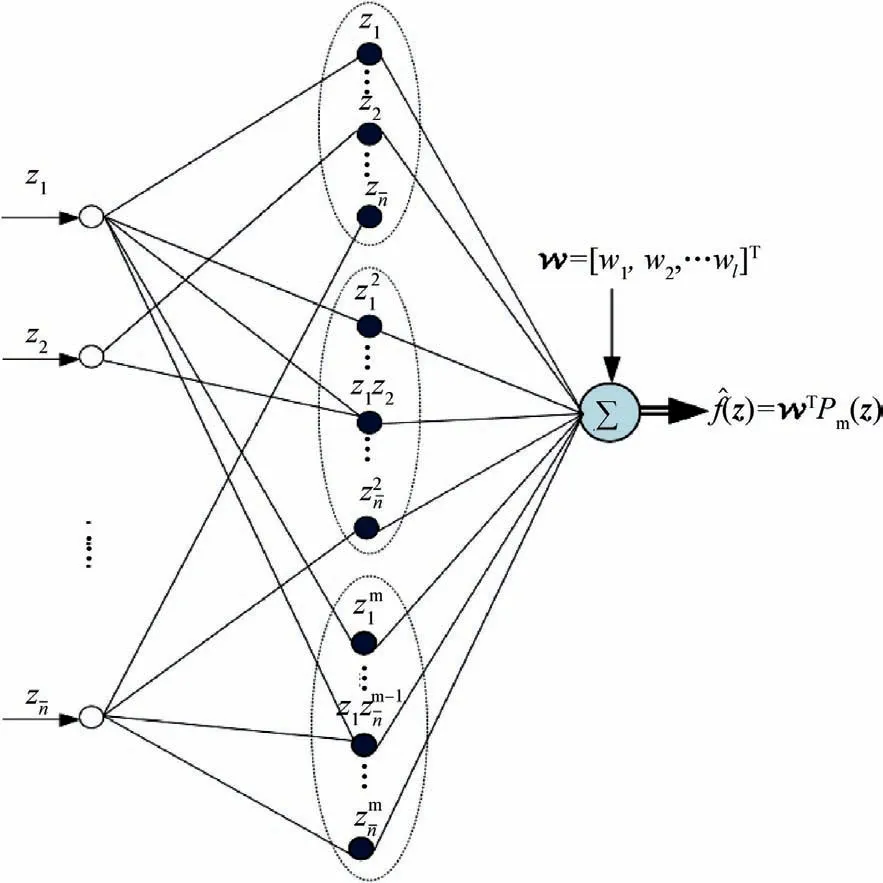
Fig. 2 Topological structure diagram of MTPN.

Definition 1.38For V（x）∈C2（n，+）, define the infinitesimal generator L in the following form:where ni≥0 and nj≥0 satisfy 0 ≤ni+nj≤m with m being the highest power of the monomial in Pm（z）.

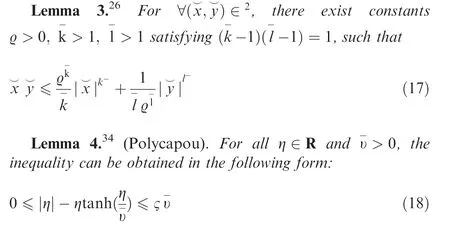
where ς is a constant with ς=e-（ς+1）, i.e. ς=0.2785.

3. MTPN-based adaptive robust stochastic control scheme

In this section, based on MTPN, auxiliary system and DSC technique, a robust stochastic control strategy is presented for the attitude control of NSVs with stochastic input noise and input constraints.

Denote the new error variables as

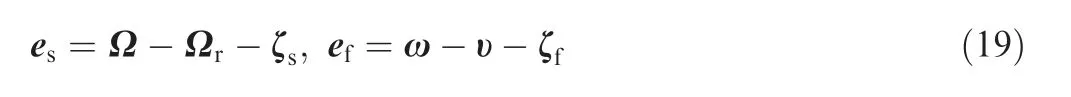
where υ=［υ1，υ2，υ3］T, υj（j=1，2，3） is the output of the firstorder filter being designed.

According to the attitude dynamic of NSVs (7) and (19),the error dynamic is

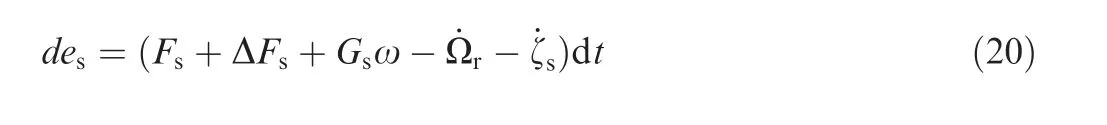
where Γ1>0, λ1>0 and λε1>0 are the design positive definite matrix and positive constants, respectively.

DSC technique will be introduced to avoid repeatedly differentiating ωcin the recursive design. Take the signal ωcas the input of the following first-order filter:

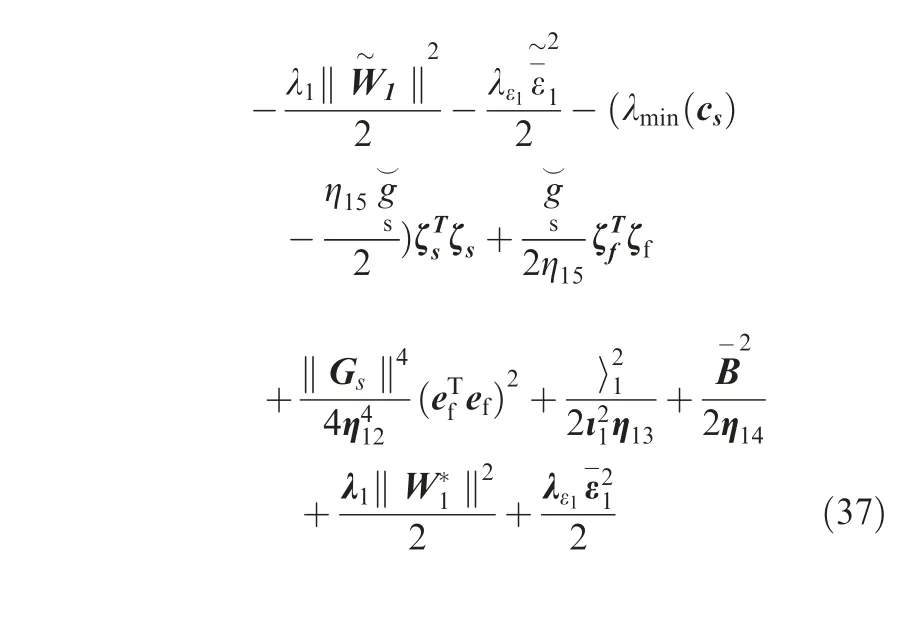
Based on Eq. (19), the dynamic of the variable efis expressed by According to the definition of Frobenius norm, the norm compatibility, and basic inequality, we have

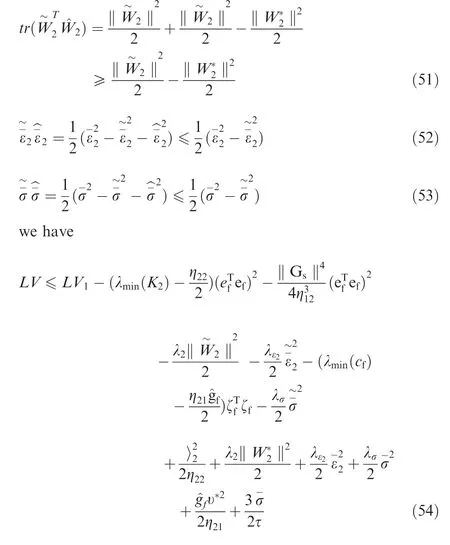
Combining with Eq. (37), we have

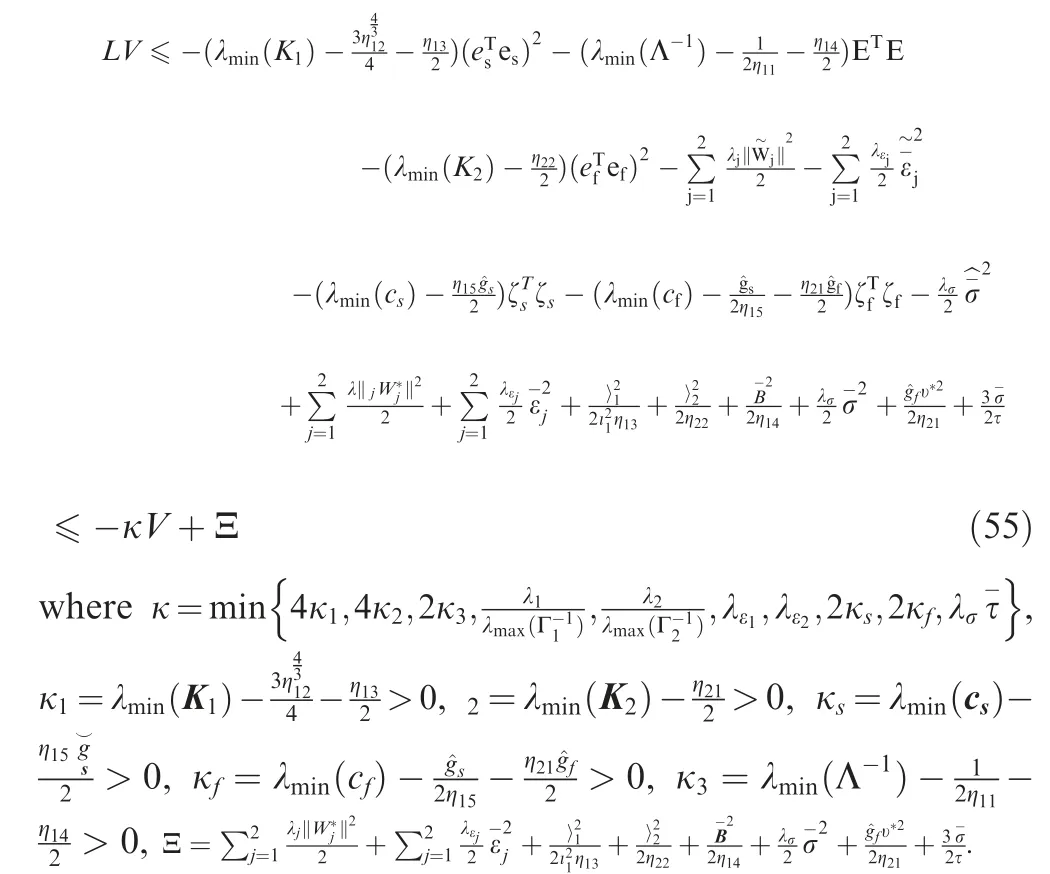
Now,the complete design procedure of the robust stochastic control scheme can be concluded as the theorem in the following form.

Theorem 1. Consider the NSVs attitude control system Eq. (7)with saturation nonlinearities and stochastic input noise disturbances satisfying Assumptions 1–4,then under the MTPN-based robust stochastic attitude tracking controller consisting of Eqs.(23)–(25), and Eqs. (41)–(44), all the closed-loop signals are SGUUB in probability. Additionally, by selecting appropriate parameters, the tracking errors will converge to a small neighborhood with a tunable radius.

Proof. By choosing the Lyapunov function as Eq. (45), and according to Eq. (55), that is

Then, one has

Furthermore, we have

Thus,

And then, it yields

Therefore,according to the definition of Vand Eq.(60),we know that all signals of the entire NSVs attitude motion system are SGUUB in the sense of probability. In special, the tracking errors are SGUUB in fourth moment.

It is apparent that the satisfactory flight control effect can be achieved by selecting the appropriate design parameters.

Remark 4. To fully consider the effect of input saturation, an auxiliary system Eq. (10) is constructed and the auxiliary system signals ζsand ζfwill be used to design the virtual control law ωcand the attitude tracking robust stochastic controller u,respectively.On the other hand,the boundedness in probability of all the closed-loop system signals is rigorous proven under the proposed robust stochastic control scheme.Furthermore, the boundedness of the tracking errors is equivalent to the boundedness of the new error variables esand efdefined by Eq. (19).

4. Simulation results

To verify the control effect under the proposed MTPN-based adaptive constrained control strategy, the numerical simulation results of the NSVs attitude motion is implemented. The detailed expression of the aerodynamic parameters of the NSVs can be found in Ref.8, the actual control inputs of the attitude dynamic of the NSVs are three control surface deflection angles δe， δa，and δr.It is assumed that aerodynamic coefficients have ±20% uncertainties and there exist stochastic input noises σiξi（i=1，2，3）acting on the fast-loop subsystem,that is

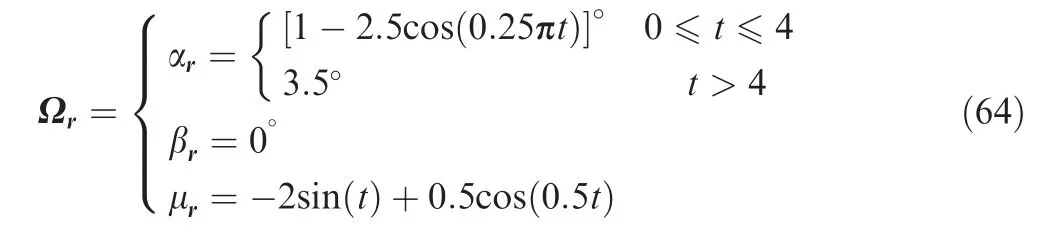
The desired reference signal is given by ι1=ι2=10， Γ1=Γ2=I3， b1=b2=10， η11=10， η12=1，τ=20， τ-=1， λ1=λ2=λε1=λε2=λσ=0.1，and Λ=diag｛0.1，0.1，0.1｝.

The numerical simulation results for the attitude motion of the NSVs are obtained as shown in Figs. 4–8. Figs. 4–6 show

By choosing the parameters σ1， σ2and σ3, the control surface deflection angles have stochastic uncertainties with sufficiently large probability. In the process of simulation, the noise density parameters are set as σ1=σ2=σ3=0.05,V0=3000 m/s and H=22 km. The initial values of the system states are selected as α0=1◦， β0=1◦， μ0=-1◦，p0=0 rad/s， q0=0 rad/s， and r0=0rad/s. The saturationinputlevelofφ（M）aresetas φmax（Mc）=［2000，20000，20000］TKN·m. To compensate for the influence of saturation nonlinearities, the auxiliary system is designed as Eq. (11) with cs=diag｛20，20，20｝ and cf=diag｛50，50，50｝. In this simulation, by selecting certain parameter values, stochastic input moment disturbances are shown in Fig. 3.

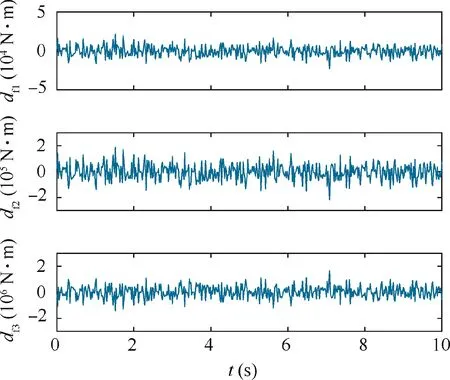
Fig. 3 Stochastic moment disturbance df =［df1，df2，df3］T.

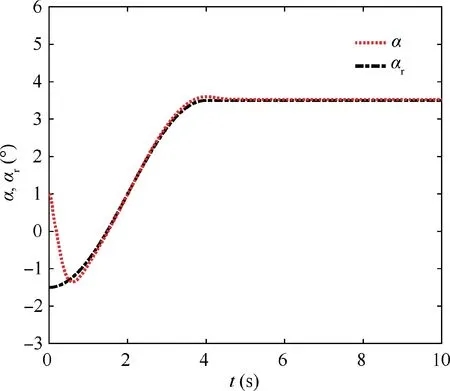
Fig. 4 Tracking response result of angle of attack α.

Fig. 5 Tracking response result of angle of sideslip β.

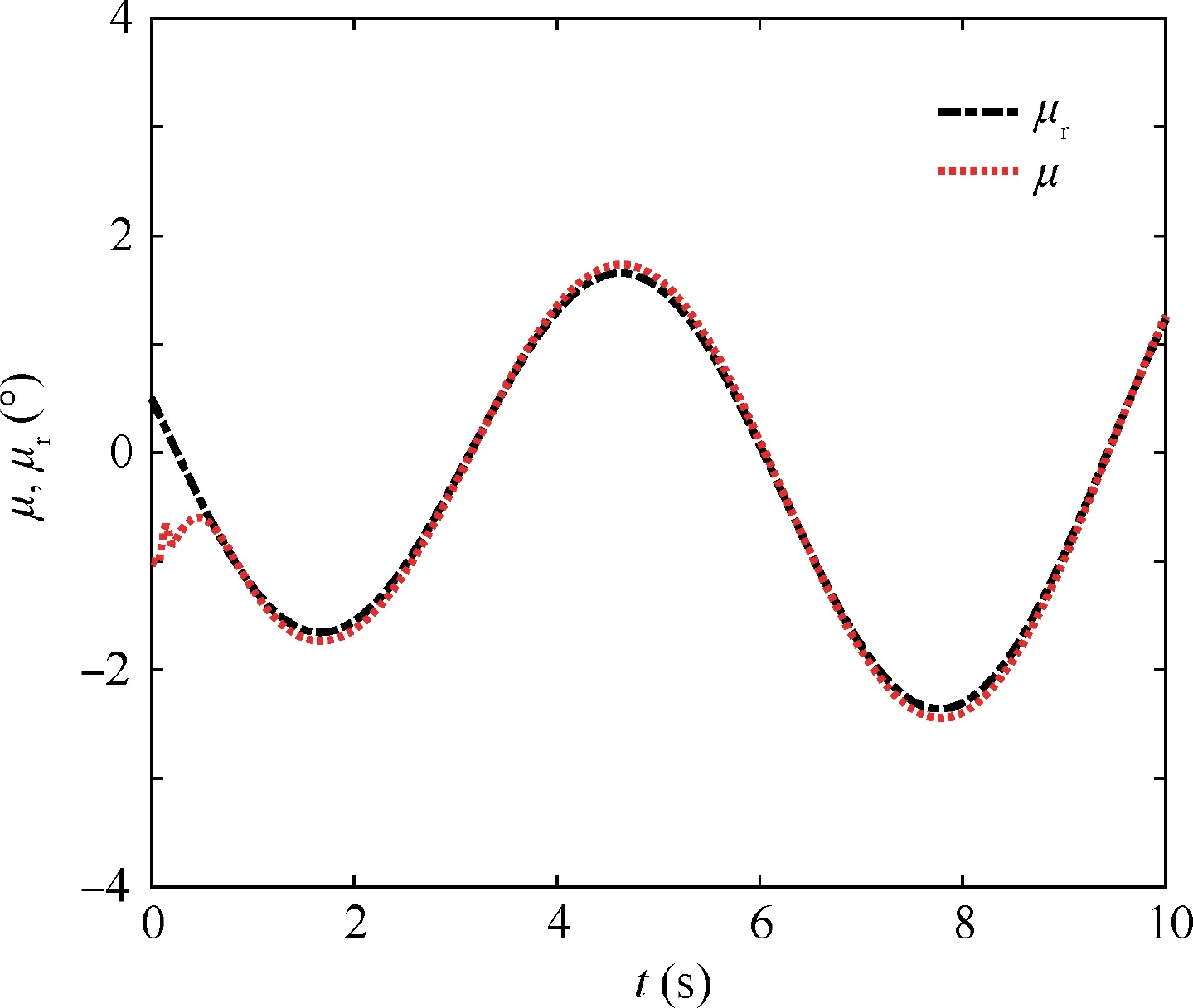
Fig. 6 Tracking response result of angle of roll μ.

Fig. 7 Tracking errors eα，eβ and eμ of attitude angles.

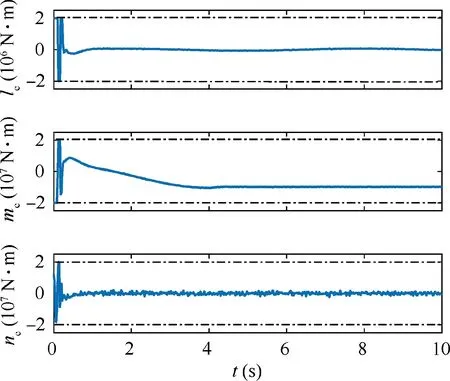
Fig. 8 Saturation control inputs.

The virtual control signal, adaptive attitude tracking controller, and adaptive update laws are designed as Eqs. (24)–(26) and (41)–(44). The designed control parameters are selected as K1=diag｛5，5，5｝， K2=diag｛110，120，160｝,the tracking response results of the attitude angle.It is easy to see that the satisfactory attitude tracking effect for the NSVs with stochastic input noise disturbances is achieved under the proposed robust stochastic controller. Meanwhile, the small tracking errors eα， eβand eμof the attitude angles for the NSVs attitude control are shown in Fig. 7. Additional,Fig. 8 displays the saturation control input of the NSVs. It can be inferred that the influence of input saturation is compensated by the designed auxiliary system.

5. Conclusions

In this paper, consider the stochastic input noise disturbances existing in the attitude control system of NSVs, a novel attitude motion dynamic of the NSVs is modeled as the MIMO stochastic nonlinear system. Then, the MTPN is introduced to approximate the unknown functions, and an auxiliary system is adopted to compensate the influence of input saturation.Furthermore, based on MTPN, auxiliary system, and DSC technique,a robust adaptive stochastic control strategy is proposed for the NSVs attitude control system subjected to input constraints and stochastic input noise. Stochastic Lyapunov stability theory is utilized to analysis the stability in the sense of probability of the entire closed-loop system. Finally, the numerical simulation results of the NSVs attitude motion show the satisfactory flight control performance under the proposed tracking control strategy.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was co-supported by the National Natural Science Foundation of China (Nos. 61825302, 61903118), the Natural Science Foundation of Anhui Province of China (No.1908085QF290), the Research Development Fund of Hefei University of China (No. 18ZR11ZDA), and the Major Science and Technology Project of Anhui Province of China(No. 18030901009).