A hybrid multidimensional Riemann solver to couple self-similar method with MULTV method for complex flows
Feng QU, Di SUN, Junjie FU, Junqiang BAI
School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China
KEYWORDS Complex flows;Computational fluid dynamics;Multidimensional;Riemann solver;Self-similar
Abstract Since proposed, the self-similarity variables based genuinely multidimensional Riemann solver is attracting more attentions due to its high resolution in multidimensional complex flows.However,it needs numerous logical operations in supersonic cases,which limit the method’s applicability in engineering problems greatly. In order to overcome this defect, a hybrid multidimensional Riemann solver, called HMTHS (Hybrid of MulTv and multidimensional HLL scheme based on Self-similar structures),is proposed.It simulates the strongly interacting zone by adopting the MHLLES (Multidimensional Harten-Lax-van Leer-Eifeldt scheme based on Self-similar structures)scheme at subsonic speeds,which is with a high resolution by considering the second moment in the similarity variables. Also, it adopts the MULTV (Multidimensional Toro and Vasquez)scheme, which is with a high resolution in capturing discontinuities, to simulate the flux at supersonic speeds. Systematic numerical experiments, including both one-dimensional cases and twodimensional cases, are conducted. One-dimensional moving contact discontinuity case and sod shock tube case suggest that HMTHS can accurately capture one-dimensional expansion waves,shock waves, and linear contact discontinuities. Two-dimensional cases, such as the double Mach reflection case, the supersonic shock / boundary layer interaction case, the hypersonic flow over the cylinder case, and the hypersonic viscous flow over the double-ellipsoid case, indicate that the HMTHS scheme is with a high resolution in simulating multidimensional complex flows.Therefore, it is promising to be widely applied in both scholar and engineering areas.
1. Introduction
In the last decade, with the rapid development of aerospace science, the aerodynamic design technology of the aircraft has witnessed a huge success and the flight envelops of the vehicles are becoming wider. However, it still remains an appealing issue to pursue the wider flight envelop, which makes it in a higher demand for the accuracy in predicting the aerodynamic loads1.
In general,the widely used technologies to predict the aerodynamic loads are the engineering experienced estimation methods,2the wind tunnel experimental methods,3and the Computational Fluid Dynamics (CFD) methods.4,5Among these technologies, the engineering experienced estimation methods are based on simple theory and cannot be applied to complex flows. The wind tunnel experimental methods improve the engineering experienced estimation methods’drawbacks. However, they are incapable of reproducing real flight environment due to the scale limitation of the wind tunnel.In comparison,the CFD technology is capable of conducting simulations covering the whole flight range of the airliners and avoiding the scale limitation of the wind tunnel. Moreover, it can be conveniently applied to simulate threedimensional complex flows accurately. Therefore, studies on the CFD technologies are attracting more attentions.6,7
Nowadays, most commercial CFD software and in-house CFD codes, such as FLUENT,8CFDX,9CFL3D,10OVERFLOW,11FUN3D,12etc.,have been widely used to predict the aerodynamic loads of the vehicles. However, systematic analyses indicate that all these codes’ accuracy in simulating multidimensional complex flows cannot satisfy the engineers’ demands.13In theory, all these software and codes are developed based on the traditional direction splitting procedure,in which the multidimensional governing equations are solved direction by direction and the influences among different directions are ignored.14In order to dispel such defect,scholars proposed the concept of the genuinely multidimensional Riemann solvers.15These solvers consider not only the waves transporting normal to the cell interfaces,but also those transverse to the cell interfaces. Therefore, they improve the existing direction splitting methods’ accuracy in simulating multidimensional complex flows theoretically.16–23However,all these methods are not widely used in the aerospace science,because they are constructed in complex forms which are difficult to be implemented.24
Recently,to make the genuinely multidimensional Riemann solvers easy to be implemented,Balsara proposed a novel multidimensional wave mode. Taking two-dimensional case as an example, such model assumes that four states interact with each other simultaneously, and a constant state appears in the interacting zone. With such simple wave model, Balsara proposed the genuinely multidimensional HLLE Riemann solver with a simple closed form in both two-dimensional case and three-dimensional case.25,26Similar studies were also conducted by Vides et al.27Later, Balsara improved the multidimensional wave model by introducing sub-structures to the interacting zone to be capable of capturing contact discontinuities accurately.28On the other hand, to avoid the complex mathematical operations in specifying the directions of the contact discontinuities, Mandal and Sharma proposed a genuinely multidimensional Riemann solver based on the flux splitting procedure.29By adopting the Toro splitting procedure to split the inviscid flux into the convective flux and the pressure flux and controlling the numerical dissipation in the pressure flux, this method can capture contact discontinuities accurately. Inspired by Mandal’s work, Qu et al. adopted the Zha-Bilgen splitting procedure to split the inviscid flux and proposed the ME-AUMSMPW scheme.30Also, to make the flux splitting multidimensional Riemann solver applied to engineering problems, Qu et al. extended Balsara’s twodimensional wave model to the curvilinear coordinates and proposed a new genuinely multidimensional Riemann solver for complex flows.31
In theory, all flow structures, such as the shocks, the rarefaction waves, and the linear contact discontinuities which are depicted by the Euler equations, satisfy the self-similar property.Moreover,studies by Collins and Glaz indicated that the strongly interacting state in multiple dimensions evolve similarly.32However, the wave model proposed by Balsara does not take the self-similarity of the governing equations into accounts and only fits sub-structures into the HLL resolved state. For these,all those genuinely multidimensional Riemann solvers based on such wave model cannot capture high order moments in interacting states in complex flows.Following this conclusion,Balsara improved his multidimensional wave model in self-similarity variables.33,34Results indicate that this new wave model can improve the accuracy in simulating the interacting zone.However,this work cannot be used in engineering areas because it is built on the Cartesian coordinates. In addition, it needs large logical operations in cases where the strongly interacting state is flowing supersonically.35Therefore, it is necessary to devise a multidimensional Riemann solver, which is based upon the self-similar variable in curvilinear coordinates and can avoid logical operations in identifying the supersonic cases.
This study is organized as follows.In Section 2,the governing equations for fluid flows in similarity variables will be overviewed briefly. Section 3 will introduce the construction of a novel self-similar structures based genuinely multidimensional Riemann solver, called HMTHS (Hybrid of MULTV and Multidimensional HLL-type schemes based on Self-similar structures). Several numerical tests are carried out and will be presented in Section 4. The conclusions will be drawn in Section 5.
2. Governing equations
2.1. Navier-Stokes equations
In general, the Navier-Stokes (NS) equations are used to describe the motions of viscous flows. In two-dimensional curvilinear coordinates, they can be written in the following form:
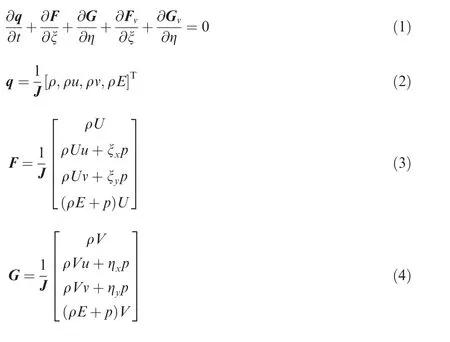
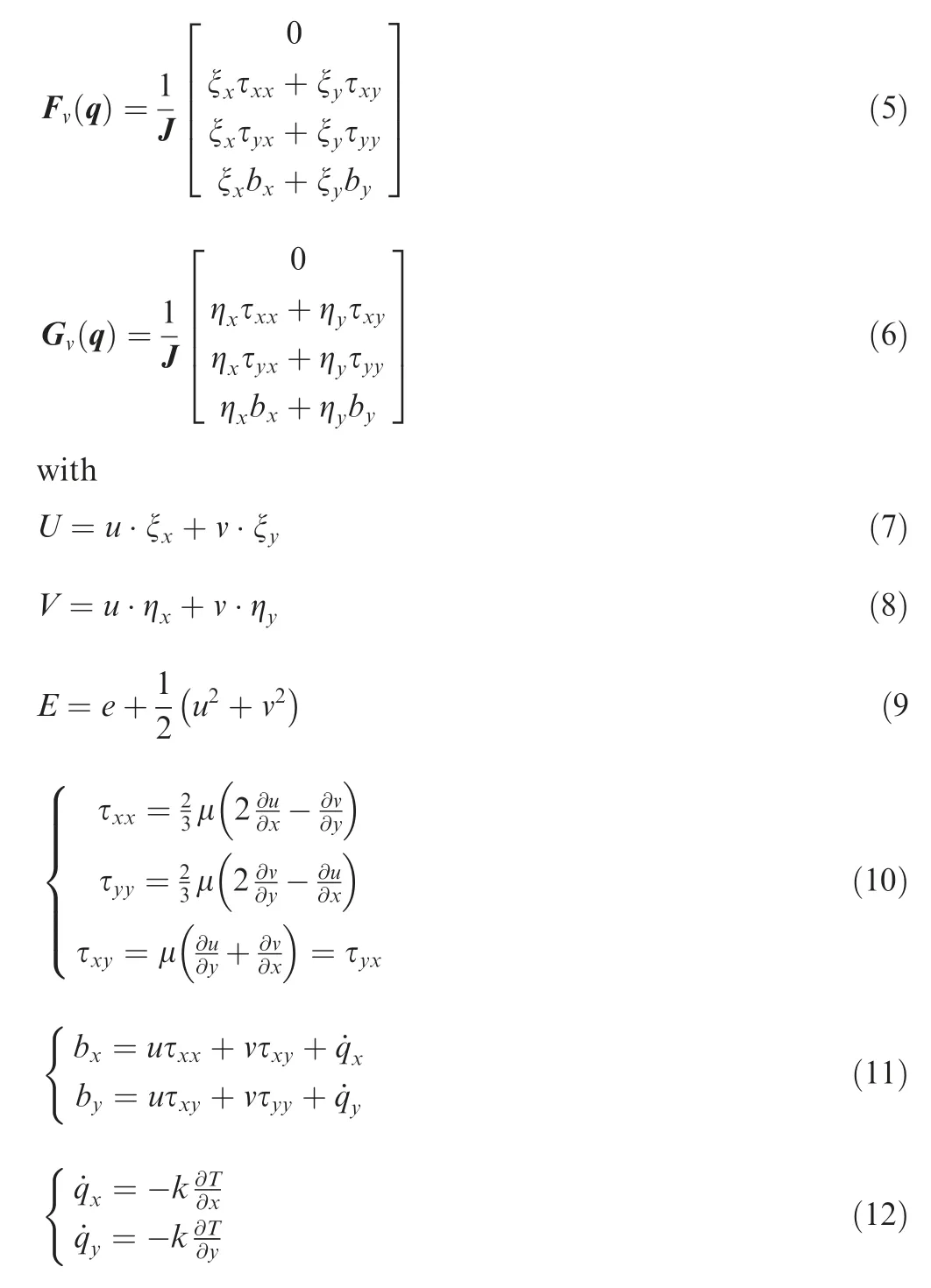
where ρ is density,u and v are velocity vector components,p is static pressure,μ is the static viscosity coefficient,k is the coefficient of the thermal conductivity, e is internal energy,ξx,ξy,ηx,ηyare the metric coefficients, and J indicates the transformation Jacobian matrix of the coordinate. More details can be found in Ref. [13].
2.2. Euler equations
According to theoretical analyses of the NS equations’mathematical property, scholars found that the viscous terms in Eq.(1) satisfy the ellipse property while the inviscid terms satisfy the hyperbolic property.14Also, the partial difference equations with the ellipse property can be well resolved by adopting the central methods. Therefore, most studies are conducted to construct numerical methods to numerically solve the Euler equations. In two-dimensional case, the Euler equations can be written as follows:

2.3. Multidimensional Euler equations in similarity variables in curvilinear coordinates
With self-similarity variables, the Euler equations in curvilinear coordinates are written as follows:

3. Construction of HMTHS schemes
3.1. Finite volume strategy for genuinely multidimensional Riemann solver
Nowadays, most scholars adopt the finite volume methods to numerically solve the governing equations which depict the motions of fluid flows.In two-dimensional case,it can be written as follows:

where the symbols i and j indicate the indices along the ξ direction and the η direction as shown in Fig.1.27Also,the symbols LU, LD, RU, and RD indicate the four different initial states at the left-up, left-down, right-up, and right- down states.
As can be seen in Eq. (17), the traditional finite volume technology is based on the direction splitting procedure. It ignores the interactions of waves at different directions and only considers the waves traveling orthogonal to the cell interfaces. In order to dispel this defect, Balsara proposed a novel finite volume method with the following form25:


Fig. 1 Two-dimensional computational mesh.27
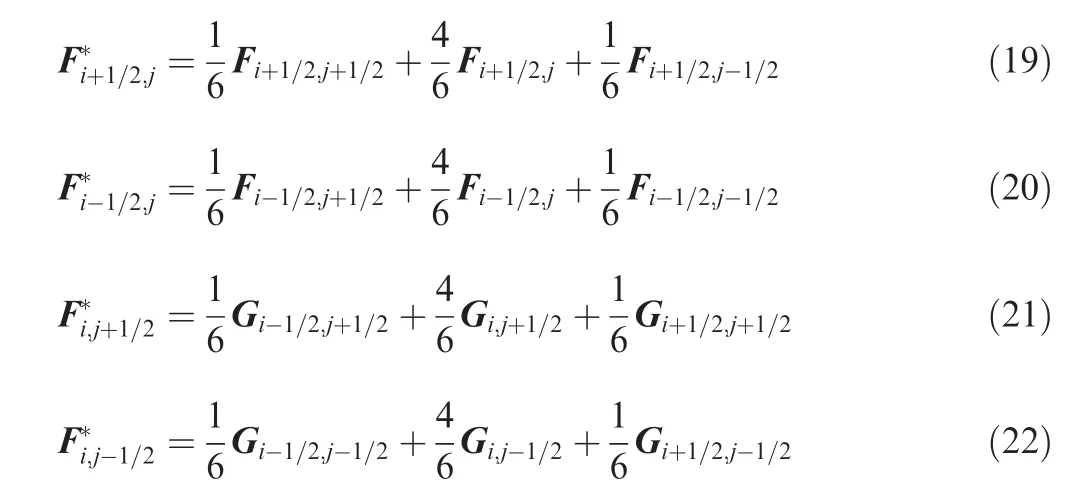
By adopting the flux at the vertex of the computational mesh such as the grid point labeled (i+1/2, j+1/2) as in Fig. 1, this procedure is capable of considering the waves at different directions.
3.2. Multidimensional wave model for genuinely multidimensional Riemann solver
Fig. 2 shows the two-dimensional wave model which Balsara proposed.In this model,there are four different states interacting at the vertex of the computation mesh. Taking the corner point label (i+1/2, j+1/2) as an example, these four initial states are called LU, LD, RU, and RD, and the interacting zone (S. I. State) is with the boundary determined by the fastest‘left’,‘right’,‘up’,and‘down’moving waves’speeds SL,SR,SU, and SD. The definitions of these speeds can be found in Ref. 31.
3.3. Multidimensional Riemann problem in similarity variables
Due to the self-similar property of the conservative Euler equaitons, Eq. (17) which describes the interacting zone can be set up with different moments in the similarity variables.Among these moments, the zeroth moments correspond to the resolved states, and the first moments correspond to the first-order gradients of the resolved states. Similarly, higher order moments correspond to higher order gradients of the resolved states. In Ref. 32, Collins and his co-workers found that the resolved states are assocaited with the contact discontinuitiy, which indicates the first-order gradients of the resolved density. Therefore, the sub-structures in the interacting zone will be imparted with a general basis set of selfsimilarity variables by considering the first moments in this study.
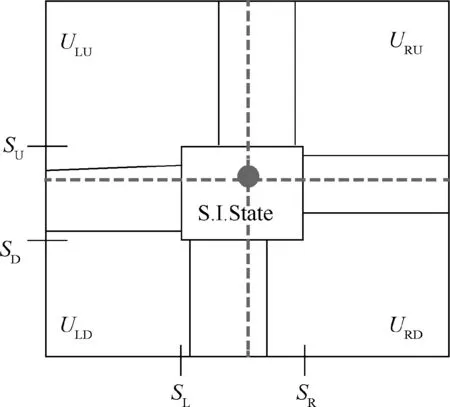
Fig. 2 Wave model for two–dimensional Riemann problem.33
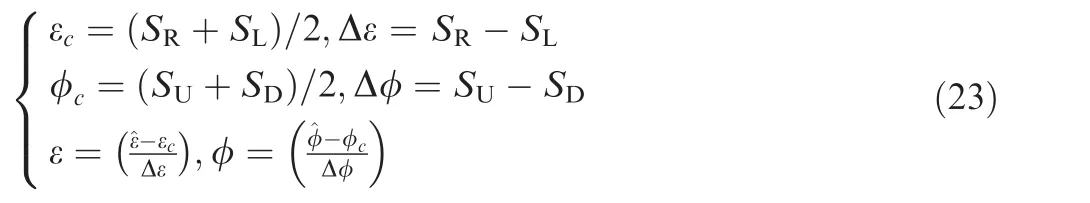
As a first step, coordinate transformations in the similarity variables are conducted as follows for simplicity:By adopting the Hermite basis set of self-similarity variables with the first moments, the conservative variable vectors and the flux vectors are expanded as
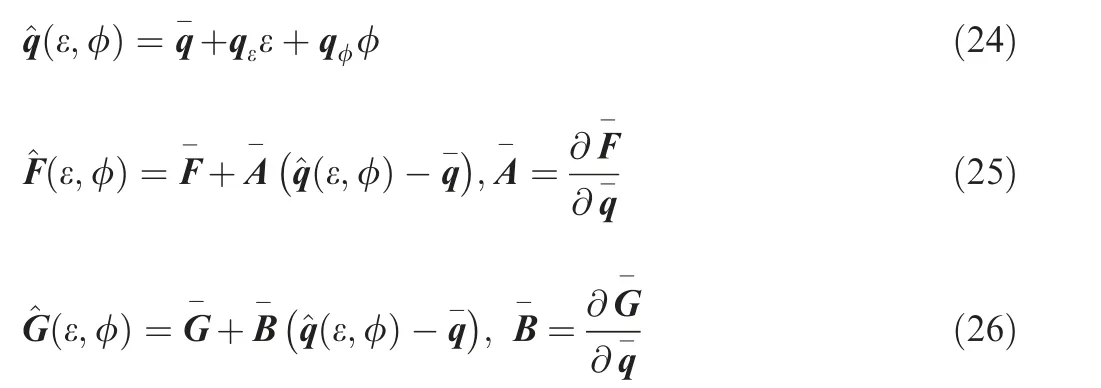
With these definitions aforementioned, the multidimensional compressible Euler equations in Eq. (18) become
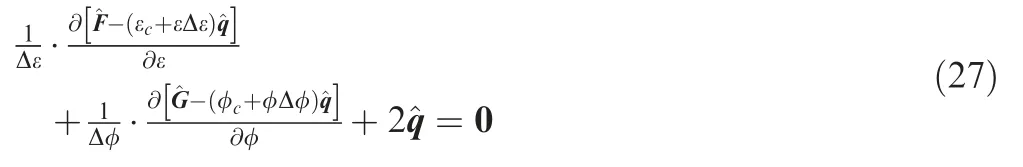
Following Balsara’s idea, the Galerkin projection technology is used to solve the governing equations in Eq. (27). In other words, a test function Φ (ε,φ ) is employed to multiply Eq. (27) as follows:
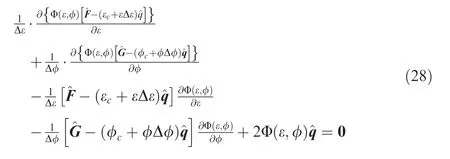
3.4. Calculation of flux vectors
3.4.1. Calculation of flux vectors at corner points in subsonic cases
With the conservative variable vectors and the flux vectors expanded with the Hermite basis set of self-similarity variables as in Eqs. (24)–(26), the conservative vectors at the corner labeled(i+1/2,j+1/2)can be obtained by adopting the test function Φ( ε,φ )=1 and being integrated over the entire wave model shown in Fig. 2:
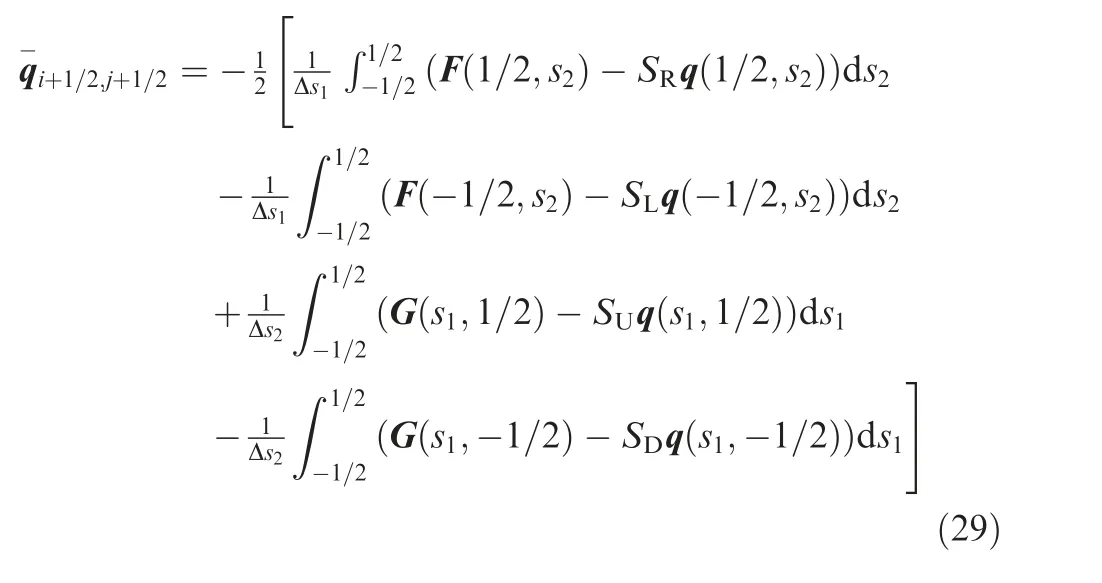
Similarly, by integrating such equations over the entire wave model as in Fig. 2 with the test functions Φ(ε,φ )=εandΦ(ε,φ )=φ, the flux vectors in the ξ direction and the η direction at the corner labeled (i+1/2, j+1/2)are obtained as follows:

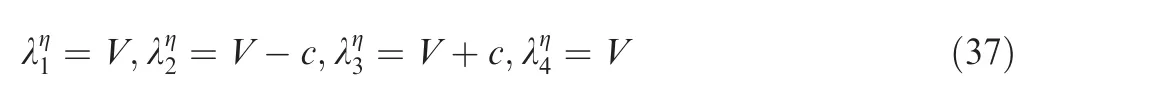
where c indicates the speed of sound.
3.4.2. Calculation of flux vectors at corner points in supersonic cases
In supersonic cases, the interacting state will not overlie the vertex as shown in Fig. 2. Therefore, the fluxes at the corner points could not be obtained by adopting the methods in Section 3.4.1. For these, Balsara proposed a method to simulate the flux vectors based upon the upwind property of the Euler equations. This method can be presented as
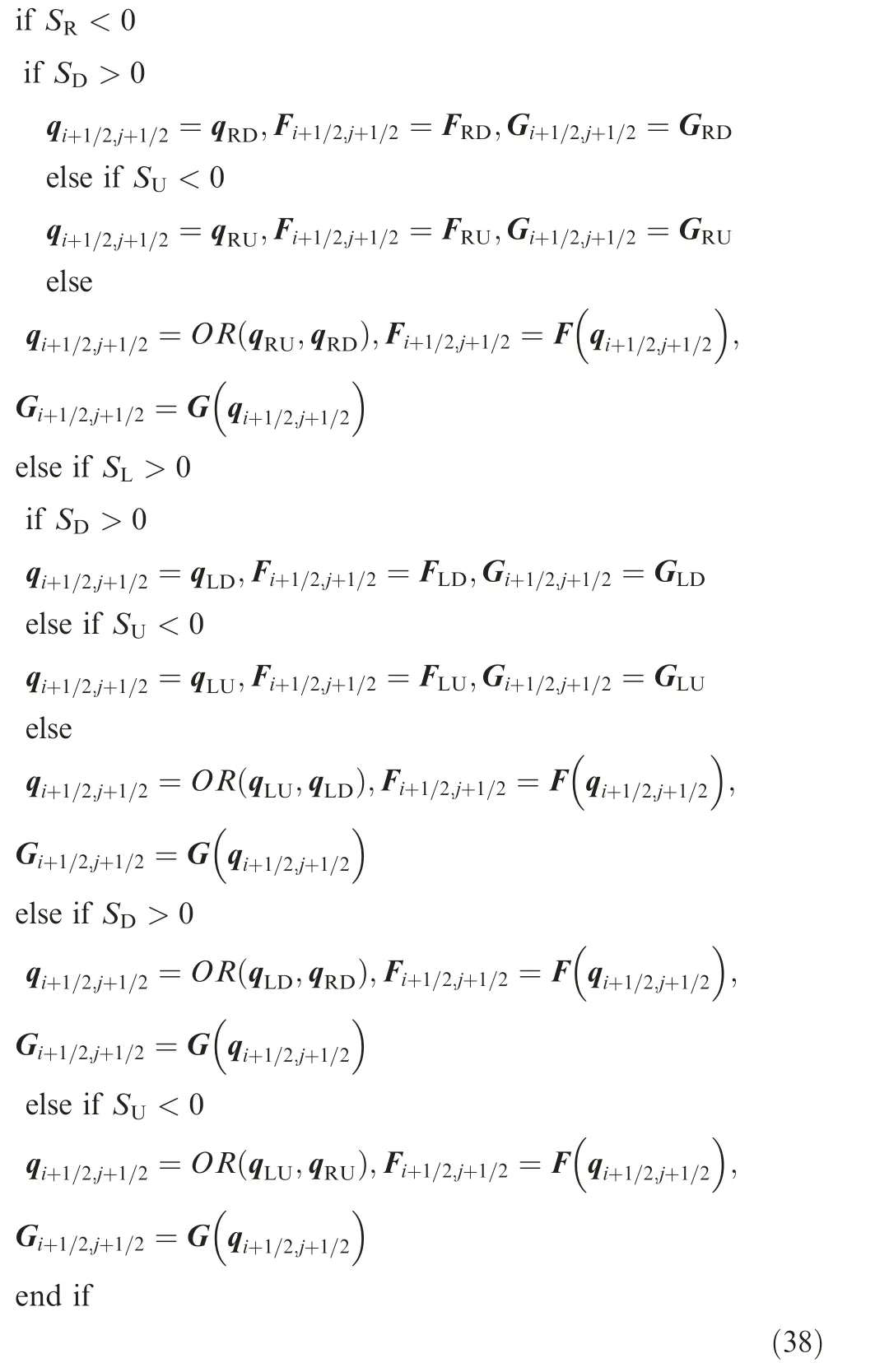
where the subroutine OR indicates that the flow variables at the corner point will be obtained by solving the corresponding one-dimensional Riemann problem.

3.4.3. Calculation of fluxes at the midpoints of cell interfaces
Taking the flux Fi+1/2,jin Eq.(18)as an example,it is simulated in this study by adopting the HLLEM scheme, which is based upon the three-wave model to accurately capture the linear degenerate fields. In two-dimensional cases, it is with the following forms36,15:


Fig. 3 Schemes’ density distributions in one-dimensional cases.

where ~means the Roe average, andare the speeds of the right going and left going waves respectively.
4. Numerical tests
4.1. One-dimensional cases


Fig. 4 Density contours of double-Mach reflection at t=0.2.

Fig. 5 Computational mesh for supersonic shock/boundary layer interaction.
4.2. Two-dimensional double Mach reflection of a strong shock
In this case,the computational domain is [0,4 ]× [0,1 ]with the initial conditions and the boundary conditions defined in Ref.38.For the spatial accuracy and the temporal advancement,the first-order reconstruction method and the third-order Runge-Kutta method with the total variation diminishing property were adopted.
Fig.4 displays the schemes’density contours at t=0.2.All these figures are based on the same contour levels. As can be clearly seen, HMTHS is robust against the shock anomaly near strong shocks.39Also, it can capture flow structures such as the reflection shock and the shear waves more accurately than HLLC by considering the self-similarity property of the interacting zone in multidimensional Riemann problems.
4.3. Supersonic shock/boundary layer interaction
In this case, two-dimensional shock/boundary layer interaction problem induced by a shock impingement on the wall is studied.For the initial conditions, the free stream Mach number is 2, the free stream Reynolds number is 2.96×105, and the impinging angle of the shock is 32.598°. The computation model and the computational mesh are shown in Fig. 5. It should be reminded that the number of grids adopted in this case is 219(wall normal)×172(flow direction).Also,the cells were clustered near the wall to capture the boundary layer accurately. For time integration, the implicit LU-SGS method40was employed to carry out the simulation for 20,000 steps to achieve six orders’ reduction of the residual at least.For spatial accuracy,the second-order SDWLS reconstruction technology was used.41
Fig. 6 displays the density contours obtained by the HMTHS scheme. It accurately captures the shock, the reflected shock, the separation zone, the expansion wave,and the attached shock.Fig.7 shows the skin friction distribution which HMTHS obtained and compared it with the widely used Roe scheme, the HLLC scheme and the experimental data.42As can be seen, HMTHS accords with experimental data much better than the traditional one-dimensional Riemann solvers.
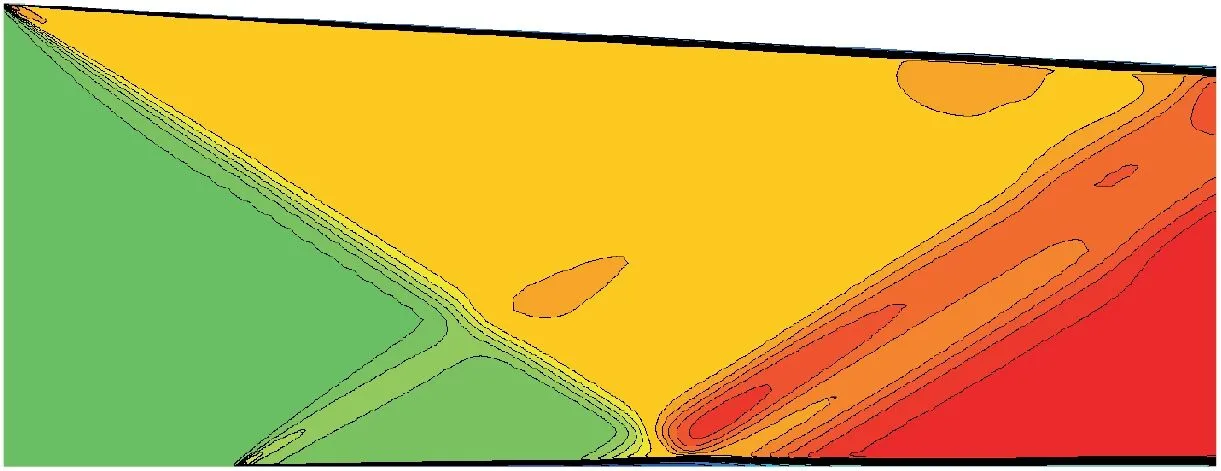
Fig. 6 Mach contours for supersonic shock/boundary layer interaction.
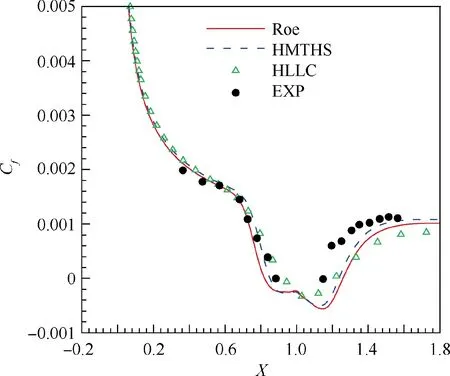
Fig. 7 Schemes’ skin friction distributions.
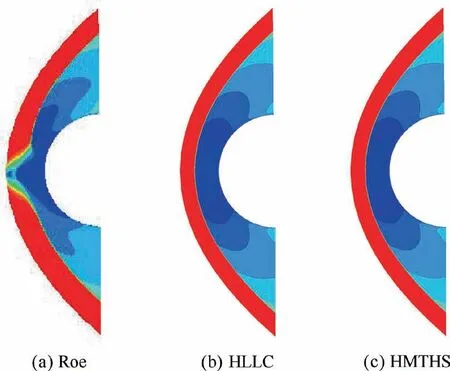
Fig. 8 Schemes’ Mach number contours of hypersonic viscous flow over blunt body.
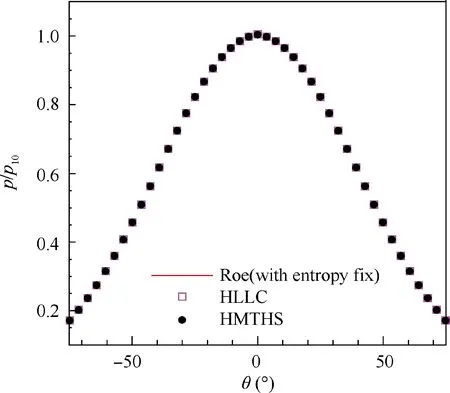
Fig. 9 Schemes’ surface pressure distributions (θ indicates the center angle at different locations).
4.4. Hypersonic flow over the cylinder
In order to display the HMTHS scheme’s performance at hypersonic speeds, the two-dimensional hypersonic flow over the cylinder with the freestream Mach number 8.1 is studied.For spatial accuracy, the first-order reconstruction method was used.Moreover,all computations were advanced for more than 20,000 steps by adopting the LUSGS technology to achieve eight orders’ reduction of the residual.
Schemes’ pressure contours illustrated in Fig. 8 indicate that HMTHS is robust against the shock anomaly, which accords with the conclusion in the double Mach reflection case.Also,the pressure distributions in Fig.9 suggest that HMTHS is with a high resolution in capturing hypersonic flows. It should be reminded that the pressure distribution obtained by the Roe scheme is simulated by combining Roe with the entropy fix.43
4.5. Hypersonic viscous flow over a two-dimensional doubleellipsoid
In this test case,two-dimensional hypersonic viscous flow flowing past the double-ellipsoid with the free stream Mach number 8.15 is studied. In addition to the free stream Mach number, the free stream pressure is 370.7 Pa, the free stream temperature is 56 K, the unit Reynolds number is Re∞/m=7.68×106, and the temperature of the wall is with the constant value of 288 K. Details about the model and experimental analyses of such case can be found in Ref.44.
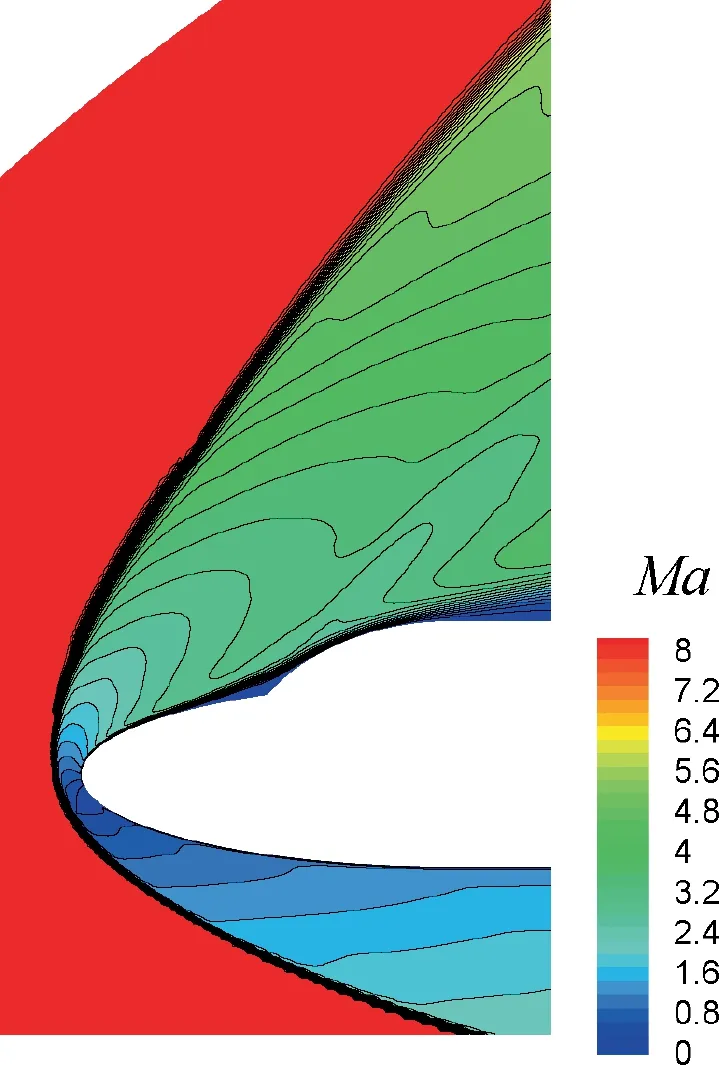
Fig. 11 HMTHS scheme’s Mach number contours for hypersonic viscous flow over a two-dimensional double-ellipsoid case.
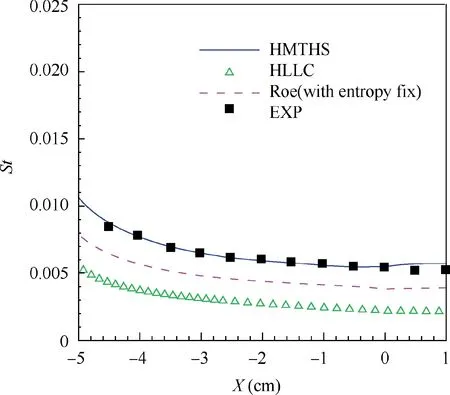
Fig. 12 Distributions of schemes’ Stanton numbers along the meridians of windward side.
Fig. 10 shows the computational mesh adopted in this study.The grids are clustered near the wall in the normal direction to make the cell Reynolds number equal to 2 to guarantee the accuracy in capturing boundary layers.45Also, the grids are clustered at the corner in the flow direction due to the possible drastic changes of the flow variables.
For spatial accuracy,the first-order reconstruction technology was used and the SST RANS model was adopted to simulate the turbulence eddy viscosity.46For time integration, all simulations are conducted for more than 30,000 steps with the LUSGS method to guarantee six orders’ drop of residual.
Fig. 11 displays the Mach number contours by HMTHS.Obviously, it accurately captures bow shock at the head of the ellipsoid, the expansion waves, the separation zone, and so on. It suggests that the HMTHS scheme proposed in this study is with a high resolution in capturing multidimensional complex flow structures.
Fig. 12 compares the schemes’ distributions of Stanton numbers along the windward side. As can be seen, HMTHS accords with the experimental data much better than the traditional one-dimensional Riemann solvers.
5. Conclusions
In this study,a hybrid multidimensional Riemann solver called HMTHS is proposed. At subsonic speeds, it constructs the strongly interacting zone by adopting the MHLLES scheme.In supersonic cases, the fluxes will be obtained by employing the MULTV scheme. Several one-dimensional and twodimensional cases are carried out. The one-dimensional moving contact discontinuity case and sod shock tube case in Section 4.1 indicate that the HMTHS scheme proposed in this study is with a high resolution in simulating one-dimensional expansion waves, shock waves, and linear contact discontinuities.The two-dimensional supersonic/hypersonic cases in Sections 4.2–4.5 demonstrate that the HMTHS scheme is with a high level of accuracy at supersonic/hypersonic speeds.Also,it can simulate complex subsonic interacting flows,such as the separation zone and the boundary layer, accurately.
All in all,it is promising to be further studied and applied in both academic and engineering areas.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This study was co-supported by National Natural Science Foundation of China (Nos. 11902265 and 11972308), Natural Science Foundation of Shaanxi Province of China (No.2019JQ-376), and the Fundamental Research Funds for the Central Universities of China (Nos. G2018KY0304 and G2018KY0308).
 CHINESE JOURNAL OF AERONAUTICS2021年7期
CHINESE JOURNAL OF AERONAUTICS2021年7期
- CHINESE JOURNAL OF AERONAUTICS的其它文章
- Integrated batteries layout and structural topology optimization for a solar-powered drone
- Polynomial networks based adaptive attitude tracking control for NSVs with input constraints and stochastic noises
- Morphing wing flaps for large civil aircraft:Evolution of a smart technology across the Clean Sky program
- Review on bio-inspired flight systems and bionic aerodynamics
- SARISTU:Adaptive Trailing Edge Device(ATED)design process review
- Continuous morphing trailing-edge wing concept based on multi-stable nanomaterial
