油腔结构对液体静压推力轴承承载力的影响
田助新,李波
(1.三峡大学 机械与动力学院,湖北 宜昌 443002;2.华中科技大学 机械科学与工程学院,武汉 430074;3.襄阳华中科技大学先进制造研究院,湖北 襄阳 441053)
液体静压推力轴承以其旋转精度高,油膜刚度大,减振性好等优点在重载支承领域占有重要地位[1],被广泛应用于机床、泵、定位台、望远镜、测量设备、测功器和雷达天线等领域[2-3]。
文献[1]提出了一种计算非牛顿流体润滑的圆形油腔液体静压推力轴承静态特性的新方法,通过对油膜沿半径方向的速度做均化处理,使分析过程大为简化。文献[2]针对圆形油腔液体静压推力轴承计算结果与试验结果存在较大差异的问题,在考虑供油孔区域惯性效应的前提下重新计算,缩小了理论计算与试验之间的差异,指出不能忽视小径轴承供油孔区域的惯性效应。文献[4]通过分形理论对液体静压推力轴承表面形貌进行了仿真模拟,并通过试验对仿真结果进行验证,结果表明表面粗糙度和平面度综合特征的模拟符合真实情况。文献[5]研究了多油腔液体静压推力轴承的刚度特性,结果表明不能忽视润滑油黏度对刚度的影响。文献[6]讨论了油腔结构对油膜温升的影响,结果表明矩形油腔的温升最小。文献[7]分析了油腔尺寸对机床静压轴承温度场的影响,结果表明油腔深度对温度场的影响最大。
上述研究均未涉及油腔结构对液体静压推力轴承承载能力的影响,因此,本文对不同油腔结构下液体静压推力轴承承载能力的差异进行探讨。
1 油腔结构
液体静压推力轴承承受轴向载荷,通过高压油膜将轴承与转轴隔开,起到减小摩擦的作用。3种液体静压推力轴承(简称推力轴承)的结构如图1所示。图1a中的圆形油腔推力轴承以轴承中心为圆心开有圆形油腔,ra0为供油孔半径,ra1为油腔半径,R为轴承外半径,h为封油边油膜厚度,βh为油腔区域油膜厚度,Ps为供油压力;图1b中的环形油腔推力轴承以轴承中心为圆心开有环形油腔,rb0为轴承内径,rb1为环形油腔内径,rb2为环形油腔外径,rb3为供油孔位置;图1c为扇形油腔推力轴承,本文为常见的四油腔结构,以轴承中心为圆心开有4个扇形油腔,其均匀分布在一个同心圆上,rc0为轴承内径,rc1为环形油腔内径,rc2为环形油腔外径。
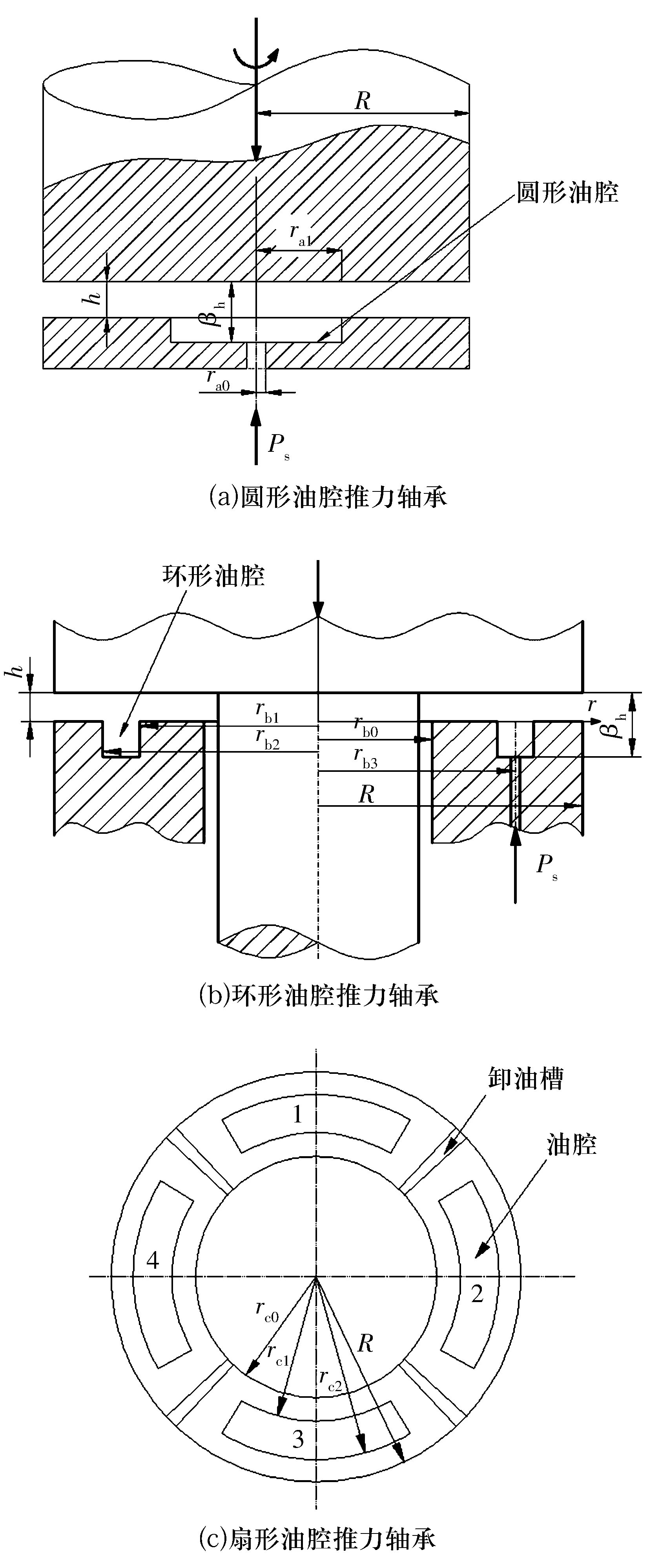
图1 3种油腔结构的液体静压推力轴承示意图
2 分析过程
忽略油膜体积力,只考虑油膜沿半径方向的惯性力,在柱坐标系下推力轴承的稳态雷诺方程为
(1)
式中:P为油膜压力;r为油膜半径;θ为周向坐标;ρ,η分别为润滑油密度和黏度;ω为轴承转速。
为简化计算过程,引入量纲一的量,即
(2)
式中:S为轴承惯性参数;W为油膜承载力。将(2)式代入(1)式,可得
(3)
圆形和环形油腔推力轴承的油膜沿竖直方向呈轴对称分布,油膜压力沿圆周方向不会发生变化,即(3)式等号左边第2项为零,因此,其雷诺方程为
(4)
(4)式为一元微分方程,可直接求解,即
P*=Sr*2+C1lnr*+C2,
(5)
式中:C1,C2为积分常数,由轴承的压力边界条件确定。
2.1 圆形油腔推力轴承
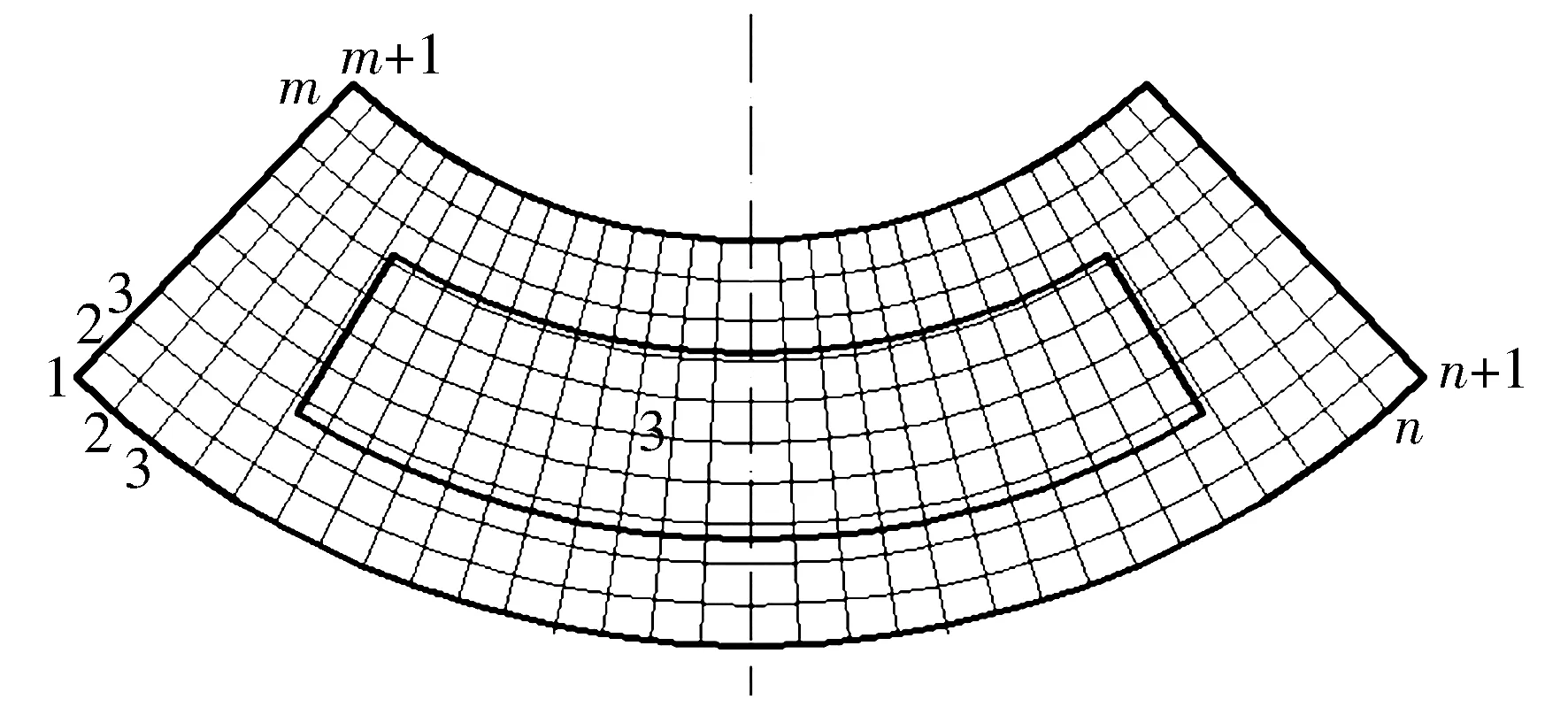
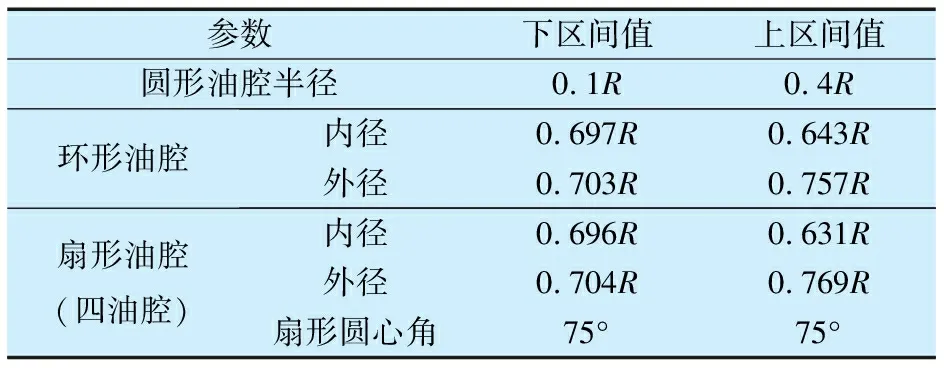
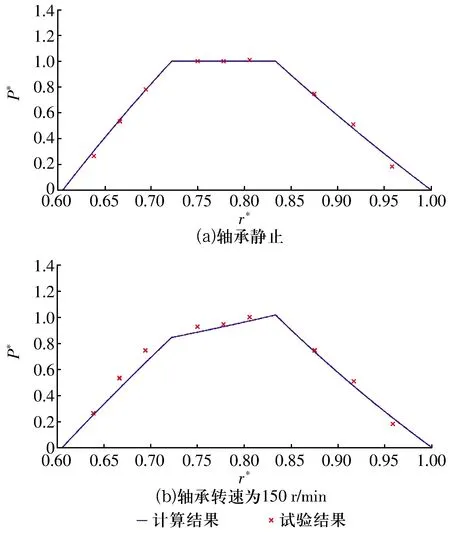
可将油膜区域分为供油孔区域(0≤r≤ra0)、油腔区域(ra0 P*= (6) 式中:Ci(i=1,2,3,4)为积分常数。引入油膜压力的2个边界条件,即 (7) (6)式共有4个未知数,因此在上述2个边界条件的基础上,再补充油膜压力和流量在r=ra1处的连续条件,可求得压力分布为 (8) 式中:β为油腔处油膜厚度与封油边处油膜厚度的比值。 将压力在量纲一的油膜半径0~1上积分可得到油膜承载力为 (9) 环形油腔与轴承的圆心相同,润滑油通过进油孔进入油腔后分别向内、外方向卸油。与圆形油腔推力轴承类似,考虑润滑油的惯性效应时油膜压力由供油系统油压P1和转动产生的惯性压力P2组成。 求解供油系统的油压P1时,不考虑轴承转动带来的影响,因此S=0,并且油腔压力恒定,此时P1为 (10) 边界条件为 (11) 由此可解得 (12) 求解转动产生的惯性压力P2时,可将油膜区域分为内封油面区域(rb0≤r≤rb1)、油腔区域(rb1 (13) 此时,只有2个压力边界条件,即 (14) 再补充油腔边界r=rb1和r=rb2处的压力和流量连续条件,即可求解(13)式中的6个未知数,即 (15) 2.2.3 推力轴承的油膜总压力和承载力 油膜总压力为 (16) 油膜总压力对面积积分得到承载力为 (17) (3)式为扇形油腔推力轴承量纲一的油膜压力限制方程其为二阶偏微分方程,无法求得解析解,需通过数值法求解。 由于4个油腔沿圆周均匀分布,以油腔3为对象对油膜划分网格,如图2所示,将其在径向m等分,每段长度为Δr,沿圆弧方向n等分,每段长度为Δθ,m和n的值根据实际情况确定。设Pi, j(i=1,2,…,m+1;j=1,2,…,n+1)为任意点的压力值,运用中间差分公式可得 图2 油腔3的油膜网格划分示意图 (18) (19) 将(18)式和(19)式代入(3)式整理可得 (20) 将各微分区域上的压力与面积相乘后累加,得到油膜承载力,即 (21) 式中:k为油腔个数,k=4。 为说明油腔结构对推力轴承承载力的影响,将3种推力轴承的油腔面积设为相等,3种结构推力轴承的几何参数见表1。 表1 3种结构推力轴承的几何参数 由图3可知,当3种推力轴承的油腔面积相等时,环形油腔轴承承载力最大,圆形油腔轴承承载力最小,原因为:对于圆形油腔轴承,油膜的惯性效应会加快润滑油卸油,进而减小承载力;对于环形油腔,油膜的惯性效应会阻碍内封油面区域的卸油,承载力增大;随着油腔面积的增大,封油面占比缩小,承载力受油腔区域承载能力的影响逐渐变大,3种轴承承载力之间的差距逐渐缩小。 图3 推力轴承承载力与油腔面积关系 为验证上述分析的正确性,在环形油腔液体静压推力轴承试验台上测量承载力(试验条件有限,只搭建了环形油腔推力轴承试验台对性能最优的环形油腔推力轴承进行验证),试验台如图4所示,环形油腔推力轴承如图5所示,其结构参数见表2。 1—下支座;2—电动机安装架;3—主轴;4—上支架;5—支承架;6—加载手柄;7—蜗轮蜗杆加载机构;8—推力调心滚子轴承;9—回转台;10—环形油腔推力轴承;11—主轴电动机;12—螺纹支承脚 图5 环形油腔推力轴承 表2 环形油腔推力轴承几何参数 为测量轴承工作时的压力分布,在推力轴承上布置了12个压力传感器,传感器量程为10 MPa,精度为0.01 MPa,分辨率为0.001 MPa,其具体分布情况如图6所示,在内封油面、油腔和外封油面每间隔90°各设置4个:内封油面上的4个压力点为3,6,9,12,其中点3布置在半径为125 mm的圆上(量纲一的径向坐标值为0.69),点6,12都布置在半径为120 mm的圆上(量纲一的径向坐标值为0.67),点9布置在半径为115 mm的圆上(量纲一的径向坐标值为0.64);油腔区域的4个点为2,5,8,11,其中点2,8都布置在半径为140 mm的圆上(量纲一的径向坐标值为0.78),点5布置在半径为145 mm的圆上(量纲一的径向坐标值为0.81),点11布置在半径为135 mm的圆上(量纲一的径向坐标值为0.75);外封油面上的4个点为1,4,7,10,其中点1布置在半径为172.5 mm的圆上(量纲一的径向坐标值为0.96),点7布置在半径为157.5 mm的圆上(量纲一的径向坐标值为0.88),点4,10布置在半径为165 mm的圆上(量纲一的径向坐标值为0.92)。 图6 压力传感器分布示意图 受试验台条件的限制,当转速超过150 r/min,压力传感器的读数跳动太大,测量结果可靠性不足,因此,将轴承转速设为150 r/min。 具体试验过程为:1)轴承静止时,通过供油孔给油腔供油,供油压力设置为1.2 MPa,待压力传感器读数稳定后转动加载手柄,通过蜗轮蜗杆加载机构沿竖直方向对轴承施加4 900 N(500 kg)的载荷,读取12个位置压力传感器的压力值;2)撤除载荷,保持供油压力不变,启动主轴电动机,将主轴转速调整到150 r/min,沿竖直方向对轴承施加1 470 N(150 kg)的载荷,读取12个位置的压力值。 试验值与理论计算值如图7所示,当轴承静止时,试验值与理论计算值的一致性良好;当轴承以150 r/min转动时,试验值与理论值较为符合,误差保持在8%以内,说明了本文理论分析的正确性。 图7 环形油腔推力轴承油膜压力计算值与试验值对比 讨论了推力轴承油腔结构(圆形、环形和扇形)对其承载力的影响,通过理论分析得到3种油腔结构的推力轴承承载力,通过对比发现:在油腔面积相同时,环形油腔推力轴承承载力优于圆形和扇形油腔轴承。在环形油腔液体静压推力轴承试验台上测得轴承油膜压力分布与本文理论计算结果基本一致,说明本文理论分析的正确性。在需较大承载能力的情况下,液体静压推力轴承的油腔结构可优先选择环形油腔。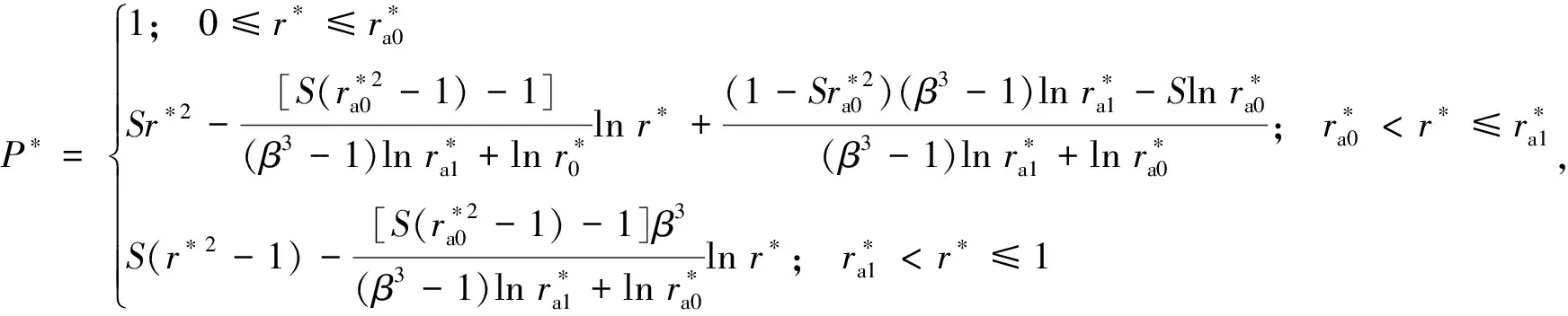
2.2 环形油腔推力轴承

2.3 扇形油腔推力轴承
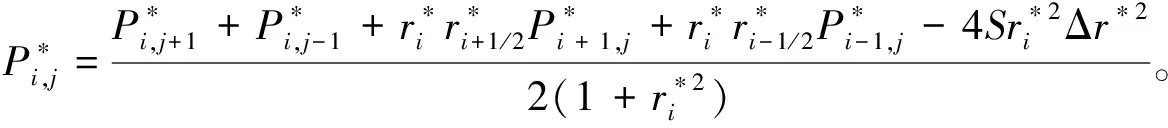
2.4 结果对比

3 试验验证




4 结束语

