定位预紧和定压预紧下角接触球轴承动态特性研究
李小虎,张燕飞,万少可,李森
(1.西安交通大学 机械工程学院,西安 710049;2.现代设计及转子轴承系统教育部重点实验室,西安 710049;3.西安理工大学 机械与精密仪器工程学院,西安 710048)
0 引言
预紧作为调控角接触球轴承服役性能的重要参数,对轴承性能的提升具有重要作用。合理的预紧可以增加轴承刚度,降低振动噪声,提高旋转精度,抑制轴承打滑,延长轴承使用寿命,在高精密轴承系统中的作用尤其明显[1]。数控机床精密主轴轴承系统通常在高速轻载、低速重载等多变复杂工况下工作,选择合理的预紧方式及预紧力是确保角接触球轴承的刚度、温度、旋转精度等服役性能满足要求的关键因素。因此,开展不同预紧方式下角接触球轴承的动态特性分析可为机床主轴轴承系统的性能分析提供理论依据。
传统的轴承预紧技术可分为定位预紧和定压预紧2种方式,国内外学者针对不同预紧方式对滚动轴承性能变化的影响开展了大量理论及试验研究,并取得了丰硕成果:文献[2]建立了轴承拟静力学模型并通过解析法求解轴承刚度矩阵,然而其求解过程中忽略了滚动体所受陀螺力矩的影响;文献[3]在分析高速精密角接触球轴承接触载荷和钢球滚动规律的基础上,研究了轴承预紧载荷与转速之间的映射规律,提出了防止钢球陀螺滑动所需的最小预紧载荷;文献[4]对角接触球轴承预紧的类型及工作原理进行了分析,给出了预紧方式的选择原则和确定预紧力的计算方法,但并未涉及轴承刚度的求解计算;文献[5]分析了预紧力对高速角接触球轴承中钢球与内、外圈的接触刚度以及轴承整体径向刚度、轴向刚度和角刚度的影响规律,但该研究中未明确轴承的具体预紧方式;文献[6]考虑了轴承预紧力以及转动过程中导致滚动体与滚道之间的接触变化,基于有限元方法建立轴承接触模型并计算了轴承的刚度矩阵,该方法也未涉及轴承的预紧方式;文献[7]建立了轴承拟静力学模型并使用全解析法求解轴承的刚度矩阵,但只分析了轴承定压预紧的情况;文献[8]分析了轴承定位预紧和定压预紧对主轴-轴承动态刚度的影响,得出高速工况时在切削载荷作用下定位预紧比定压预紧更能有效维持主轴动态刚度的结论;文献[9]建立了轴承五自由度拟静力学模型并提出了轴承时变刚度,研究了在静态、动态外载荷作用下轴承刚度的波动情况,但只分析了定压预紧工况下的轴承力学性能变化;文献[10]提出了在定压预紧和定位预紧方式下计算轴承刚度的方法,并且分析了转速、预载荷以及沟道曲率对轴承刚度的影响,然而其求解刚度时采用了近似计算方法,虽然求解速度快,但在高速工况下计算精度差且只能计算主刚度。
综上所述,目前的轴承拟静力学求解模型大都基于定压预紧方式,对于定位预紧方式下轴承动态特性的研究仍需进一步完善,因此有必要对2种预紧方式下的轴承求解模型进行综合对比分析,研究不同预紧方式下角接触球轴承的接触角、接触力、离心力、刚度等动态特性的变化规律,为数控机床精密主轴轴承系统的设计与分析提供理论支撑。
1 角接触球轴承五自由度拟静力学模型的建立
1.1 轴承几何关系的分析
在轴向载荷Fx,径向载荷Fy和Fz以及弯矩My和Mz的作用下,角接触球轴承内、外圈之间产生轴向相对位移δx,径向相对位移δy和δz,以及相对角位移θy和θz,建立的直角坐标系如图1所示。

图1 角接触球轴承受力及球分布图
假定轴承内部有Z个球且在轴承内均匀分布,则第j个球的位置角为
ψj=ψ1+2π(j-1)/Z。
(1)
静止状态下,轴承内沟道曲率中心、外沟道曲率中心与球心3点共线。高速运转时,球受到离心力和陀螺力矩的作用,球心位置相对静止状态下发生变化,轴承内部几何关系如图2所示。
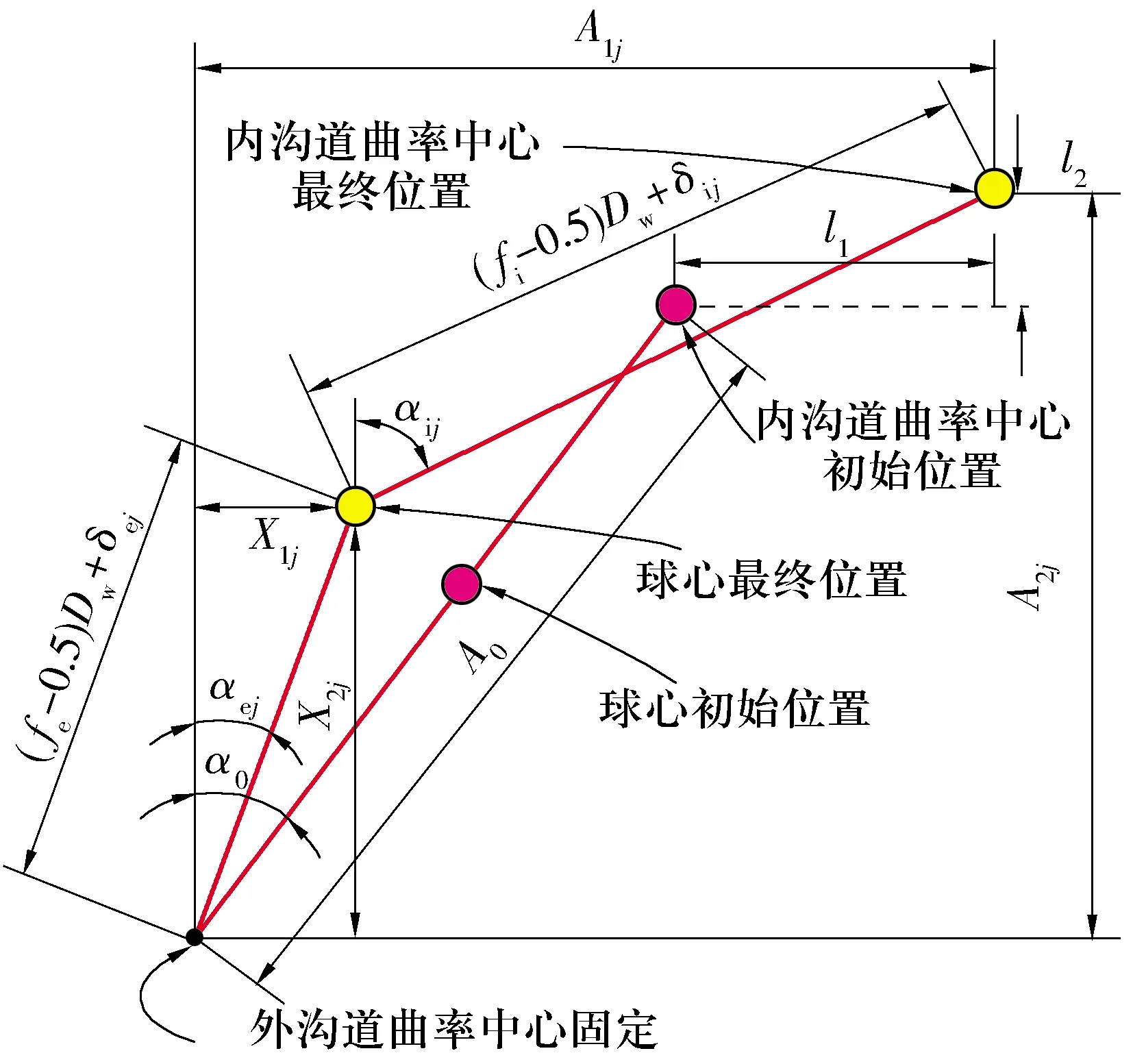
图2 轴承内外圈与球的几何关系
未受力前,轴承内、外沟道曲率中心距为
A0=(fi+fe-1)Dw,
(2)
式中:fi,fe分别为内、外沟道曲率半径系数;Dw为球径,mm。
第j个球处,内、外沟道曲率中心之间的轴向距离A1j和径向距离A2j为
(3)
(4)
(5)
式中:Ri为内沟道曲率中心轨迹半径,mm;Dpw为球组节圆直径,mm。
同样,球与内、外圈之间接触角αij,αej的三角函数表达式为
(6)
式中:X1j,X2j分别为第j个球的球心与外沟道曲率中心之间的轴向距离和径向距离;δij,δej分别为第j个球与内、外圈的接触变形量。
根据勾股定理可得
(7)
1.2 角接触球轴承受力分析
角接触球轴承受力分析包括球的局部受力分析和套圈的整体受力分析。
1.2.1 球的受力分析
球的受力分析如图3所示,轴承在高速转动时,球除承受与内、外圈的接触载荷外,还受到离心力和陀螺力矩的作用。球在竖直和水平方向上平衡方程为

图3 球受力平衡图
(8)
式中:Qij,Qej为第j个球与内、外圈的接触载荷,N;Mgj为第j个球的陀螺力矩,N·mm;Fcj为第j个球的离心力,N;λij,λej分别为内、外沟道的载荷分配系数,对于外沟道控制理论,λij=0,λej=2,否则λij=1,λej=1。
根据赫兹接触理论,球与内、外圈的法向接触载荷与变形的关系为
(9)
第j个球承受的离心力和陀螺力矩为
(10)
(11)
式中:m为球质量,kg;J为球转动惯量,kg·mm2;ω为内圈角速度,rad·s-1;ωm为球公转角速度,rad·s-1;ωR为球自转角速度,rad·s-1;β为球姿态角,(°)。
第j个球的自转角速度与公转角速度之比为
(12)
(13)
(14)
γ=Dw/Dpw。
ωm/ω和tanβ的取值与沟道控制理论有关,选择标准见表1和表2,其中L为与接触面积有关的第二类完全椭圆积分。

表1 内、外沟道控制理论选择标准
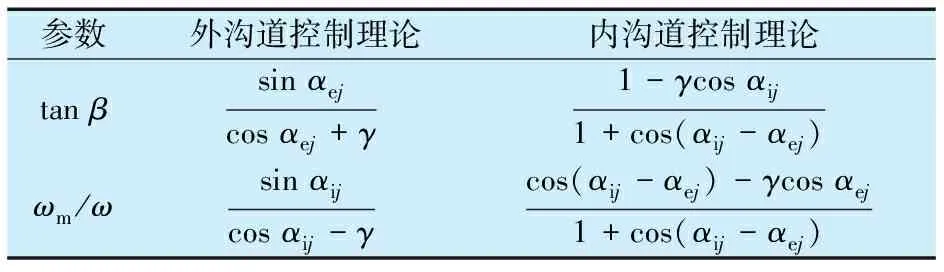
表2 姿态角和轨道速度与内圈转速之比的计算
1.2.2 整体受力分析
将球与内圈之间的接触载荷进行叠加,得到轴承内圈的受力平衡方程为
。(15)
2 不同预紧方式下轴承力学模型的求解
2.1 定压预紧和定位预紧
不同预紧方式下,轴承动态特性的差异较大:对于定压预紧(图4a),用刚度较小的弹簧对外圈施加预紧力Fx,其在轴承运转过程中保持不变,内、外圈相对位置可以发生变化;对于定位预紧(图4b),组装之后用锁紧螺母拧紧消除间隙δx即可使2套轴承均处于预紧状态,不考虑热变形的影响时轴承初始压入量δx保持不变,即轴承运行过程中内、外圈的相对位置保持不变。

图4 滚动轴承轴向预紧方式示意图
2.2 定压预紧和定位预紧轴承刚度矩阵求解
根据刚度的定义,求出载荷对位移的偏导数,即轴承刚度矩阵的解析表达式,然后代入具体数值求得轴承在不同工况下的刚度矩阵,该方法求解的是切线刚度,求解结果精度高。在求解过程中,通常将每个球的方程称为局部方程(即(7)式和(8)式),轴承整体受力方程称为全局方程(即(15)式)。每个球的求解变量X={X1,X2,δi,δe}j称为局部求解变量,j=1,2,…,Z。将f={Fx,Fy,Fz,My,Mz}称为全局载荷变量,d={δx,δy,δz,θy,θz}称为全局位移变量。由(15)式可知,整体轴承的受力与轴承内每个球的受力有关,因此需要先求解每个球的平衡方程,联立(7)式和(8)式进行求解。解析法求解轴承刚度矩阵是将轴承承受的外载荷f对轴承内外圈相对位移d求偏导数形成的5×5阶矩阵。
2.2.1 定压预紧模型求解
在定压预紧时,轴承边界条件为f={Fx,Fy,Fz,My,Mz},所需求解变量包括5个全局变量d={δx,δy,δz,θy,θz}以及4Z个局部变量X={X1,X2,δi,δe}j。首先,根据静力学模型求解结果给定一个初始迭代值d0={δx,δy,δz,θy,θz}0;然后,求解(7)式和(8)式得到局部变量X={X1,X2,δi,δe};最后,根据(15)式计算此次的载荷向量以及轴承刚度矩阵。当不满足收敛条件时,用轴承刚度矩阵对全局位移d进行修正后继续求解(7)式和(8)式,直到满足收敛条件为止。
2.2.2 定位预紧模型求解
在定位预紧时,已知的量是轴承压入量,而不是轴向外载荷,因此轴承边界条件为f={δx,Fy,Fz,My,Mz},称为混合边界条件,所需求解的变量包括5个全局变量d={Fx,δy,δz,θy,θz}以及4Z个局部变量X={X1,X2,δi,δe}j。由于轴向载荷求解变量Fx只存在于全局方程的轴向平衡方程中,则局部方程以及全局方程的后4个方程共含有4Z+4个求解变量,而不包含轴向载荷求解变量,因此只需先求解4Z个局部变量X={X1,X2,δi,δe}和d={δy,δz,θy,θz}。此时的解法同定压预紧的情况,由于轴承压入量已知,因此在反复迭代过程中无需对轴向位移进行修正,将初始迭代向量设置为d0={δy,δz,θy,θz}0,不满足收敛条件时用轴承刚度矩阵对轴承全局位移d进行修正即可,此时刚度矩阵为4×4阶。
不同预紧方式下角接触球轴承模型的求解流程如图5所示,图中:d0为全局变量的迭代初值,可采用静力学求解结果;f为给定的外载荷,fn为迭代过程中所有球对内圈的接触力之和;ε1,ε2为误差向量,εtol1和εtol2为容许误差。每次迭代后若不满足容许误差,则用轴承的刚度矩阵修正迭代初值d0后继续对(7)式和(8)式进行求解,直到满足最终求解误差小于给定的容许误差为止。
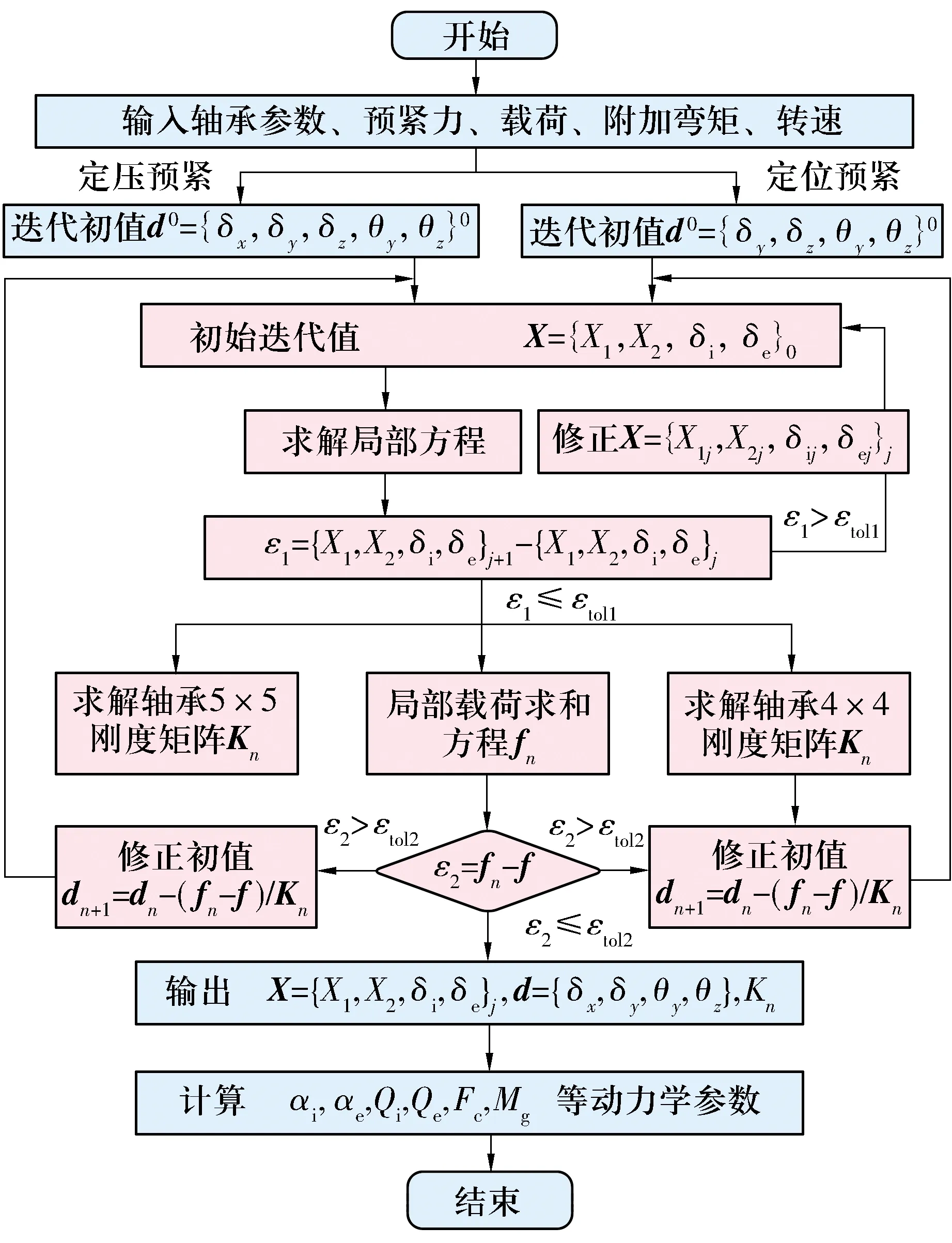
图5 不同预紧方式下轴承模型求解流程
3 轴承的动态特性分析
轴承的动态特性包括球与内、外圈的接触力和接触角,球的离心力、陀螺力矩以及轴承刚度。轴承的动态特性受预紧方式、预紧力、转速、径向载荷、球材料等因素的影响。本文以NSK7008C角接触球轴承(基本参数见表3,套圈和球的材料均为轴承钢)为例,研究轻、中、重预紧(轻、中、重预紧根据NSK轴承手册选取,对应的预紧力和预紧量见表4)情况时,轴承动态特性在不同转速下的变化规律并进行综合对比分析。

表3 NSK7008C轴承的基本参数

表4 NSK7008C轴承的预紧方式及预紧力
3.1 定压预紧下的轴向变形和定位预紧下的轴向载荷随转速的变化
如图6所示,定压预紧下轴承的轴向变形量随转速的增大而减小,这是由于定压预紧状态下轴承内、外圈之间可以相互浮动,随着转速的升高,球的离心力逐渐增大,对外圈的作用力也随之增加,将迫使内、外圈远离;此外,轴承初始预紧力越大,在高速(转速大于6 000 r/min,下同)下抵抗球对外圈作用力的能力越强,轴承的轴向变形量随转速的变化越小。

图6 定压预紧下轴向变形量随转速的变化
如图7所示,定位预紧下轴承的轴向载荷随转速的升高而增大,这是由于定位预紧状态下轴承内、外圈之间的相对位置固定,高速下球的离心力作用导致球对外圈的作用力增大且无法释放,最终使轴向载荷增大。
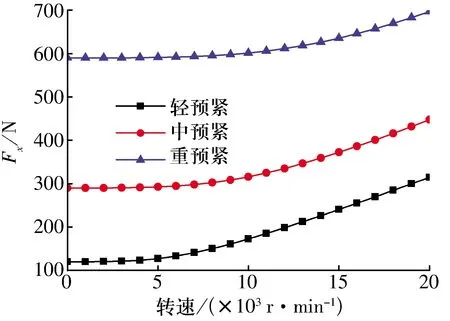
图7 定位预紧下轴向载荷随转速的变化
3.2 定压预紧与定位预紧下球接触载荷随转速的变化
不考虑球所承受的陀螺力矩,其径向和轴向平衡方程为
(16)
由(16)式可得
(17)
由(17)式可得αe<αi,即在离心力的作用下,球与内圈的接触角增大,与外圈的接触角减小;由(16)式可得Qe>Qi,即在离心力的作用下,球与内圈的接触载荷小于球与外圈的接触载荷。
在轴向预紧力作用下,不考虑接触角随转速变化时,每个球与内、外圈的法向接触载荷为
(18)
定压预紧或定位预紧时,不同预紧力下球与内、外圈的接触载荷随转速的变化如图8所示,由图可知:

图8 不同预紧力下接触载荷随转速的变化
1)球与内、外圈的接触载荷均随着初始预紧力的增大而增大。
2)在定压预紧状态下,由于转速升高使内接触角增大,球与内圈的接触载荷随转速升高而减小,但这种减小趋势并不明显。
3)在定位预紧状态下,球与内圈的接触载荷随转速升高先减小后增大。在转速较低时,轴向载荷增加并不显著,与此同时接触角增大,因此接触载荷变小;随着转速升高,轴向载荷迅速增大并占主导因素,球与内圈的接触载荷随之增大。
4)高速运行工况下,对于定压预紧,由于惯性力的作用,球有脱离内沟道而压向外沟道的趋势,导致球与外圈的接触角减小且接触载荷增加;对于定位预紧,不仅离心力使球与外圈的接触角减小,而且轴向载荷也随着转速升高而增大;因此,在高速运行工况下,定位预紧时球与外圈的接触载荷比定压预紧时大。
3.3 定压预紧与定位预紧下球与沟道的接触角随转速的变化
定位预紧或定压预紧时,不同预紧力下球与内、外圈的接触角随转速的变化如图9所示,由图可知:

图9 不同预紧力下接触角随转速的变化
1)静态下球与内、外圈的接触角相同,且接触角随着初始预紧力增大而增大。
2)高速运行工况下,由于离心力和陀螺力矩的作用,球与内圈的接触角增大,球与外圈的接触角减小;定位预紧与定压预紧时,球与内圈的接触角相差不大,但定位预紧时球与外圈的接触角更大,说明定压预紧时球受到的离心效应更明显。
3)转速为20 000 r/min,轻、中、重预紧工况下,定压预紧时球与外圈的接触角相对定位预紧时分别减小45.6%,18.2%,5.2%,这是由于高速下球有压向外沟道的趋势,然而定位预紧的轴向载荷随转速增大而增大,抑制了接触角随转速的减小。计算结果也表明,预紧力越大,定压预紧与定位预紧时球与外圈的接触角相差越小。
3.4 不同预紧方式下轴承刚度随转速的变化
定位预紧或定压预紧时,不同预紧力下轴承刚度随转速的变化如图10所示,由图可知:
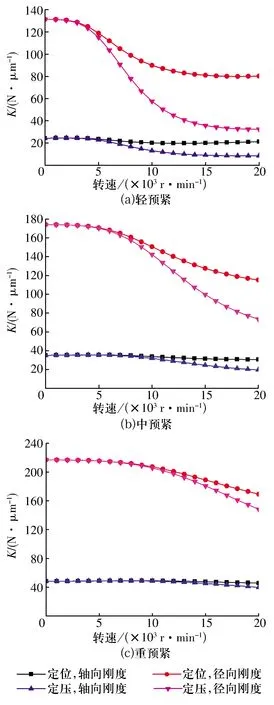
图10 不同预紧力下轴承刚度随转速的变化
1)静态下,轴承的轴向刚度和径向刚度随预紧力增大而增大。
2)在高速运行工况下,轴承的轴向刚度和径向刚度均随着转速升高而衰减,但衰减的程度略有不同,定位预紧时轴承的刚度明显大于定压预紧时。在转速为20 000 r/min,轻、中、重预紧工况下,定压预紧轴承比定位预紧轴承的轴向刚度分别减小了60.1%,36.2%,13.1%,径向刚度分别减小了59.5%,36.1%,12.4%,原因是定位预紧轴承的轴向载荷随转速的升高而增大,抑制了刚度随转速的减小。
4 结论
构建了角接触球轴承拟静力学模型,研究了不同预紧方式角接触球轴承的动态特性分析计算方法,探索不同预紧方式、转速、预紧力等因素对轴承动态特性的影响规律,得出以下结论:
1)定压预紧轴承的轴向变形量随转速升高而减小,定位预紧轴承的轴向载荷随转速升高而增大。
2)高速运行工况下,定位预紧时球与外圈的接触载荷比定压预紧时的大。
3)静态工况下,球与内、外圈的接触角相等且接触角随初始预紧力增大而增大;高速运行工况下,预紧力越大,定压预紧时球与外圈的接触角与定位预紧时的差值越小。
4)轴承刚度随预紧力增大而增大,随转速升高而减小。高速、初始预紧力相等工况下,定位预紧轴承的轴向刚度和径向刚度均大于定压预紧轴承。

