基于最小熵反褶积的动车组牵引电动机轴承故障诊断方法

李伟

(中车永济电机有限公司 西安中车电气研究院，西安 710000)

牵引电动机作为高速动车组重要的组成部分，其安全运行对于高速动车组的发展具有重要的现实意义[1-4]。轴承是牵引电动机的核心部件，在各种复杂工况下运行时容易产生滚动体变形、磨损、腐蚀、裂缝等各种缺陷[5-8]，严重影响牵引电动机的运行状态。当牵引电动机轴承出现各种故障[9-12]时，传感器采集到的振动信号往往含有大量的背景噪声，有效信号常被噪声淹没[13-16]，故障特征难以提取，因此快速准确地提取轴承故障特征非常重要。

最小熵反褶积(Minimum Entropy Deconvolution,MED)算法[17-19]是一种应用较为广泛的自适应信号处理方法，文献[20]将MED作为集合经验模态分解的前置滤波器进行齿轮箱的故障诊断，通过仿真与试验证明该方法对微弱故障具有较好的实用性。

针对牵引电动机运行工况复杂，轴承故障引起的冲击相对较小，冲击信号通常淹没在环境噪声中，传统的时频域分析、包络谱分析等算法不能完全适用的问题，本文采用最小熵反褶积算法对复杂信号进行处理，将包络谱熵作为适应度函数，用粒子群优化算法对滤波步长L进行优化使最小熵反褶积算法达到最优，并通过试验验证该算法对牵引电动机轴承故障特征提取的有效性。

1 理论分析

1.1 最小熵反褶积

最小熵反褶积算法通过寻找一个最优逆滤波器在解反卷积过程中突出信号脉冲，并以峭度值最大为迭代停止条件，尽可能减小原始信号的混乱程度，达到消除背景噪声与其他环境干扰的目的。实际采集到的滚动轴承振动信号可表示为

y(n)=h(n)*x(n)；n=1,2，…，N,

(1)

式中：x(n)为故障冲击信号；h(n)为传递函数。

解卷积的目的是寻找一个最优逆传递函数w(n)，由输出y(n)恢复冲击信号x(n)，即

x(n)=w(n)*y(n)。

(2)

输入信号x(n)经过与传递函数的卷积后，本身会变得复杂，最小熵反褶积算法相当于解卷积的过程，将输出信号y(n)还原到输入信号x(n)。

利用w(n)是否达到最优衡量x(n)的熵值，对(2)式进行解卷积所得新输入信号的表达式为

(3)

式中：w(n)为逆滤波器；L为滤波器长度。

最小熵反褶积的迭代算法如图1所示，其中

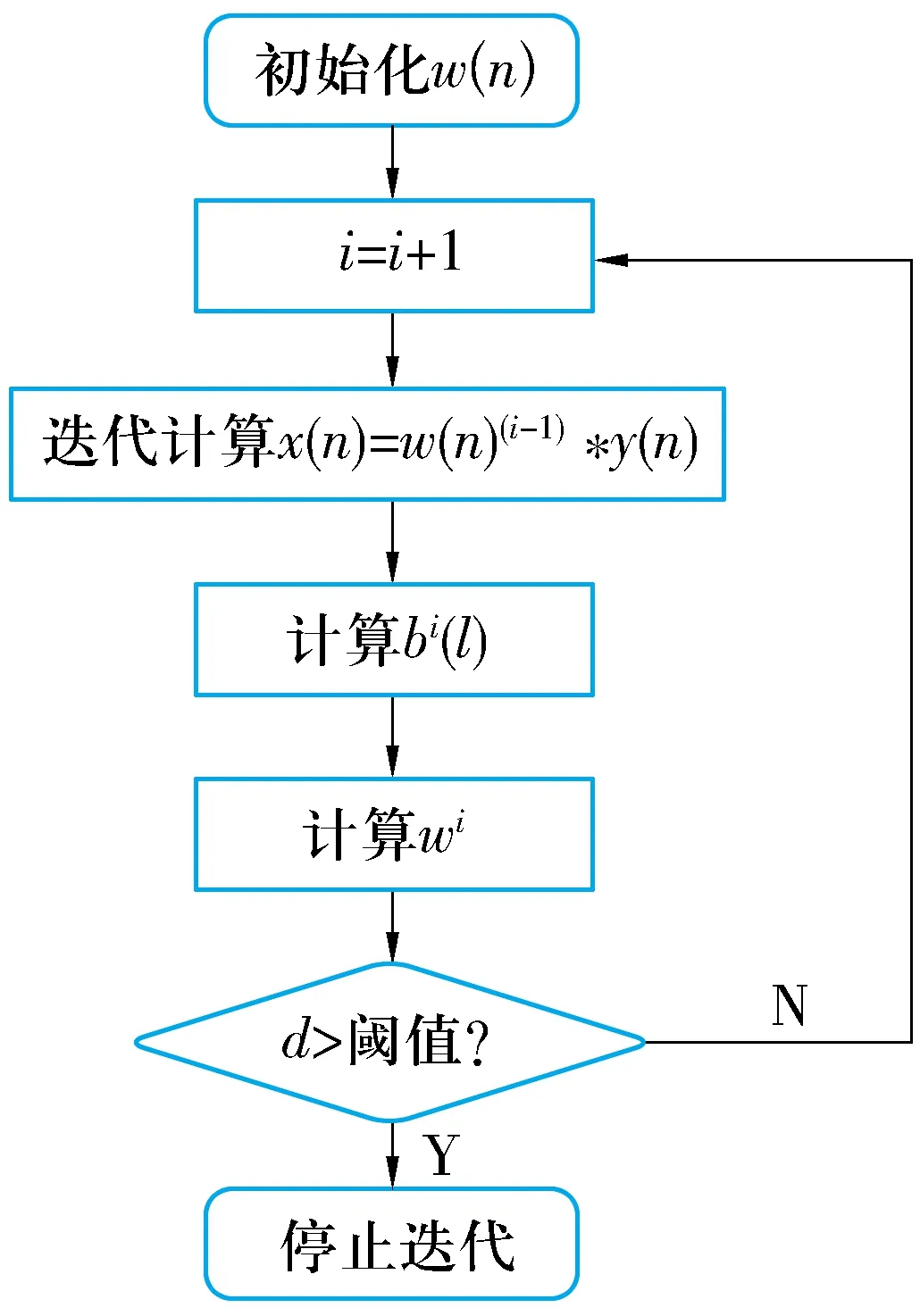
图1 MED算法迭代流程

(4)

(5)

wi=A-1bi(l)，

(6)

(7)

式中：A为y(n)的托普利兹自相关矩阵。

1.2 量子行为粒子群优化算法

研究人员受到粒子群算法和量子力学的启发，经过不懈的探索，提出了兼具粒子群算法和量子力学优点的量子行为粒子群优化(Quantum Particle Swarm Optimization，QPSO)算法[21]。

在N维空间中，由于吸引子的原因，量子行为粒子群优化算法将粒子的运行轨迹逐渐收敛，从而达到算法收敛的目的。若群体中粒子规模为M，每个粒子为N维，则第i个粒子的吸引子为pi=(pi,1,pi,2,…,pi,N)，其数学坐标可表示为

(8)

(9)

式中：c1，c2为非负数学习因子；r1，r2为分布于[0,1]的随机数；pi,j(t)为第t代粒子i的个体最优位置；Gj(t)为第t代粒子的全局最优位置。

粒子在势阱作用下以p点为中心进行运动，粒子i第j维的进化可表示为

(10)

式中：S为粒子群势阱的特征长度；m为粒子的质量；h为普朗克常数；u为区间(0,1)上的均匀分布随机数；γ为参数，其由 1.0 线性递减至0.5时具有较好的效果。

1.3 基于量子行为粒子群优化算法优化滤波步长

选用包络谱熵作为量子行为粒子群优化算法优化滤波步长L的适应度函数[22]。为使降噪后信号突出更多有效的连续性周期，包络谱熵越小越好。

信号x(t)的希尔伯特变换为

(11)

x(t)与h(t)构成的新信号为

Z(t)=x(t)+jh(t)，

(12)

则包络信号可表示为

(13)

将包络谱与信息熵结合得到的包络谱熵为

(14)

式中：HX(i)为包络谱；He为包络谱熵。

将包络谱熵归一化处理可得

(15)

量子行为粒子群优化算法对滤波步长L的优化过程如下：

1)确定量子行为粒子群优化算法各参数的值；

2)设置t=0，初始化各参数；

3)将包络谱熵作为适应度函数，计算量子行为粒子群中微粒的适应度值，通过与之前计算所得适应度值的比较不断更新粒子位置；

4)计算粒子群的全局最优位置，并与之前的全局最优位置比较，不断更新粒子的最优位置；

5)更新粒子的最新位置；

6)迭代次数达到最大时结束程序，若迭代次数没有达到最大，则t=t+1，并返回第3步重复进行，直到迭代次数达到最大。

2 故障诊断流程

根据对最小熵反褶积、量子行为粒子群优化算法和包络谱熵的理论分析，设置的牵引电动机轴承故障诊断流程如图2所示。

图2 牵引电动机轴承故障诊断流程

3 试验验证

牵引电动机轴承专用试验机如图3所示，主要由加载系统、驱动系统、润滑系统、电气控制与计算机测试系统组成。在A处(6311轴承)和B处(NU214轴承)各安装1个PCB356B21振动传感器用于监测试验轴承的振动情况，试验转速为2 858 r/min，采样频率为25 600 Hz，试验轴承的基本参数见表1。

图3 牵引电动机轴承试验机结构示意图

表1 牵引电动机轴承结构参数

为从工程应用角度验证本文所提方法对动车组牵引电动机轴承故障特征提取的可行性与有效性，利用上述台架试验得到的数据进行验证。

6311轴承内圈故障如图4所示，其振动信号和包络分析结果如图5所示。未优化时，随机选取的滤波步长L为200，通过最小熵反褶积算法处理的信号如图6所示，提取出了65 Hz等无用频率以及大量杂乱无章的干扰信号，说明随机选取滤波步长时最小熵反褶积算法不能有效处理信号，需要对滤波步长L进行最优处理。

图4 6311轴承内圈故障示意图

图5 6311轴承内圈故障振动信号的时域波形和包络谱

图6 L为200时6311轴承内圈故障振动信号的MED处理结果

由于最小熵反褶积算法中滤波步长对信号处理的影响较大，因此，采用包络谱熵作为适应度函数，使用量子行为粒子群优化算法对滤波步长进行优化，优化后的滤波步长取值为495，再次使用最小熵反褶积算法对相同的振动数据进行处理，结果如图7所示，包络谱图中成功提取出了转频75 Hz以及牵引电动机轴承内圈故障频率375 Hz，从试验数据方面验证了本文所提方法的有效性和可靠性。

图7 L为495 时6311轴承内圈故障振动信号的MED处理结果

为进一步验证该算法的有效性，使用6311轴承钢球故障(图8)数据进行验证，量子行为粒子群优化算法得到的滤波步长为135，钢球故障振动信号的MED处理结果如图9所示，其包络谱中成功提取出了18 Hz的钢球故障特征频率及其2倍频。

图8 6311轴承钢球故障示意图

图9 L为135时6311轴承钢球故障振动信号的MED处理结果

同样，对安装于B处的NU214轴承(滚子故障如图10所示)进行分析，使用量子行为粒子群优化算法得到的滤波步长为53，采用优化后的MED对NU214轴承滚子故障信号进行分析，结果如图11所示。

图10 NU214轴承滚子故障示意图

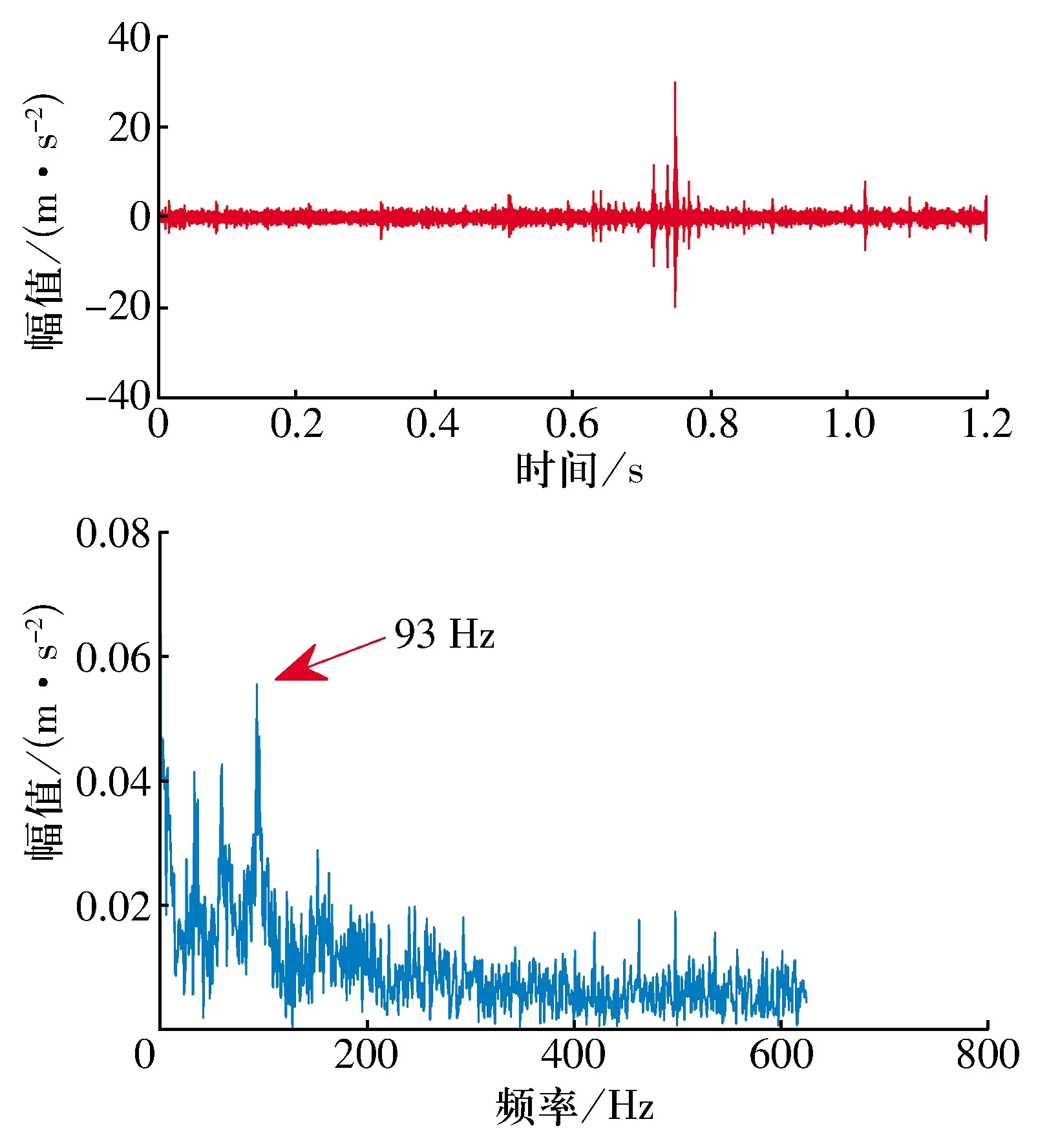
图11 L为53时NU214轴承滚子故障振动信号的MED处理结果

由图11可知：包络谱图中成功提取出了93 Hz的NU214轴承滚子故障特征频率，从不同类型的故障方面验证了本文所提方法提取牵引电动机轴承故障特征的有效性和可靠性。

4 结束语

基于量子行为粒子群优化算法以及包络谱熵在处理振动信号中的优势，使用包络谱熵为适应度函数，采用量子行为粒子群优化算法对最小熵反褶积算法的滤波步长L进行优化。通过高速铁路动车组牵引电动机轴承台架振动数据，从工程实际角度验证了本文所提方法能够改进最小熵反褶积算法的缺陷，改进后的最小熵反褶积算法能够有效提取高速铁路动车组牵引电动机轴承的故障特征。