谐波齿轮双圆盘波发生器设计与有限元仿真分析＊

吴鸿雁 王玉琦 李香飞

1天津职业技术师范大学工程实训中心 天津 300222

2天津工业大学天津市现代机电装备技术重点实验室 天津 300387

0 引言

谐波传动是20世纪50年代发展起来的一种新型传动技术。具有传动比大、传动精度高、质量轻和承载能力大等诸多优点，被广泛应用于航空航天[1]、机器人关节和柔性传动机构[2,3]等众多领域。随着社会发展，机器人被大量应用于物料搬运、工厂自动化生产线等用以代替人的繁重劳动，谐波减速器作为机器人中的核心部件越来越受到重视和关注，相关高校和企业对其的研发、制造投入也越来越大。谐波减速器主要包括3个构件：柔轮、刚轮和波发生器。在装配前柔轮的剖面是圆形，装配后在波发生器的强制作用下，迫使柔轮变为非圆形。波发生器对于柔轮的变形状态非常重要，双圆盘波发生器作为一种结构简单、包角区间大以及承载能力强的波发生器类型，受到众多学者的关注，对其作出了很多有价值的研究。

陈晓霞等[4]基于力学方法，计算了双圆盘波发生器作用下柔轮的周向伸长量，并建立有限元模型验证了理论方法的可行性。周清华[5]采用有限元方法研究了柔轮在不同波发生器作用下的应力和变形，提出了采用双圆盘波发生器来改善柔轮应力分布和提高承载能力的设计方案。付军锋等[6]通过有限元手段对比分析了不同波发生器作用下柔轮空载时的应力分布状态，研究结果表明，采用双圆盘波发生器时，柔轮壳体上应力最小。蒋素清[7]建立了椭圆和双圆盘波发生器分别与柔轮接触分析的有限元模型，得出双圆盘波发生器作用下柔轮应力较小，更适用于重载传动。Ianici S and Ianici D[8,9]分析了双圆盘波发生器对柔性轮壁特征点应力分布和位移变化的影响。由于波发生器结构特性，两个圆盘轴向位置并非处在同一个平面，从而造成柔轮变形存在差异[10]。为了减小这种影响，伊万诺夫[11]提出取圆盘计算半径的0.1倍值作为圆盘与柔轮内壁的接触宽度bc。沈允文[12]则提出取圆盘厚度1/3作为接触宽度bc。伊和沈的解决方案虽然都能在一定程度减小圆盘波发生器作用下柔轮变形差异，但是依旧未能完全消除。

本文基于直母线假定，区别于传统波发生器两圆盘完全相同，在前者的基础上对双圆盘波发生器的结构设计进一步改进，提出对波发生器两个圆盘结构参数进行独立设计计算。基于HD公司产品算例，计算改进前、后两组波发生器参数，建立参数化双圆盘波发生器与柔轮接触分析有限元模型，对比分析柔轮的变形特征和应力分布状态。

1 圆盘波发生器计算理论

1.1 双圆盘波发生器结构

如图1所示，α1为前盘作用下柔轮变形产生锥角，α2为后盘作用下柔轮变形产生锥角，bc为波发生器与柔轮接触宽度。

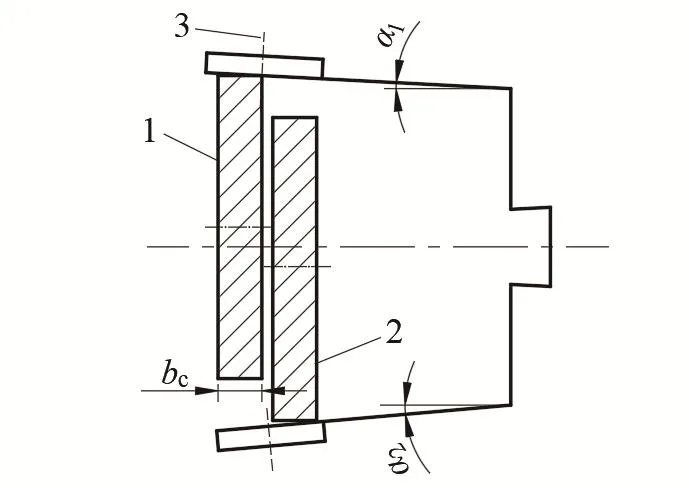
图1 双圆盘波发生器作用下柔轮变形示意图

由于波发生器结构特性，前、后圆盘轴向位置并非同一平面内，当波发生器装入柔轮时，筒体产生的锥角α1≠α2，导致上、下两部分柔轮变形特征存在差异，影响传动精度和啮合性能。因此，下文将以计算截面达到给定径向变形量为目标，对波发生器前、后圆盘参数分别进行设计计算。

1.2 波发生器前圆盘计算

如图2所示，R1为前圆盘的计算半径，e1为前盘轴线相对于波发生器轴线的偏心距，γ为柔轮对圆盘的包角，w0为柔轮最大径向变形量。装配变形前，柔轮的中面为圆形，在波发生器作用下，变为矢径为ρ的非圆形。

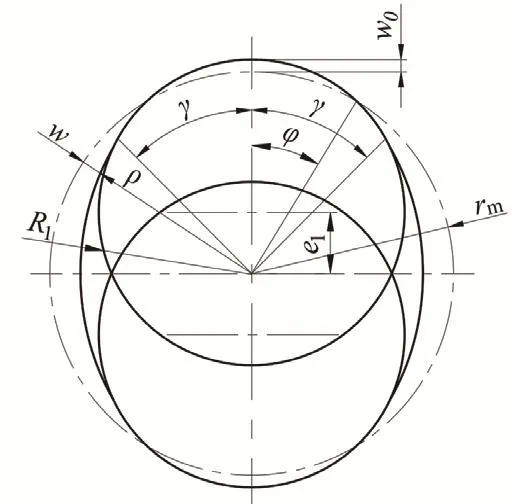
图2 柔轮中性层变形剖面

中性层任意位置φ角位置处的矢径

式中：rm为变形前柔轮中性层曲线的半径，w(φ)为中性层任意φ角位置处的径向位移。

对前圆盘结构参数计算

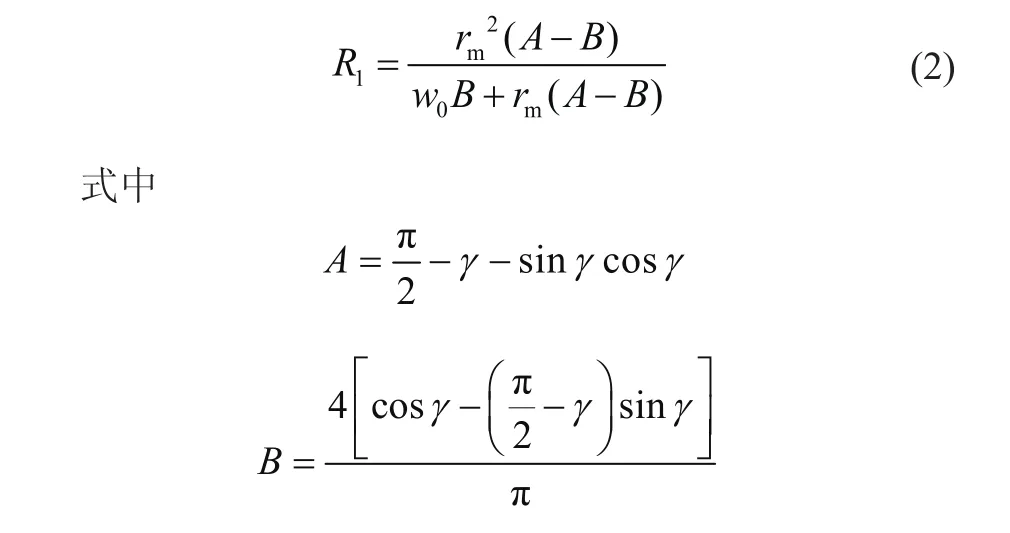
通常情况下，w0和rm是已知的。故只要给定包角γ就能够求出圆盘计算半径R。

又根据图中变形关系，可得前盘偏心距

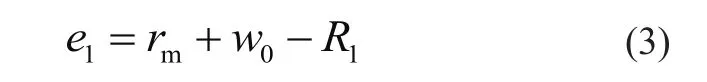
前文介绍关于波发生器圆盘与柔轮的接触宽度bc的取值，参考文献[11]和[12]各自都提出了一种方法，由于二者方法的差别非常小，因此本文只采用参考文献[11]的方法，即取

1.3 波发生器后圆盘计算

区别于传动双圆盘波发生器，根据柔轮直母线假定，对后圆盘结构参数独立计算，如图3所示。l1为中截面到柔轮杯底距离，R2为波发生器后盘计算半径，e2为后盘偏心距，δ为筒环宽度。

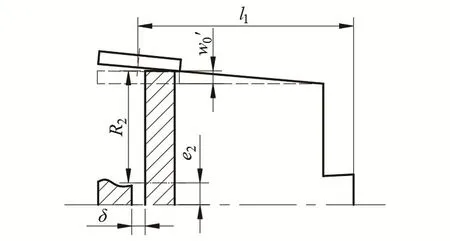
图3 后圆盘作用下柔轮变形示意图

根据图中几何关系，柔轮与后圆盘接触位置的处径向变形量

后圆盘计算半径

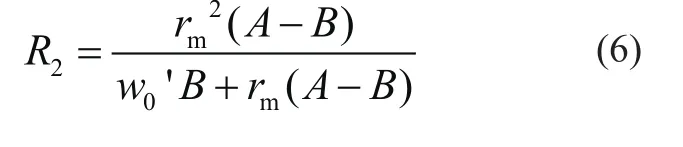
后圆盘轴线偏心距

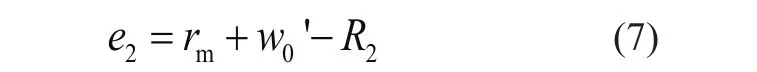
根据上述改进后圆盘波发生器设计理论，前、后圆盘结构参数都可以被确定下来，将通过实际算例，利用有限元方法对比分析改进前、后波发生器作用下，柔轮的变形和应力分布。

2 计算实例

2.1 算例参数

本文算例选自日本HD公司组件型CSF-90型号谐波齿轮减速器。其杯形柔轮剖面如图4所示，主要参数如表1所示。

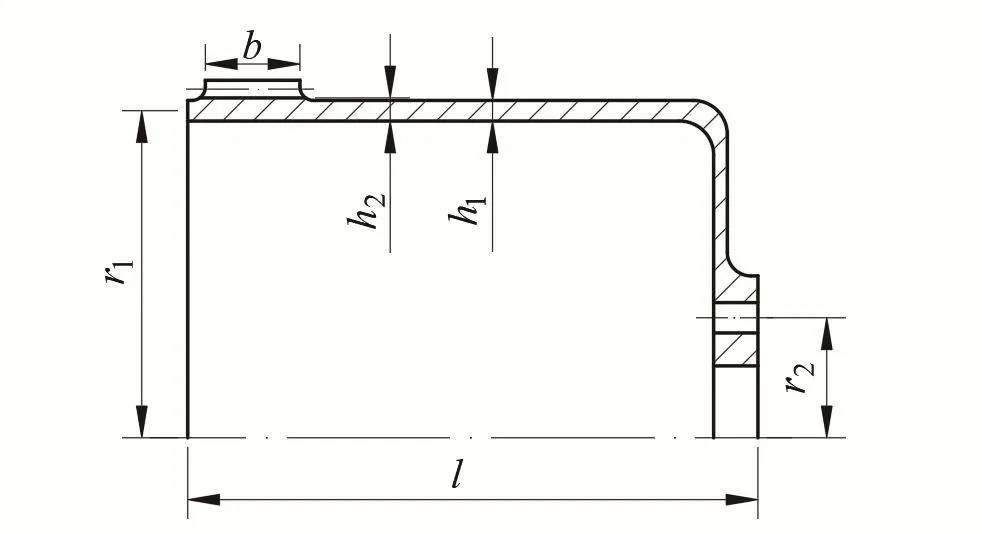
图4 柔轮结构剖面图

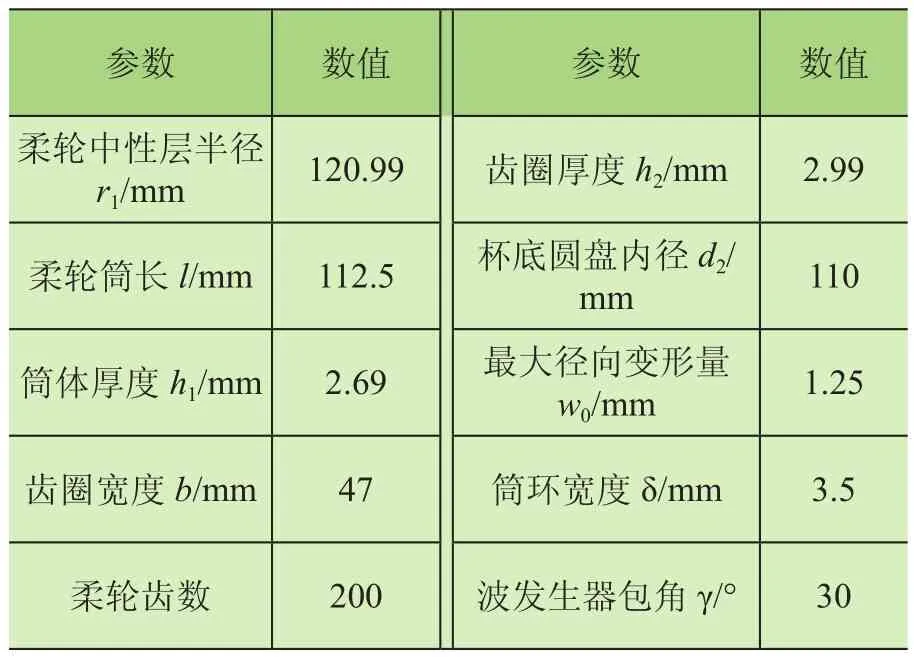
表1 CSF-90型号减速器主要参数

基于表1所示参数，根据1.2、1.3节理论分别计算出改进前、改进后两组波发生器结构参数。改进前圆盘计算半径R1= R2=118.006 m，偏心距e1= e2= 4.23 mm，波发生器与柔轮接触宽度bc为11.8 mm。改进后前盘计算半径R1=118.006 mm，偏心距e1=4.23 mm，后盘计算半径R2=118.50 mm，偏心距e2=3.51 mm，波发生器与柔轮接触宽度bc为11.8mm。

2.2 有限元模型建立

为提高工作效率和模型计算精度，本文选择基于APDL语言在Ansys环境中进行参数化建模，柔轮齿体部分选用Beam 44梁单元，通过定义实常数的形式来表现渐开线齿廓特征。建立柔轮筒体部分时，由于杯底圆台结构变形可以忽略，且对于柔轮变形几乎不产生影响，将其简化为筒体部分的边界条件。建立双圆盘波发生器时，由于本文暂不考虑柔性轴承的作用，将波发生器简化为2个对称的刚性圆面。波发生器及柔轮筒体均选用Shell 63壳体单元，该单元既具有弯曲能力又具有膜力，可以承受平面内载荷和法向载荷。

2.3 定义接触和施加约束

基于实际工况，定义波发生器与柔轮之间的面-面接触关系，波发生器外表面作为刚性目标面，定义Target 174单元，柔轮内壁作为柔性接触面，定义Contact 170单元。最后对有限元模型施加位移边界条件，选择波发生器外表面与柔轮杯底圆盘内孔的全部节点，对所选节点施加全约束。有限元装配模型如图5所示。

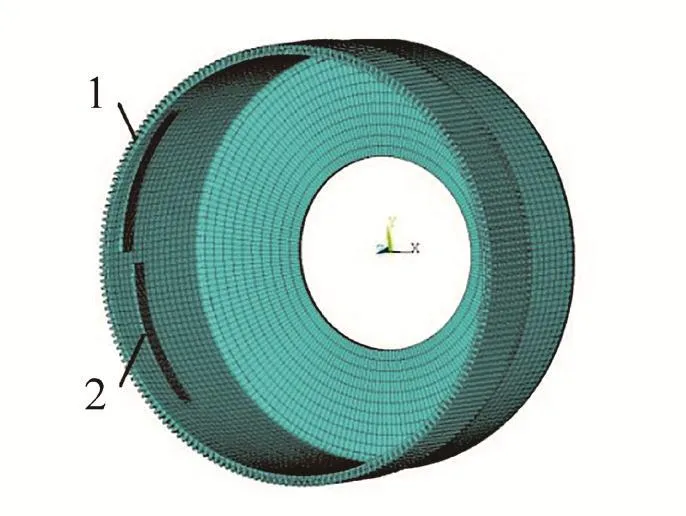
图5 有限元装配模型

2.4 模型有效性验证

将建立的有限元装配模型求解完成之后，对结果进行处理，显示柔轮整体径向位移分布如图6所示。柔轮整体径向位移云图呈对称分布，最大值出现在长轴齿圈前截面位置处，最小值出现在短轴位置，与柔轮的实际变形特征相一致。

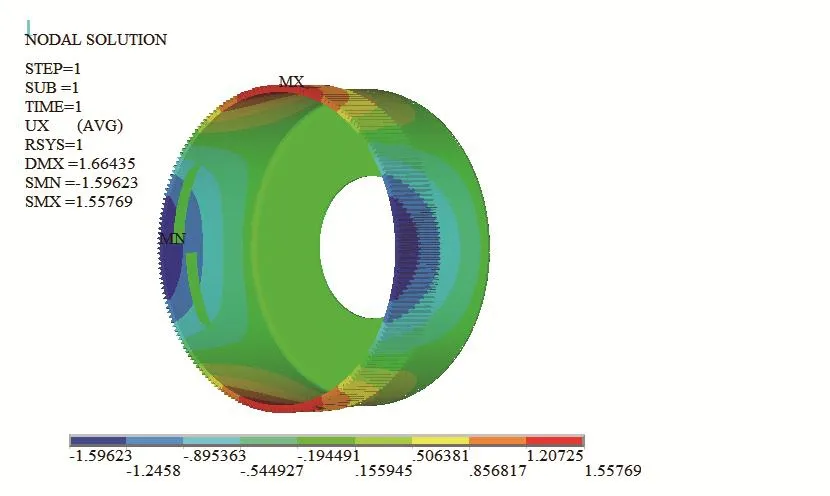
图6 柔轮径向位移分布云图

3 变形结果分析

基于求解后的两组有限元装配模型，定义路径分别提取前、后圆盘作用区间内柔轮中截面的变形结果，对比改进前与改进后的变形差异。

3.1 径向位移结果对比

图7所示为提取的两组有限元模型径向位移结果。横坐标表示极角坐标，φ=0°为长轴位置，顺时针为正，纵坐标表示径向位移量。 观察图7a可知，φ∈(0°，40°)区间内，两条径向位移曲线重合度较低，在φ=0°长轴位置处二者偏差最大，随着极角坐标增大，偏差逐渐减小。对比观察图7b，改进后波发生器作用下，两条径向位移曲线在整个区间范围内基本完全重合。对上述图7a、7b中前、后圆盘作用下径向位移曲线分别作差并进行对比分析，如图8所示。

图7 径向位移结果对比

图8所示为两组径向位移差值对比结果。可知改进前最大径向位移差值出现在长轴位置处，其值为236 um，相当于最大径向位移的19.2%，随着φ不断增大，差值呈现减小-增大-减小的趋势，变形特征不稳定。对于改进后，在整个区间范围内，径向位移差值曲线平稳，处于零线附近，最大差值出现在长轴位置处，其值为最大径向位移的1.2%。

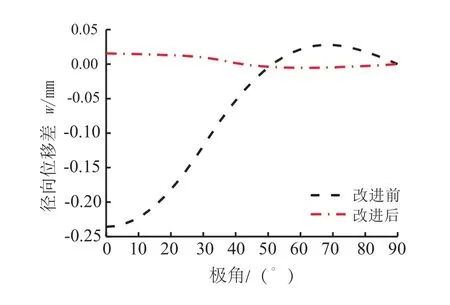
图8 径向位移差值结果对比

3.2 周向位移结果对比

图9a、9b为提取的两组有限元模型周向位移结果。观察图9a，柔轮在波发生器作用下产生变形时，由于后圆盘作用锥角较大，所以在整个区间内，后盘周向位移值大于前盘，且在φ∈(86°，90°)区间内，前盘周向位移为负值。对比观察图9b，在整个区间范围内，两条曲线非常重合，前、后圆盘作用下柔轮周向位移值基本完全相等，表明柔轮变形特征基本一致。

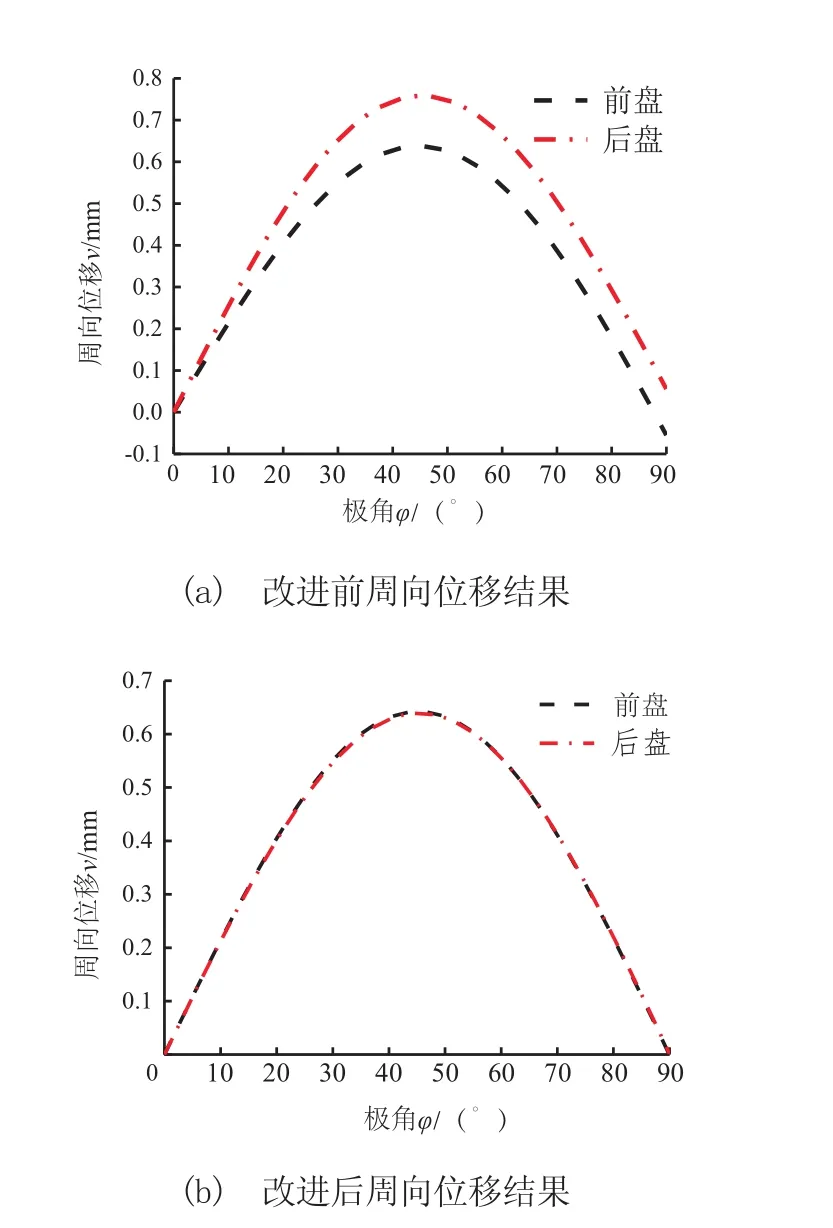
图9 周向位移结果对比

综上所述，通过对两组有限元模型径向位移和周向位移结果对比分析可得，在改进后双圆盘波发生器作用下，柔轮变形偏差相比改进前减小，一致性较高。

4 应力结果分析

柔轮在发生变形时，其包角位置处会出现应力集中现象，较高的应力会影响谐波减速器的承载能力和使用寿命。因此，定义路径提取第一、四象限范围内两组有限元模型等效应力和周向应力，对比结果如图10、图11所示。

如图10所示，φ=0°为坐标Y轴正向柔轮长轴位置，顺时针为正。在整个区间内，改进后柔轮筒体等效应力曲线低于改进前，在φ∈(90°，180°)后圆盘作用区间内，应力集中现象明显改善，其中在φ=150°位置处，改进后的应力值从102.11 MPa降低为87.16 MPa，降低了14.6%。

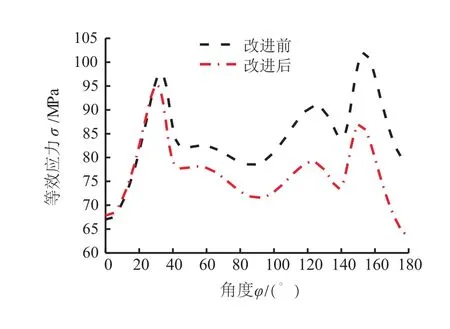
图10 等效应力结果对比

图11所示为周向应力结果对比图，从图中可以观察到，在φ∈(90°，180°)区间内，应力改善最为明显，其中，在φ∈(90°，135°)压应力区内，最大应力从-88.50 MPa降为-80.11 MPa，降低了9.5%。在φ∈(135°，180°)拉应力区间内，最大应力从89.39 MPa降为73.82 MPa，降低了17.4%。

图11 周向应力结果对比

综上所述，在改进后双圆盘波发生器作用下，柔轮齿圈最大应力相比改进前降低，其中，后圆盘作用区间内应力降低较为明显。

5 结论

1)基于柔轮直母线假定，以计算截面达到理论径向变形量为目标，提出了独立计算双圆盘波发生器前、后圆盘结构参数的方法。

2)相比于改进前，改进后波发生器前、后圆盘作用区间内，柔轮齿圈中截面径向和周向变形特征基本完全一致。

3)通过比较，改进后波发生器作用下，柔轮壳体上应力均存在降低，其中，后圆盘作用区间内，应力值降低最为明显，有助于提高柔轮的使用寿命。