蕴涵的决策蕴涵表示研究

王亚丽，翟岩慧,2+，张少霞，贾 楠，李德玉,2

1.山西大学 计算机与信息技术学院，太原 030006

2.山西大学 计算智能与中文信息处理教育部重点实验室，太原 030006

形式概念分析（formal concept analysis，FCA）是由德国Wille 教授于1982 年提出的一种通过形式背景建立概念格来对数据进行分析和提取规则的一个强有力的工具。它可以根据形式背景中对象和属性之间的相互关系来得到数据与数据之间隐含的概念并建立它们之间的代数结构，即概念格[1-2]。目前，FCA 已被广泛地应用到机器学习、社会网络、软件工程、信息检索、基于认知的概念学习、知识约简等相关领域[3-14]。

形式概念分析（概念格）中对知识获取的研究就是对蕴涵的研究[15-20]，但由于蕴涵数目庞大，无法满足用户的需求，因此如何获取完备无冗余的蕴涵规则集仍是研究的热点[16]。文献[16]从逻辑方面对完备性和无冗余性进行了讨论，其中Ganter等已经讨论了蕴涵的语义特征和语构特征，提出了三条蕴涵推理规则，而且证明了这三条推理规则相对于蕴涵的语义是完备的，并给出了源于文献[21]的一个蕴涵基（完备无冗余的蕴涵集合）。已经证明，该蕴涵基在所有蕴涵基中所含的蕴涵个数最少。Qu 等进一步讨论蕴涵和逻辑的关系，提出了一种新的蕴涵基，并给出一种有效的方法来生成该蕴涵基[22]。

为了减少蕴涵的数目，Qu 等提出了决策背景及决策蕴涵的概念[23]，并讨论了一种直观的推理规则（α推理规则），该推理规则通过增加决策蕴涵的前提或者减小决策蕴涵的结论来导出新的决策蕴涵[19]。文献[19]还讨论了基于该推理规则的完备性和冗余性，并提出了一种基于最小生成子[24]的决策蕴涵规范基生成算法。另外，文献[25]提出了一种基于真前提的决策蕴涵规范基生成算法，实验结果表明该算法效率更高。

研究发现，α推理规则在语构特征上并非是完备的，因此文献[23]提出了合并推理规则，并证明合并推理规则和α推理规则（扩增推理规则）是完备的推理规则集。在此基础上，文献[26]又给出一条新的推理规则——后件合并推理规则，它只对前件相同的决策蕴涵的后件进行合并。因此，后件合并推理规则在形式上更简洁。文献[26]也证明了扩增推理规则和后件合并推理规则是合理的、完备的并且是无冗余的。

此外，文献[27]给出了一个决策蕴涵基（称为决策蕴涵规范基）。该规范基基于决策前提[28]，即由决策前提作为该决策蕴涵集的前提，由决策前提相对于决策子背景的闭包作为该决策蕴涵集的结论。文献[27]还证明了该决策蕴涵规范基是完备的、无冗余的，并且在所有完备的决策蕴涵集中所含的决策蕴涵最少，因而决策蕴涵规范基是最精简的和最优的。研究结果表明，决策蕴涵规范基是蕴涵规范基[16]在决策背景下的对应概念，并且具有蕴涵规范基的所有优点。

事实上，决策蕴涵是一种特殊的蕴涵，因此，决策蕴涵的研究就是在蕴涵中建立并研究一个/多个封闭的子系统（包括决策蕴涵子系统及相应的语义和语构子系统），其中，不同的条件/决策属性划分决定了不同的封闭子系统。因此，蕴涵与决策蕴涵的研究本质上就是封闭系统与封闭子系统的研究。

本文将从语构方面深入研究由这些子系统（决策蕴涵）能不能得到整个系统（所有的蕴涵）。如果蕴涵可以由决策蕴涵推出，那么关于蕴涵的研究就可以转化为决策蕴涵的研究。这样就可以由决策蕴涵来生成蕴涵，甚至可以由决策蕴涵规范基生成蕴涵规范基。因此，蕴涵是否能由决策蕴涵表示是一个值得研究的问题。事实上，这种研究对于进一步厘清和发展蕴涵和决策蕴涵都是非常必要的。

1 FCA 基本概念

本章简要介绍形式概念分析中的一些基本概念。

定义1[16]形式背景是一个三元组K=(G,M,I)，其中G是对象集，M是属性集，I⊆G×M是对象和属性之间的二元关系。对于g∈G，m∈M，(g,m)∈I表示“对象g具有属性m”。

定义2[16]设K=(G,M,I)是一个形式背景，对于集合A⊆G，记：

相应地，对于集合B⊆M，记：

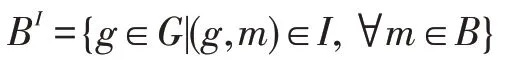
对于g∈G，为了简单起见，将{g}I记为gI。

定义3[16]设K=(G,M,I)是一个形式背景，对于集合A⊆G和B⊆M，若AI=B且BI=A，则称二元组(A,B)为形式概念，简称概念。其中A为该概念的外延，B为该概念的内涵。ℤ(K)称为K的所有概念的集合。

定义4[16]设K=(G,M,I)是一个形式背景，C1=(A1,B1)和C2=(A2,B2)是K的两个概念，定义偏序：

其中，C2是C1的超概念，C1是C2的子概念，所有概念在该偏序下构成格，称为概念格。

2 蕴涵

在形式概念分析中，属性之间的依赖可以通过蕴涵来描述。M中属性之间的蕴涵是M的一对子集，记为A→B，集合A是蕴涵A→B的前提，B是A→B的结论[16]。下面给出蕴涵相关的一些定义。

定义5[16]设K=(G,M,I)是一个形式背景，A,B⊆M，如果每一个具有属性集A的对象都具有属性集B，则A→B叫作形式背景K下的一个蕴涵。

定义6[16]设K=(G,M,I)是一个形式背景，T⊆M且A→B是形式背景K下的一个蕴涵。如果属性子集A⊈T或B⊆T，则称T是蕴涵A→B的一个模型，记为T╞(A→B)。设Θ为一蕴涵集，如果对每一个(A→B)∈Θ都有T╞(A→B)，则称T是Θ的一个模型，记为T╞Θ。

定义7[16]设K=(G,M,I)是一个形式背景，Θ为K的一个蕴涵集，若对于任意的T⊆M，T╞Θ蕴含T╞A→B，则称A→B可以从Θ语义导出，记为Θ├A→B。若任意的A→B∈Θ且(Θ(A→B))├(A→B)，则称A→B相对于Θ是冗余的。

定义8[16]设K=(G,M,I)是一个形式背景，Θ为K的一个蕴涵集，若对任意的A→B，Θ├A→B均成立，则称Θ是K的一个完备集。

以上是对蕴涵语义方面的研究，事实上，除了语义特征，蕴涵也有语构特征。通过蕴涵的语构特征，可以使用推理规则集从蕴涵集Θ导出新蕴涵[16]：

（1）X→X，X⊆M（自反性推理规则）；

（2）若X→Y∈Θ，则X⋃Z→Y∈Θ，X，Y，Z⊆M（增广性推理规则）；

（3）若X→Y∈Θ且Y⋃Z→W∈Θ，则X⋃Z→W∈Θ，W，X，Y，Z⊆M（伪传递性推理规则）。

文献[29]已经证明这三条推理规则相对于蕴涵的语义是完备的，即从Θ中导出的任意蕴涵都可以重复使用上述三条推理规则从Θ中推出。

3 决策蕴涵

决策蕴涵可以从两个角度进行研究：逻辑角度和数据角度。本章主要介绍决策蕴涵的逻辑研究，分为语义特征和语构特征两部分。

3.1 决策蕴涵的语义特征

首先给出决策背景及决策蕴涵的定义。

定义9[19]设K=(G,M,I)是一个形式背景，如果令M=C⋃D，I=IC⋃ID，其中C是条件属性集，D是决策属性集，C⋂D=∅，IC=G×C是条件关系，ID=G×D是决策关系，此时K=(G,C,D,I) 为一个以C为条件，D为决策的决策背景。反过来，如果以D为条件属性集，C为决策属性集，ID=G×D为条件关系，IC=G×C为决策关系，此时K=(G,D,C,I)是一个以D为条件，C为决策的决策背景。

定义10[19]设K=(G,C⋃D,IC⋃ID)是一个决策背景，对于集合A1⊆C，A2⊆D和B⊆G，记：

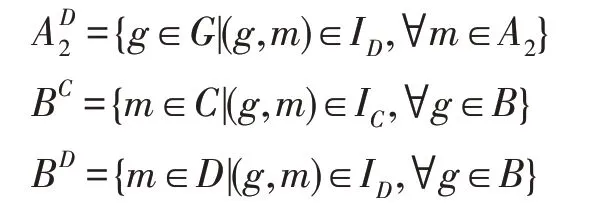
对于g∈G和A⊆C，将{g}C、{g}D和(AC)D简记为gC、gD和ACD。

定义11[19]设K=(G,C⋃D,IC⋃ID)是一个决策背景，若A⊆C且B⊆D，则称A→B是一个决策蕴涵。此时，A为该决策蕴涵的前提，B为该决策蕴涵的结论。

3.2 决策蕴涵的语构特征

本文只关注决策蕴涵的语构，语义方面的研究请参考文献[23]。

决策蕴涵的语构方面主要研究推理规则的合理性、完备性和无冗余性。文献[23]提出两条推理规则：

扩增推理规则：

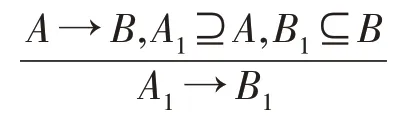
合并推理规则：

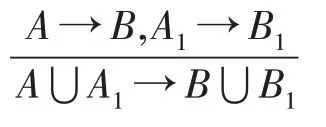
并且证明这两条推理规则是合理的、完备的且是无冗余的。

文献[26]在此基础上又提出了一条新的推理规则——后件合并推理规则：

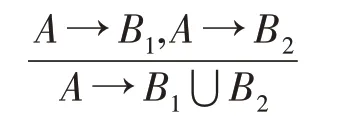
后件合并推理规则是一种特殊的合并推理规则，它只对前件相同的决策蕴涵的后件进行合并。因此，后件合并推理规则在形式上更简洁。文献[26]也证明了扩增推理规则和后件合并推理规则是合理的、完备的并且是无冗余的。

4 决策蕴涵表示蕴涵

首先从逻辑的角度来解释决策蕴涵表示蕴涵的含义。逻辑角度的分析可以从语义和语构两方面进行，为了简洁，本文主要使用语构的方式来分析这个问题。从语构上看，如果将决策蕴涵看作蕴涵的一个子系统，那么决策蕴涵可以表示蕴涵就意味着可以在一个/多个决策蕴涵集上应用蕴涵上的三条推理规则得出整个蕴涵系统。同时，因为决策蕴涵上的推理规则（简称决策推理规则）是蕴涵上推理规则（简称蕴涵推理规则）的特例，因此，使用决策推理规则可以推导出的蕴涵必然也可以使用蕴涵推理规则推导出。另一方面，蕴涵上的推理规则并不仅仅只有第2 章中描述的三条蕴涵推理规则，还可能存在其他的推理规则。但是，文献[29]已经证明这三条推理规则是完备的，因此在这里只考虑这三条推理规则；换句话说，如果蕴涵不能由这三条推理规则归结为决策蕴涵，那么其他推理规则也必然不能将蕴涵归结为决策蕴涵。

4.1 蕴涵表示的逻辑简化

为了使用决策蕴涵表示蕴涵，先引入下面的引理对需要表示的蕴涵进行简化。

引理1设A→B是形式背景K下的一个蕴涵，则蕴涵A→B成立，当且仅当∀bi∈B，A→bi均成立。

证明（必要性）因为bi∈B，所以有B={bi}⋃(B-{bi}) 。又因为A→B成立，所以A→{bi}⋃(B-{bi}) 。由自反性推理规则可知{bi}→{bi}成立，再由增广性推理规则可知{bi}⋃(B-{bi})→{bi}成立，最后由伪传递性推理规则及A→{bi}⋃(B-{bi})且{bi}⋃(B-{bi})→{bi}成立可知A→bi成立。

（充分性）先证明A→{b1}⋃{b2}成立。由自反性推理规则可知{b1}⋃{b2}→{b1}⋃{b2}成立，因为A→bi成立，由伪传递性推理规则及A→b1且{b1}⋃{b2}→{b1}⋃{b2} 成立可知A⋃{b2}→{b1}⋃{b2} 成立，即A→{b1}⋃{b2}成立，因为A⋃{b2}=A。接下来，令B1≜{b1}⋃{b2}，按照上述方法可证明A→B1⋃{b3}成立。以此类推，可证明A→B成立。

由引理1 可知，如果所有的A→bi均可由决策蕴涵表示，则A→B可由A→bi合并得出，因此也可由决策蕴涵表示，故只讨论后件中只有一个属性的蕴涵即可。

进一步，蕴涵的前件也可以被简化。

引理2设A→b是形式背景K下的一个蕴涵，A1⊆A。若A1→b成立，则A→b成立。

证明由增广性推理规则可知结论成立。

引理2 说明只要求出b成立的最小前件A1，就可以得到蕴涵A→b，因此，只要A1→b可由决策蕴涵表示，则A→b可由A1→b通过增广性推理规则得出，进而也可由决策蕴涵表示。故只讨论前件最小的蕴涵A→b即可。显然，此时有b∉A，因为A{b}→b成立当且仅当A{b}→b，这与A是最小前件矛盾。

综合引理1 和引理2 的结论可知，形如A→b(b∉A)的蕴涵可由决策蕴涵表示，则所有的蕴涵都可由决策蕴涵表示。

4.2 蕴涵表示的几种情况

接下来，具体分析形如A→b(b∉A)的蕴涵。

在形式背景K=(G,M,I) 中，如果令M=C⋃D，I=IC⋃ID，即K=(G,C⋃D,IC⋃ID)，则蕴涵A→b在K中存在六种情形：

（1）A⊆C，b∈D；

试验固定鲜花椒的添加量为 150 g，菜籽油添加量为 650 g，考察十三香添加量对“贡椒鱼”火锅品质的影响，结果见图2。

（2）A⊆D，b∈D；

（3）A⋂C≠∅，A⋂D≠∅，b∈D；

（4）A⊆C，b∈C；

（5）A⊆D，b∈C；

（6）A⋂C≠∅，A⋂D≠∅，b∈C。

情形（1）、（2）、（3）可综合表示为A2⋃A3→b，其中A2⊆C，A3⊆D，b∈D，A2⋃A3=A；情形（4）、（5）、（6）可综合表示为A2⋃A3→b，其中A2⊆C，A3⊆D，b∈C，A2⋃A3=A。

显然，情形（1）为K=(G,C,D,I)上的决策蕴涵，情形（5）为K=(G,D,C,I) 上的决策蕴涵；情形（2）为K=(G,D,I) 上的蕴涵，情形（4）为K=(G,C,I) 上的蕴涵。这说明，情形（1）和（5）已经归结为决策蕴涵；情形（2）和（4）已经归结为子背景上的蕴涵，因此可以按照后述方法，进一步将（2）和（4）归结为子背景上的决策蕴涵。

需要判断形如情形（3）和（6）的蕴涵是否能由决策蕴涵表示出来。在语义上，若形如情形（3）、（6）的蕴涵能由形如情形（1）、（2）、（4）、（5）的蕴涵通过蕴涵推理规则得出，则形如情形（3）、（6）的蕴涵是冗余的。另外，注意到互换情形（3）中C和D即可得到情形（6），反之亦然。这说明，如果情形（3）是冗余的，则情形（6）必然也是冗余的；如果情形（3）不是冗余的，需要一些特殊的方法才能生成，则互换方法中C和D，即可生成情形（6）的蕴涵。因此，只需考虑情形（3）即可。

现在考虑情形（3）中蕴涵A→b的表示。首先，有下面的结论。

引理3设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈D。如果A→b可以被决策蕴涵表示，则A→b最后一步必然是使用伪传递性推理规则推导出的。

证明如果A→b可以被表示，那么A→b必然是由三条蕴涵推理规则推导出来的。如果利用自反性推理规则，因为该推理规则具有自反性，显然不能说明A→b可以被决策蕴涵表示。因此，不能使用该推理规则推导出A→b。

对于增广性推理规则，若X⋃Z→Y可应用于A→b，则X⋃Z=A和Y={b}。由于A为能使蕴涵b成立的最小前件，因此对于任何N⊂A，N→{b}均不成立。显然，为了使推理规则有意义，Z≠∅，此时仍有X⊆A。当X⊂A时，X→{b}不成立，即不能由X→{b}得到A→b；当X=A时，X→{b}即为A→b，这表示A→b依赖于A→b。因此，增广性推理规则不能说明A→b可以被决策蕴涵表示，不能使用该推理规则推导出A→b。

下面考虑伪传递性推理规则。显然，如果A→b可以使用伪传递性推理规则推导出，则必有

成立。此时有X⋃Z=A。显然，当X→Y或Y⋃Z→b等于A→b时，该推理事实上是无效的。同时，若X→Y或Y⋃Z→b依赖于A→b时，则A→b也不能用伪传递性推理规则推导出；其中，X→Y依赖于A→b是指满足条件b∈Y且A⊆X，因为X→Y依赖于X→b，而X→b可由A→b使用增广性推理规则推得；类似地，Y⋃Z→b依赖于A→b是指A⊆Y⋃Z。进一步，有下面的结论。

定理1设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈D。A→b可以使用伪传递性推理规则推导出，当且仅当存在X,Y,Z⊆C⋃D，满足X≠∅，Y≠∅，b∉Y，Y⋃Z⊄A，A⊈Y⋃Z，X⋃Z=A且使式（1）成立。

证明（必要性）若X=∅，则Z=A，而要使∅→Y成立，Y只能为∅，从而Y⋃Z→b即 为A→b，因此X≠∅。

现证Y≠∅。由于A为能使蕴涵b成立的最小前件，因此对于任何N⊂A，N→{b}均不成立。由X⋃Z=A可知Z⊆A；当Z⊂A时Z→{b}不成立，为使Y⋃Z→b成立，有Y≠∅；当Z=A时，Z→{b}即为A→b，若Y=∅，则Y⋃Z→b即为A→b，这表示A→b依赖于A→b，因此A→b不能用伪传递性推理规则推导出，仍有Y≠∅。

现假设b∈Y，因为X→Y成立，由引理1 可知X→b成立。此时，由X⋃Z=A可 知X⊆A，因 为X⋃Z为能使蕴涵X⋃Z→b成立的最小前件，所以，当X⊂A时X→b不成立，矛盾；当X=A时，X→b即为A→b，因此X→Y依赖于A→b，这表示A→b不能用伪传递性推理规则推导出。因此有b∉Y。

现假设Y⋃Z⊂A。因为A为能使蕴涵A→b成立的最小前件，所以，当Y⋃Z⊂A时Y⋃Z→b不成立，矛盾。因此有Y⋃Z⊄A。

现假设A⊆Y⋃Z，由增广性推理规则可知，Y⋃Z→b可以由A→b推得，这表示Y⋃Z→b依赖于A→b。因此有A⊈Y⋃Z。

（充分性）因为A为能使蕴涵A→b成立的最小前件，所以对于任何N⊂A，N→{b} 均不成立，Y⋃Z⊄A保证了Y⋃Z→b的可成立性。由题设可知，为证明A→b可以使用伪传递性推理规则推导出，只需证X→Y和Y⋃Z→b不等于且不依赖 于A→b即可。

由b∉Y可知X→Y不等于且不依赖于A→b。

由A⊈Y⋃Z可知，Y⋃Z→b不等于且不依赖于A→b。

在定理1 中，因为X,Y,Z⊆C⋃D，所以X→Y和Y⋃Z→b均可能属于情形（3）或情形（6），换句话说，情形（3）又依赖于情形（3）或情形（6）。因此，可将定理1 进一步分为两种情况：一种情况是可以使用伪传递性推理规则由情形（1）、（2）、（4）、（5）推导出情形（3），称为直接表示；另一种情况是情形（3）必须依赖于情形（3）或（6）才能推导出，称为间接表示。

由于蕴涵推理的复杂性，目前暂未发现需要间接表示的蕴涵，因此本文只考虑直接表示。首先给出直接表示A→b的判定条件。

定理2设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈D。A→b可以使用伪传递性推理规则直接表示当且仅当存在X≠∅，Y≠∅，b∉Y，Y⋃Z⊄A，A⊈Y⋃Z，X⋃Z=A且满足以下条件之一：

（1）X=A2，Z=A3，且存在Y⊆D使式（1）成立；

（2）X=A3，Z=A2，且存在Y⊆C使式（1）成立。

证明根据题设，A→b属于情形（3）中的蕴涵。

（必要性）若情形（3）中A→b可以使用伪传递性推理规则直接表示，则必满足定理1 所给条件；进一步，X→Y和Y⋃Z→b均不属于情形（3）或（6）的蕴涵。因此，X必不满足X⋂C≠∅且X⋂D≠∅，Z必不满足Z⋂C≠∅且Z⋂D≠∅，此时有X=A2,Z=A3或X=A3,Z=A2。当X=A2,Z=A3时，X→Y必不属于情形（3）或（6），Y⋃Z→b不属于情形（3）或（6）时Y需满足Y⋂C=∅，即Y⊆D；当X=A3,Z=A2时，X→Y必不属于情形（3）或（6），Y⋃Z→b不属于情形（3）或（6）时Y需满足Y⋂D=∅，即Y⊆C。

（充分性）由假设和定理1 可知，A→b可以使用伪传递性推理规则表示。

现分别假设条件（1）、（2）成立时来证X→Y和Y⋃Z→b必不属于或依赖于情形（3）或（6）。

（1）当X=A2，Z=A3且存在Y⊆D时，显然，X→Y属于情形（1），Y⋃Z→b属于情形（2）。

（2）当X=A3，Z=A2且存在Y⊆C时，显然，X→Y属于情形（5），Y⋃Z→b属于情形（1）。

定理1 虽然给出了情形（3）中A→b冗余的充要条件，但仍不能确定情形（3）的冗余性。下面给出一个例子，来说明情形（3）不是冗余的，换句话说，存在情形（3）所示的蕴涵不能被决策蕴涵表示。

例1一个决策背景如表1 所示，其中{x1,x2,x3,x4}代表4个对象，{a}是条件属性集，{b,d}是决策属性集。

Table 1 Decision context表1 决策背景

显然，{a}⋃{d}→b是该决策背景的蕴涵，令A2{a}，A3{d}，则{a}⋃{d}→b属于情形（3）。接下来，利用伪传递性推理规则来推导该蕴涵。由定理1，首先假设X≠∅，Y≠∅。

首先考虑Z=∅的情况。此时，需要找到Y使

成立。Y所有可能的取值为{a,b,d,ab,ad,bd,abd} 。当Y取{a,d}中的任意一个时，Y→b均不成立；当Y取{b,ab,ad,bd,abd}中的任意一个时，用到{a}⋃{d}→b本身。因此，当Z=∅时，不存在Y使{a}⋃{d}→b可以由其他蕴涵推导出，即{a}⋃{d}→b不冗余。

接下来考虑Z≠∅的情况。此时需要找到Y使

成立。Y所有可能的取值为{a,b,d,ab,ad,bd,abd} 。当Y取{b,d,ab,ad,bd,abd}中的任意一个时，{a}→Y不成立；当Y取{ }a时，用到{a}⋃{d}→b本身。类似地，当Y取{a,b,ab,ad,bd,abd}中的任意一个时，{d}→Y不成立；当Y取{d} 时，Y⋃{a}→b不成立。因此，当Z≠∅时，不存在Y使{a}⋃{d}→b可以由其他蕴涵推导出，即{a}⋃{d}→b不冗余。

4.3 蕴涵表示的具体方法

例1 表明，某些蕴涵确实不可直接归结为决策蕴涵和子背景的蕴涵。因此，需找到蕴涵不可以被直接表示时Y应满足的条件，并生成相应的蕴涵。为此，首先讨论决策属性只有一个属性的情形下，Y存在或不存在的情况。有下面的结论。

引理4设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈D。若决策属性D中只有一个属性，则A→b是冗余的。

证明根据题设，A→b属于情形（3）中的蕴涵。若决策属性D中只有一个属性，由于b∈D，因此有A3={b}，故A→b是冗余的。事实上，由自反性推理规则可知{b}→b成立，再由增广性推理规则可知A→b成立。

接下来，分析当决策属性D中只有一个属性时，情形（6）中的蕴涵是否可以被直接表示。基于该情形的分析，可以将形式背景分为只含有一个决策属性的决策背景，然后生成该决策背景中的决策蕴涵，因为情形（3）的蕴涵是冗余的，因此不需要生成，如果情形（6）中的蕴涵是不可以被直接表示的，则可以生成不可以被直接表示的蕴涵；接下来，就可以考虑去掉该决策属性之后的形式背景；以此类推，可以生成所有的蕴涵集。

容易证明，定理1、定理2对于情形（6）也是成立的。

推论1设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈C。A→b可以使用伪传递性推理规则推导出，当且仅当存在X,Y,Z⊆C⋃D，满足X≠∅，Y≠∅，b∉Y，Y⋃Z⊄A，A⊈Y⋃Z，X⋃Z=A且使式（1）成立。

推论2设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈C。A→b可以使用伪传递性推理规则直接表示当且仅当存在X≠∅，Y≠∅，b∉Y，Y⋃Z⊄A，A⊈Y⋃Z，X⋃Z=A且满足以下条件之一：

（1）X=A2，Z=A3，且存在Y⊆D使式（1）成立；

（2）X=A3，Z=A2，且存在Y⊆C使式（1）成立。

下面的例子表明，当决策属性D中只有一个属性时，对于推论2 所示的两种情况，情形（6）中的蕴涵不总是可以被直接表示的。

例2对于表1 中的决策背景，令{a,b}是条件属性集，{d} 是决策属性集，则{a}⋃{d}→b为蕴涵。令A2≜{a}，A3≜{d}，则{a}⋃{d}→b属于情形（6）。接下来，利用伪传递性推理规则来推导该蕴涵。

首先考虑推论2 中（1）。此时，需要找到Y⊆D使式（1）成立。由表1 可知Y只能取{d}，由{d}→b不成立可知{a}⋃{d}→b不可以被直接表示。

接下来考虑推论2 中（2）。此时，需要找到Y⊆C使式（1）成立。Y所有可能的取值为{a,b,ab}。无论Y取何值，{d}→Y均不成立，因此{a}⋃{d}→b不可以被直接表示。

由例2 可知，需找出当决策属性D中只有一个属性时，对于推论2 所示的两种情况，情形（6）中的蕴涵A→b不可以被直接表示的充要条件及发现算法。

对于推论2 中（1），有下面的结论。

引理5设K=(G,C⋃D,IC⋃ID)是一个决策背景，A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈C。若决策属性D中只有一个属性，则X=A2，Z=A3，Y⊆D时，A→b不可以被直接表示。

证明当D中只有一个属性d时，由Y≠∅和Y⊆D可 知Y={d}，由Z=A3⊆D可 知Z={d}，由A⋂D≠∅和A⋂C≠∅可知Y⋃Z⊂A，再由A为能使蕴涵b成立的最小前件可知Y⋃Z→b不成立，从而A→b必不可以被直接表示。

由引理5 可知，当决策属性D中只有一个属性时，对于推论2 中（1），情形（6）中的蕴涵A→b是不可以被直接表示的，由于A→b可以被直接表示时只需满足推论2 条件之一，因此，若对于推论2 中（2），A→b也不可以被直接表示，那么情形（6）中的蕴涵A→b必不可以被直接表示。接下来给出对于推论2中（2）情形（6）中的蕴涵A→b也不可以被直接表示的判定条件。

定理3设K=(G,C⋃D,IC⋃ID)是一个决策背景且D中只有一个属性d。A→b是K上的一个蕴涵，其中A⋂C≠∅，A⋂D≠∅，b∈C。蕴涵A→b不可以被直接表示，当且仅当任意的Y⊆C均满足以下条件之一：

（1）Y=∅；

（2）b∈Y；

（3）Y⋃A2⊂A；

（4）A⊆Y⋃A2；

（5）存在g满足gD={d}且Y⊈gC；

（6）存在g满足(Y⋃A2)⊆gC且b∉gC。

其中A=A3⋃A2,A3⊆D,A2⊆C,b∈C,g∈G。

证明根据题设，A→b属于情形（6）中的蕴涵。由推论2 可知，情形（6）中的蕴涵A→b不可以被直接表示当且仅当条件（1）～（4）之一成立或推论2 中（1）和（2）皆不成立。若D中只有一个属性d时，由引理5 可知，推论2 中（1）必不成立；因此，若D中只有一个属性d时，情形（6）中的蕴涵A→b不可以被直接表示当且仅当条件（1）～（4）之一成立或推论2 中（2）不成立。现只需证推论2 中（2）不成立当且仅当条件（5）或（6）成立即可。

因为D中只有一个属性d，所以A3={d}。因此，只需证不存在Y⊆C使式（2）成立

当且仅当条件（5）或（6）成立。这是显然的，因为不存在Y⊆C使式（2）成立当且仅当不存在Y⊆C使{d}→Y或Y⋃A2→b成立，当且仅当（存在g满足gD={d}且Y⊈gC）或（存在g满足(Y⋃A2)⊆gC且b∉gC），当且仅当条件（5）或（6）成立。

当D中只有一个属性d时，由引理5 可知，情形（3）中的蕴涵都是冗余的，因此不必生成；对于情形（6），定理3 事实上给出了不可被直接表示的蕴涵的生成方法。

对于形式背景K=(G,M,I)，令D={d}，C=MD，I=IC⋃ID，即得到只含一个决策属性的决策背景KC|D=(G,C⋃D,IC⋃ID)和只含一个条件属性的决策背景KD|C=(G,D⋃C,ID⋃IC)。生成形式背景K的具体步骤如下：

（1）生成决策背景KC|D的决策蕴涵。

（2）生成决策背景KD|C的决策蕴涵。

（3）生成K不可被直接表示的蕴涵：

①对于任意的A2⊆C和任意的b∈C执行②和③。

②令A3={d}⊆D，A=A3⋃A2，根据定理3检查是否存在Y⊆C满足定理3 条件（1）～（6）之一。若满足，则执行步骤③，否则执行①。

③判断A→b是否成立。若成立，则生成蕴涵A→b。

（4）从K中移除属性d，并记Kd=(G,M{d},II{}d)，对Kd重新执行该算法。

显然，上述算法的复杂度较高，因此难以应用于具体的数据集中。

5 结论与展望

本文首先对蕴涵进行了逻辑简化，然后使用蕴涵推理规则研究蕴涵是否可以由决策蕴涵表示，首先给出了蕴涵可以被直接表示时应满足的条件。实例表明，不是所有的蕴涵都可以直接归结为决策蕴涵，因此找出了不可以直接归结为决策蕴涵的蕴涵应满足的充要条件，并给出了不可以直接归结为决策蕴涵的蕴涵的生成方法。

文中提到了蕴涵的间接表示，但由于蕴涵推理的复杂性，暂未对其进行深入研究。另外，即使不能被直接表示的蕴涵的生成算法也有较大的复杂度，因此难以应用于具体的数据。这些都是下一步需要研究的问题。

另外可以发现，存在一些蕴涵可以由决策蕴涵表示，那么决策蕴涵规范基与蕴涵规范基、决策蕴涵推理规则与蕴涵推理规则以及决策背景上的概念格与形式背景上的概念格之间又存在怎样的联系?进一步，本文的研究是否可以推广到模糊决策蕴涵[17-18，30]以及可变决策蕴涵[31]？这些问题也是接下来需要研究的。