改进混合二进制蝗虫优化特征选择算法

赵泽渊，代永强

甘肃农业大学 信息科学技术学院，兰州 730070

特征选择（feature selection）是从数据集已有的N个特征中去除冗余、无用的特征，并选出具有M个特征的特征子集的方法（M≤N），该方法能够降低特征数目，提高分类算法的分类性能[1]。

常见的特征选择方法分为过滤式（filter）、封装式（wrapper）、嵌入式（embedded）[2-3]。过滤式方法与特定的学习算法无关，该方法从数据集本身的内在性质（如相关性）获得评价标准，然后根据各子集的优劣进行选择[4]。封装式方法是从数据集中不断产生特征子集并将其用来训练分类器，最后根据分类器的性能来选择最优特征子集[5]。而在嵌入式方法中，特征选择算法本身作为组成部分嵌入到分类算法里[4]。封装式方法直接面向算法优化，易于实现，并且精度与鲁棒性优于过滤式与嵌入式方法，因此本文采用封装式的方法进行特征选择。

假设数据集维度为n，穷举搜索最优特征子集的时间复杂度为O(2n)，对高维度数据进行特征选择时使用穷举搜索需要耗费大量时间以及计算资源[6-7]。启发式搜索最优特征子集是通过对比特征子集增减特征前后的优劣程度来搜索最优特征子集，其时间复杂度为O(n2)。虽然启发式搜索方法在高维度条件下的性能优于穷举搜索方法，但其仍然需要花费大量时间成本。随机搜索是指将特征选择与随机优化算法相结合，使用随机优化算法的优化策略生成子集，并使用特定的评价函数来评价子集的优劣，最后依照自定义的结束条件来完成特征子集的选择。对于高维度数据的特征选择问题来说，随机搜索方法的效率远远高于穷举搜索方法和启发式搜索方法。在随机搜索方法中，随机优化算法的性能很大程度上决定了特征子集搜索方法的性能。

近年来，随机优化算法得到了科研工作者的广泛关注[8-10]，相关学者对遗传算法（genetic algorithm，GA）[11]、蚁群算法（ant colony optimization，ACO）[12]、人工蜂群算法（artificial bee colony，ABC）和粒子群优化算法（particle swarm optimization，PSO）[13]等随机优化算法进行了深入和系统的研究，并将这些算法用于特征选择问题的求解。

受蝗虫种群行为启发，Saremi等[14]于2017年提出了蝗虫优化算法（grasshopper optimization algorithm，GOA）。该算法原理简单易懂，易于实现，并且能够在小空间内搜索时保持搜索个体均匀分布，限制个体重合，因此相较于其他群智能算法，该算法具有较好的局部搜索性能，有利于优化特征选择算法的局部搜索能力。近年来对GOA 的研究内容包括改进与应用两方面。Tumuluru 等[15]提出了一种利用基因表达数据进行癌症分级的方法，并利用GOA 优化了该方法中深度置信神经网络的权值，实验结果表明该方法的分级结果具有较高的准确率；Mafarja 等[16]提出了一种基于GOA、选择算子和进化种群动力学（evolutionary population dynamics，EPD）的特征选择算法，并与其他同类方法进行了对比实验，结果表明该算法的性能优于文献中的其他算法；Liao 等[17]提出了一种基于邻域质心的蝗虫优化算法，实验结果表明改进算法具有更高的种群多样性与收敛精度；Fathy[18]提出了一种基于GOA 的光伏阵列最优重构过程的求解方法，并通过实验证实了该方法的可靠性和有效性；Lal 等[19]设计了一种混合动力系统的分数阶模糊PID（proportion integration differentiation）频率控制器，利用GOA 优化了该频率控制器的参数，并通过实验证实了该控制器的有效性；闫旭等[20]利用量子旋转门操作改进了GOA，提出了一种基于量子计算思想的混合蝗虫优化算法，并利用作业车间标准测试问题进行了仿真实验，结果表明该算法对比文献中的其他四种算法具有更好的性能；李洋州等[21]通过引入曲线自适应与模拟退火算法提高GOA 的收敛速度与精度，提出一种曲线自适应和模拟退火蝗虫优化算法，实验结果表明该算法比改进前的算法具有更好的求解质量与收敛速度。上述文献说明GOA 能够在各类优化问题中表现出较优的性能，但其自身存在全局搜索性能弱与收敛精度低的不足，算法性能有较大的提升空间。

1 基本蝗虫优化算法

蝗虫优化算法[14]是受蝗虫种群行为启发而提出的群智能算法。经过研究蝗虫群体迁移、聚集、觅食的行为发现，蝗虫个体在群体中会受到种群交互力、重力和风力的影响。基于模拟蝗虫群体行为的数学模型如式（1）～（4）[14]：

其中，Xi表示第i只蝗虫的位置，Si、Gi、Ai分别表示第i只蝗虫受到的种群交互力、重力和风力。

式（3）为s函数的表达式，用于计算蝗虫个体间的吸引力与排斥力：s(r)>0，蝗虫个体间相互吸引，则称r的取值范围为吸引域；s(r)<0，蝗虫个体间相互排斥，则称r的取值范围为排斥域；s(r)=0，蝗虫个体间既不吸引也不排斥，则称r的取值为舒适距离（注意当r的取值过大时，s(r)趋近于0，但这时r的取值并非是舒适距离。Saremi 等[14]指出，将蝗虫个体间的距离限制在[1,4]上可以避免蝗虫间距离过大对算法产生的不利影响）。式（3）中f为吸引强度参数，l为吸引尺度参数，通过改变两者的取值情况可以控制蝗虫之间的吸引域、排斥域和舒适距离的分布情况和吸引与排斥的强度。参考Saremi 等[14]对两者的取值，本文取l=1.5，f=0.5。

结合上述公式，通常使用下式进行优化问题的求解：

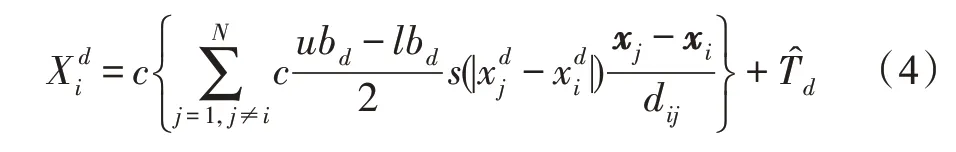
综上可知，蝗虫个体的位置不仅受到目标位置的影响，还会受到其他所有个体位置的影响。在种群向目标位置收敛的过程中，蝗虫个体受到种群交互力的影响，搜索范围、个体间的舒适距离不断减小，但个体之间仍保持一定的间距，在一定范围内分散地搜索，最终所有蝗虫个体会均匀分布到目标位置附近。这种搜索个体之间的独特交互方式，是蝗虫优化算法的显著特征，使得蝗虫优化算法具备了较好的局部开发能力。

2 改进的混合二进制蝗虫优化特征选择算法

本文通过改进二进制转化策略并引入混合复杂进化方法，进一步提高了二进制蝗虫优化特征选择算法的性能。通过对UCI数据集进行特征选择，实验结果表明，改进算法获得了更好的特征子集，取得了更好的分类效果。

2.1 基本二进制蝗虫优化特征选择算法

2.1.1 基本二进制蝗虫优化算法

蝗虫优化算法独特的进化方式与较好的局部开发能力，使其在连续的优化问题中拥有较好的性能。为了利用蝗虫优化算法产生特征子集，需要对其进行离散化处理。GOA 经过对种群初始化和更新策略的修改后可得到二进制蝗虫优化算法（binary grasshopper optimization algorithm，BGOA）[16]，具体方法如下：

（1）种群初始化

在特征选择算法中，每个蝗虫个体代表一个解，其位置信息表示特征的选取情况。使用下式对初始蝗虫种群进行二进制赋值[16]：

（2）更新策略

其中，本文引入了系数A来控制横轴伸缩度，T(x)函数的返回结果为该个体d维位置变化概率。

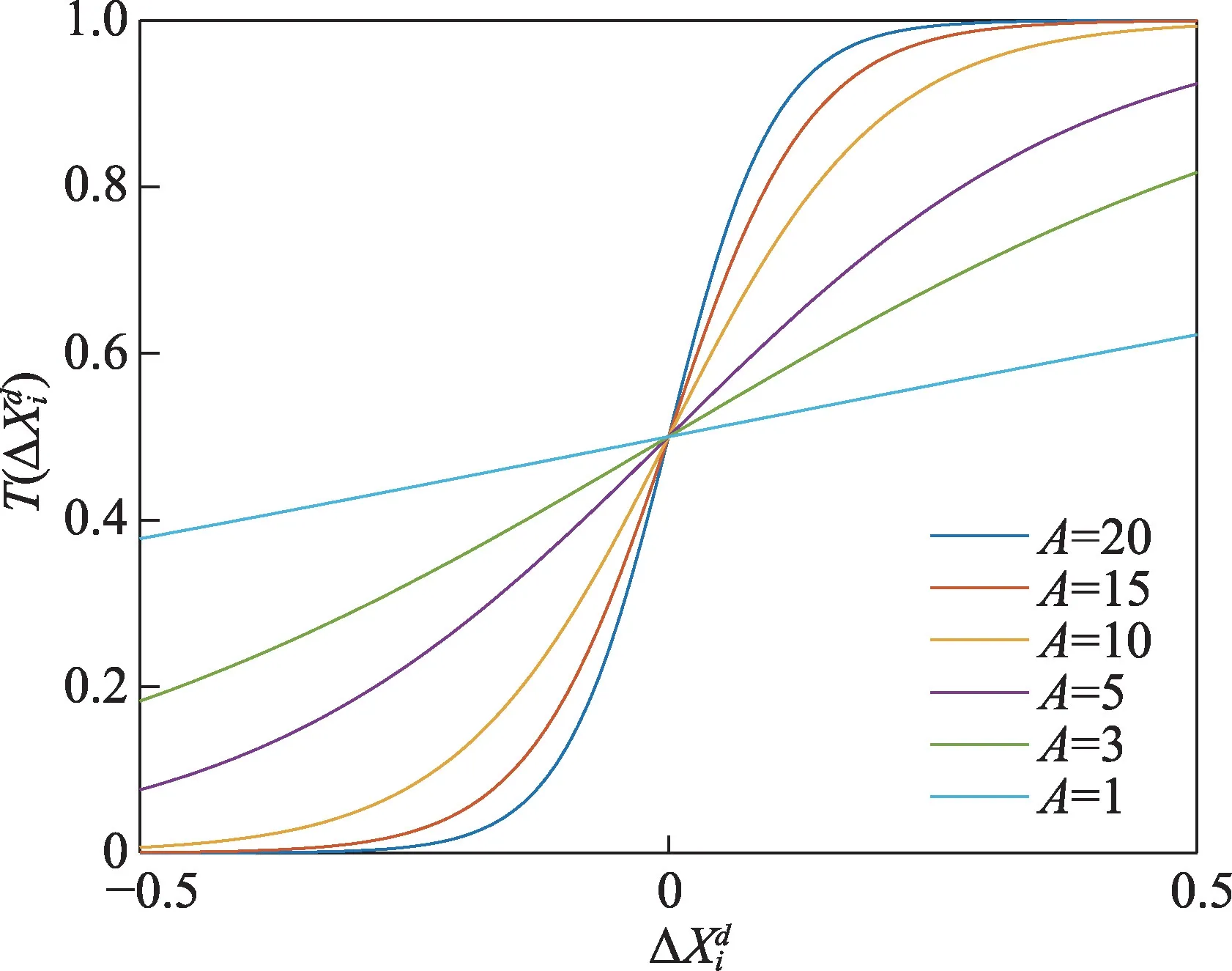
Fig.1 Image of T(x) function图1 T(x)函数图像

最后，使用式（8）得出更新后蝗虫个体的位置[16]。

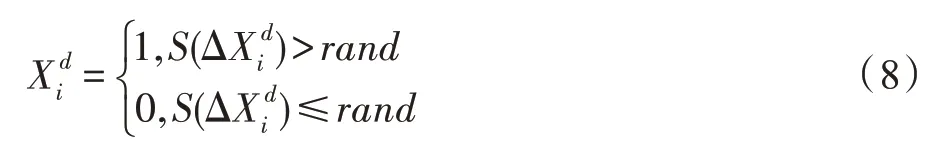
其中，rand为(0,1)上的随机数。

2.1.2 特征选择实现流程

基于BGOA 的特征选择算法伪代码如下所示。

初始化BOGA 特征选择算法参数cmax、cmin、最大迭代次数Tmax

初始化数据集、数据集参数

按照2.1.1 小节的方法进行种群初始化，同时使用特征子集评价函数（见2.4 节）计算所有个体的适应度

首先利用BGOA 产生二进制个体，依照每个个体的编码选取特征子集，之后使用特征子集评价函数对每个个体所对应的特征子集进行评价，最后依据评价结果更新各个个体。依照上述流程不断循环，直至达到最大迭代次数Tmax，此时将适应度最低的个体作为结果返回。

时间复杂度分析：BGOA 中个体更新需要计算其他所有个体的位置，假设个体数量为N，则单个个体更新一次的时间复杂度为O(N)，群体更新一次的时间复杂度为O(N2)；假设最大迭代次数为Tmax，则可以得出BGOA特征选择算法的时间复杂度为O(N2×Tmax)。

2.2 改进二进制蝗虫优化特征选择算法

BGOA 特征选择算法的二进制转化方式具有过大的随机性，导致蝗虫个体更新较为盲目，在高维度条件下性能不佳。为了降低BGOA 特征选择算法更新的盲目性，增强探索能力，提高维度条件下的性能，本文引入了步长引导个体位置变化的二进制转化策略替代BGOA 特征选择算法原有的转化策略。将改进后的算法称为改进二进制蝗虫优化算法（improved binary grasshopper optimization algorithm，IBGOA）特征选择方法。

2.2.1 改进策略

本文提出了一种步长引导个体位置变化的二进制转化策略，该策略如下所述：

首先，根据式（6），可以将式（4）改写为：

为了使二进制化后的蝗虫个体能够根据步长大小控制更新后的位置与目标位置之间的距离，本文基于Sigmoid 函数提出了新的函数S(x)对步长进行转化，S(x)如式（10）所示。

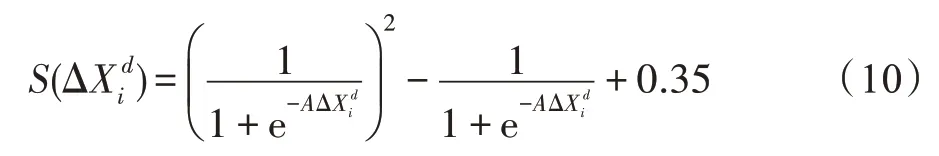
其中，A为系数，用来控制横轴伸缩度，S(x)函数的返回结果为个体d维位置变化概率。

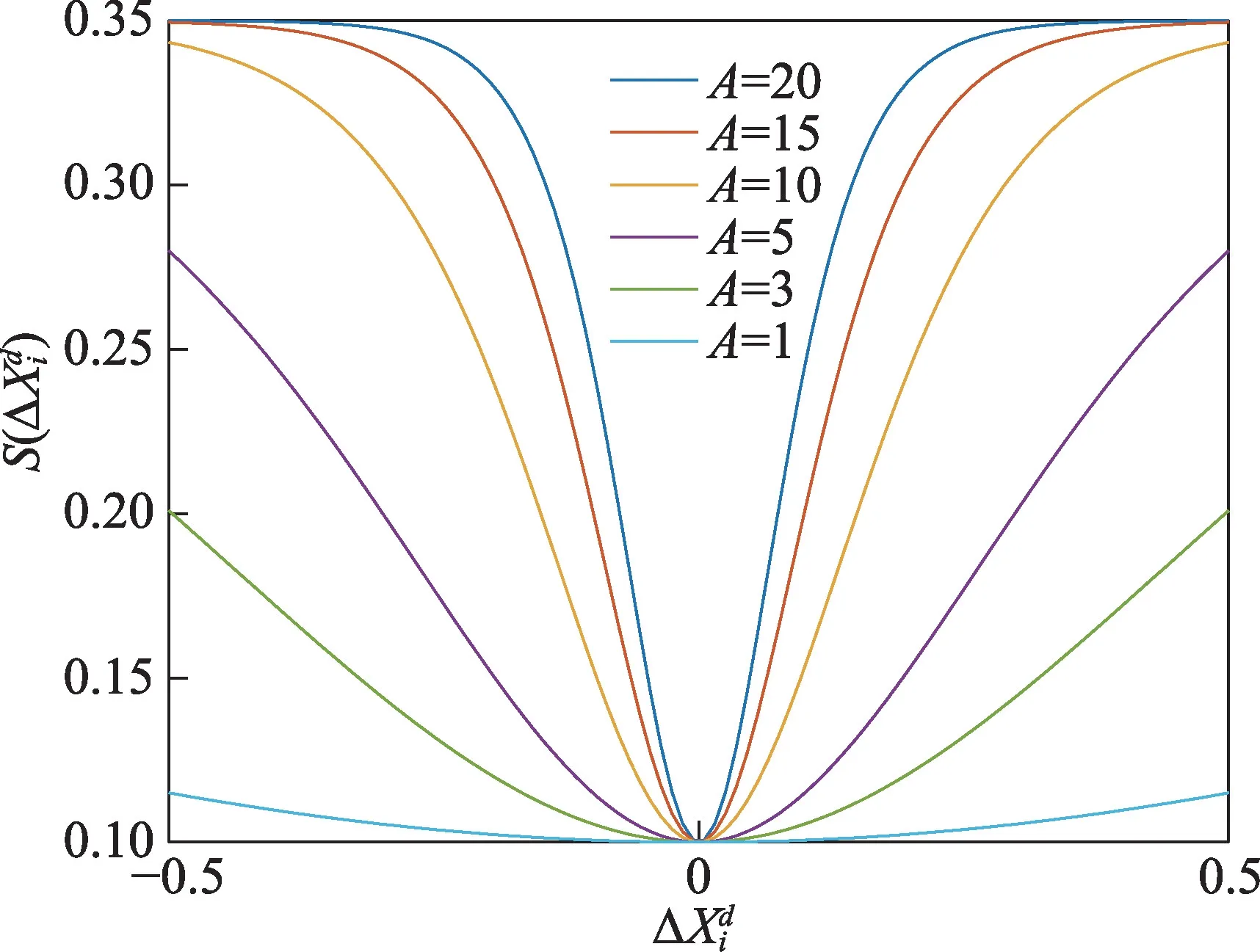
Fig.2 Image of S(x) function图2 S(x)函数图像

根据转换函数计算出当前蝗虫个体每一维度上的变化概率之后，使用式（11）对S(ΔXdi)进行转化：

综上可知，IBGOA 特征选择算法中蝗虫个体基于其受到的种群交互力得到位置变化概率，然后基于位置变化概率与目标位置得出新的位置。相比于BGOA 特征选择算法，IBGOA 特征选择算法个体的更新方式具有更好的目的性和探索性能。

2.2.2 改进策略性能验证

为验证新的二进制转化策略的性能，本文设计了一种验证实验方案，比较采用两种改进更新策略后算法的性能，实验步骤如下：

（1）按照2.1.1 小节的方法初始化一个蝗虫种群，并将第一个蝗虫个体作为目标个体。

（2）分别采用改进前后的两种二进制转化策略对蝗虫种群进行一次更新，得到更新后的两个蝗虫种群。

（3）对于更新前后的三个蝗虫种群，分别计算其群体中两两蝗虫之间的距离，并计算所有蝗虫之间的平均距离dis。

本文按照上述的实验方案分别在c=cmax=1 和c=cmin=0.000 01 两个条件下进行了10 次独立重复实验，其中蝗虫个体数量N=80，维度dim=10。10 次实验中dis的平均值如表1 所示。

Table 1 Experimental results of average distance dis表1 平均距离dis 实验结果

参数c用于平衡算法的全局探索能力与局部搜索能力。c=cmax=1 时，算法处于全局探索阶段，观察表1 可知，采用两种策略更新后的蝗虫群体中个体之间的平均距离相较于更新前均有所增加，但是采用新策略更新后的蝗虫群体中个体之间的平均距离增加更为明显，说明采用新策略的算法前期的探索能力更强。c=cmin=0.000 01 时，算法处于局部搜索阶段，观察表1 可知，采用新策略更新后的蝗虫群体中蝗虫个体之间的平均距离相较于更新前有明显缩减，旧策略反而增加，说明采用旧策略的算法后期的局部搜索过程具有盲目性，而采用新策略的算法收敛性更强，更具有目的性。综上所述，相较于基本算法的二进制转化策略，本文提出的步长引导个体位置变化的二进制转化策略对算法前期的探索能力与后期的收敛性能均有提升。

2.2.3 特征选择实现流程

IBGOA 特征选择算法的伪代码如下所示。

初始化IBGOA 特征选择算法参数cmax、cmin、最大迭代次数Tmax

初始化数据集、数据集参数

按照2.1.1 小节的方法进行种群初始化，同时使用特征子集评价函数（见2.4 节）计算所有个体的适应度

相较于BGOA 特征选择算法，该算法只对个体更新公式进行了调整，整体流程并无变化；由于IBGOA 特征选择算法在个体更新时需要额外计算一个公式，因此该算法的时间复杂度可以表示为O(N×(N+1)×Tmax)=O(N2×Tmax)，而BGOA 特征选择算法的时间复杂度也为O(N2×Tmax)，因此两者差异可以忽略不计。

2.3 混合二进制蝗虫优化特征选择算法

IBGOA 特征选择算法在局部搜索中具有良好的性能，但其全局搜索能力较差，容易陷入局部最优。本文在IBGOA 特征选择算法中引入了混合复杂进化方法（shuffled complex evolution，SCE），以提高IBGOA特征选择算法的全局搜索性能。将改进后的算法称为混合二进制蝗虫优化算法（shuffled binary grasshopper optimization algorithm，SBGOA）特征选择方法。

2.3.1 混合复杂进化方法

混合复杂进化方法是由美国亚利桑那州大学的Duan 博士等[22]于1992 年提出的一种模拟自然进化过程的混合进化方法。该方法的原理是将全局搜索作为自然进化的过程，将群体公平地划分为几个子群，每个子群都被允许独立发展。在子群独立发展的过程中不断引入随机生成的新成员来替代最差个体。经过自定义次数的进化后，子群被迫重新混合，新的群体通过洗牌过程形成。这一策略有助于通过共享每个子群独立获得的信息和属性来改进算法。

SCE 划分子群独立进化、竞争淘汰的独特性质能够有效避免整个算法陷入局部最优，其在子群独立进化完成之后的强行混合可以使得大量搜索个体跳出其舒适圈，在更广阔的解空间内进行探索，从而使算法具有良好的全局搜索性能。

2.3.2 改进策略

SCE 优秀的全局搜索性能恰好可以弥补IBGOA特征选择算法全局搜索能力较差的缺陷，因此本文通过引入SCE 改进IBGOA 特征选择算法，改进的具体方法如下：

（1）排序与划分子群：在SBGOA 特征选择算法中，种群在每次进行更新之前需要根据每个个体的适应度对蝗虫群体进行升序排序。排序完成后根据群体中个体的顺序将整个种群划分为4 个子群S1、S2、S3、S4，每个子群含有M=N/4 个个体。为尽量减少每个子群中蝗虫群体优劣程度的差异，本文将X1划分到S1，X2划分到S2，X3划分到S3，X4划分到S4中，X5划分到S1中……，依此类推，直到XN划分到S4中后全部个体划分完成。

（2）子群更新：划分子群后独立地更新各子群，对于单个子群，每个个体基于该子群中其他个体的位置和该子群中最优个体的位置进行更新。为了保证算法的收敛能力，子群S1与S2按照基本方式进行更新；为了增强算法的全局搜索能力，子群S3与S4更新时的参数c=cmax，并且其不随迭代次数变化。

（3）子群复合：当所有子群经过自定义次数tsub次的更新后，将所有子群拆分并将全部个体混合成为一个新的群体。

综上可知，SBGOA 特征选择算法中的整个蝗虫种群被分为4 个子群，每个子群独立进化，并且强制混合。算法在探索阶段，各子群独立的风向（目标位置）可以避免蝗虫种群在同一方向进行探索，与IBGOA 比较，该策略有效提高了算法的探索能力；子群迭代完成后强制混合的策略可以提高蝗虫个体跳出原先舒适圈（舒适距离）的能力，强制个体改变搜索路径，提高了算法的跳出局部最优的能力。在算法后期的局部搜索阶段中，由于子群之间互不干扰，不同子群的个体间没有吸引或排斥力，增加了个体重合的概率，弱化了算法的局部搜索能力，而各子群独立的风向可以确保个体不会聚集收敛到同一个极值点，进一步降低了算法的陷入局部最优的可能，提高了算法的多样性和鲁棒性。

2.3.3 特征选择实现流程

SBGOA 特征选择算法的伪代码如下所示。

初始化SBGOA 特征选择算法参数cmax、cmin，最大迭代次数Tmax，子群迭代次数tsub

初始化数据集、数据集参数

按照2.1.1 小节的方法进行种群初始化，同时使用特征子集评价函数（见2.4 节）计算所有个体的适应度

时间复杂度分析：SBGOA 中个体更新仅需计算所在子群的其余个体位置，假设每个子群所含个体数量为M=N/4，则单个个体更新一次的时间复杂度为O(M)，子群更新一次的时间复杂度为O(M2)；假设单个子群更新次数为tsub，则整个种群更新一次的时间复杂度为假设最大迭代次数为Tmax，则可以得出SBGOA 特征选择算法的时间复杂度为由于子群迭代次数不会低于4（过低则无法正常收敛，没有意义），因此该算法的时间复杂度高于BGOA 与IBGOA 特征选择算法。值得一提的是，由于该算法采用分组更新且互不干扰的策略，可以并行实现，从而极大地缩短了算法的运行时间。

2.4 特征子集评价函数

为评价二进制蝗虫优化算法产生特征子集的优劣程度，本文基于K-NN 分类器与十折交叉验证法设计了一种特征子集评价函数（适应度函数）。该函数的基本流程为：将初始数据集分为10 份，其中9 份作为训练集，其余1 份作为测试集；利用二进制蝗虫优化算法中蝗虫个体的位置信息来截取特征子集；使用训练集训练K-NN 分类器并使用K-NN 分类器对测试集进行分类；采用十折交叉验证法进行10 次验证，得到该特征子集的分类错误率；将该特征子集的分类错误率与特征个数占总特征的比值按一定权重结合，按照式（13）计算该个体适应度fitness。

其中,ErrorRate表示该子集的分类错误率，FeatureNum表示该子集的特征个数，dim表示数据集的特征总数。本文算法意在保证低分类错误率的基础上降低特征数量，因此将分类错误率与特征数量的权重分别设置为0.99 与0.01。

由于特征子集为随机选择，那么可能会出现特征数量为0 的特征子集，但此时该特征子集无意义，因此需要对这种情况进行约束[23]。在特征子集评价函数中，本文将此类特征子集的适应度设置为1，以消除无意义子集对算法的不利影响。

3 仿真实验和结果分析

本文选择在机器学习领域中常用的UCI 数据集中的Breast Cancer、Soybean-large 等8 个数据集作为测试算法性能的数据集。选用的数据集与其属性如表2 所示。

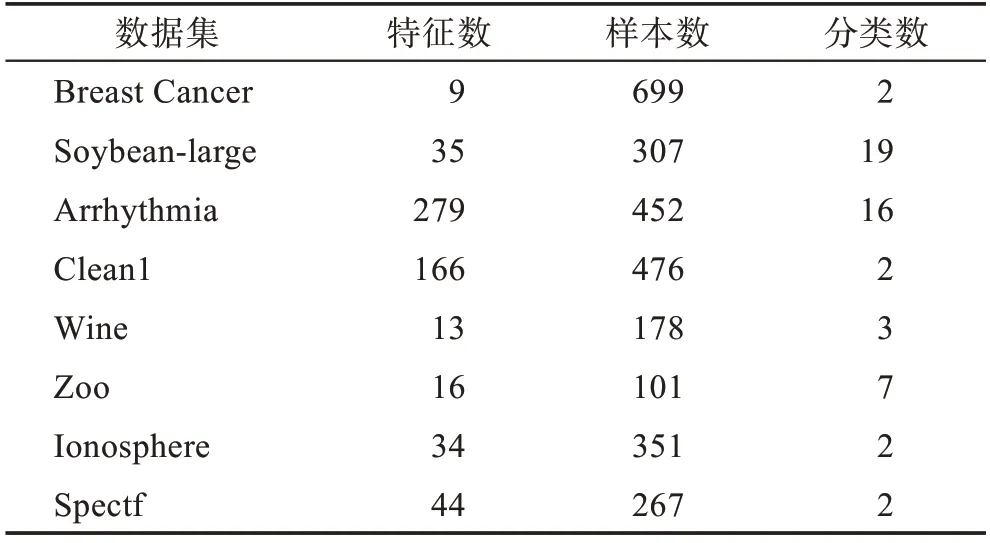
Table 2 Selected UCI data sets表2 选用的UCI数据集

3.1 实验参数设置

为了验证IBGOA 与SBGOA 的改进效果，并客观地评价SBGOA 的性能，本文使用BGOA 特征选择算法、IBGOA 特征选择算法、SBGOA 特征选择算法、二进制粒子群优化算法（binary particle swarm optimization，BPSO）[24]与二进制灰狼优化算法（binary grey wolf optimization，BGWO）[25]在表2 中的8 个数据集上进行对比实验。5 种算法的最大迭代次数均设置为20，种群大小均设置为80，其中SBGOA 特征选择算法的子群迭代次数设置为10。

3.2 实验结果分析

本文使用5 种算法分别对表2 中的数据集进行了10 次独立重复实验。实验中5 种算法均使用本文设计的适应度函数。实验结果如表3 所示，其中avg_fit与std_fit分别是10 次重复实验的平均适应度与标准偏差，Average 是8 个数据集平均适应度与标准偏差的平均指标。表中每个数据集对应的最低平均适应度已用粗体标出。

平均适应度表示10 次测试结果的适应度平均值，其值越低，则表示对应算法提高分类准确率和降维的性能越优。从表3 BGOA 特征选择算法与IBGOA特征选择算法平均适应度可以看出：对于Breast Cancer 数据集与Wine 数据集的测试结果，BGOA 特征选择算法的性能略优于IBGOA 特征选择算法，但对于其余数据集的测试结果来说，后者的性能明显优于前者。Breast Cancer 数据集与Wine 数据集的特征数量分别为9 与13，低与其他数据集，因此可以得出BGOA 特征选择算法在低维数据集的测试性能略优于IBGOA 特征选择算法，但对于高维数据集的处理性能来说，后者的表现更优。说明本文对BGOA特征选择算法的改进有效提升了算法在高维度下提高分类准确率与降低特征数量的性能。

从表3 SBGOA 特征选择算法、BGOA 特征选择算法、IBGOA 特征选择算法的平均适应度可以看出：对于8 个数据集，SBGOA 特征选择算法的平均适应度总是低于其余两种算法，表明SBGOA 特征选择算法提高分类准确率与降低特征数量的性能优于其余两种算法。说明本文对IBGOA 特征选择算法的改进有效提升了算法的全局搜索能力。

从表3 BPSO 特征选择算法、BGWO 特征选择算法与SBGOA 特征选择算法可以看出：对于8 个数据集，SBGOA 特征选择算法的平均适应度总是低于其他两种算法，说明SBGOA 特征选择算法在降低特征数量与提高分类准确率的性能优于其他两种算法。标准偏差反映了算法鲁棒性的优劣，即标准偏差的值越小，对应算法的鲁棒性越优。表4 为5 种算法对应8 个数据集的标准偏差排名与8 个数据集上的平均标准偏差，每个数据集对应的算法的标准偏差越小，则排名越靠前。

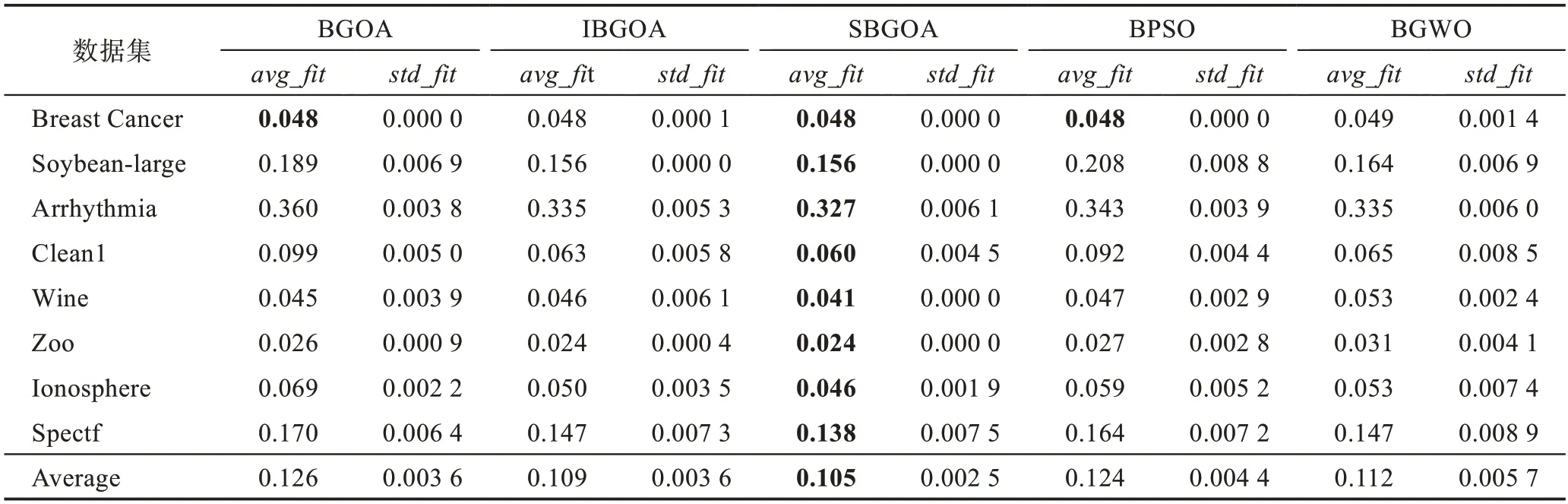
Table 3 Fitness and average index of 5 algorithms表3 5 种算法的适应度与平均指标

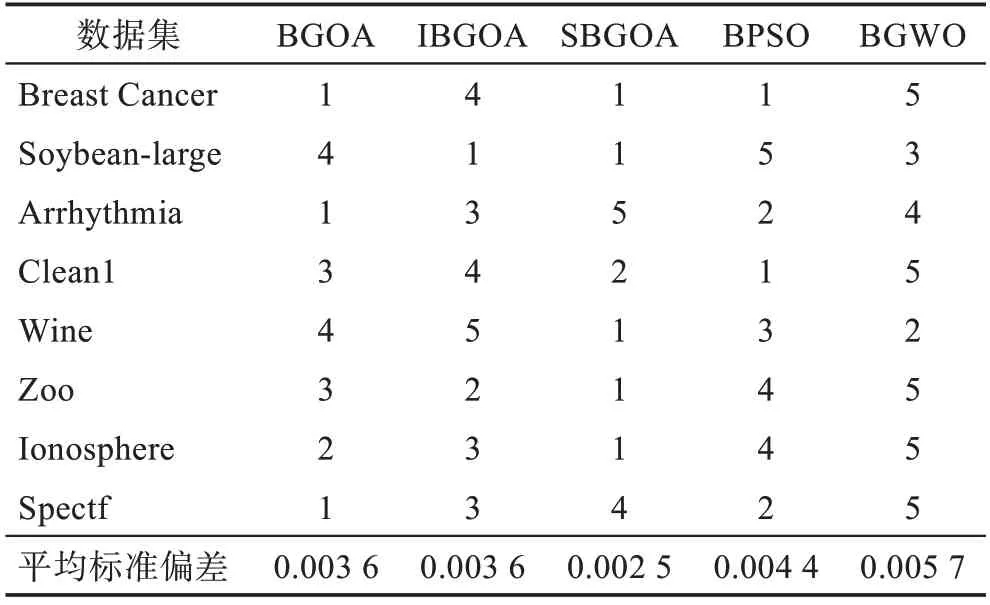
Table 4 Standard deviation ranking and average standard deviation of 5 algorithms表4 5 种算法的标准偏差排名与平均标准偏差

从表4 BGOA 特征选择算法与IBGOA 特征选择算法的排名情况可以看出：虽然两者在8 个数据集上的标准偏差排名参差不齐，但从平均标准偏差来看，两者标准偏差整体相差很小。表明两者的鲁棒性并无较大的差别。说明本文对BGOA 特征选择算法的改进并没有提升算法的鲁棒性。

从表4 SBGOA 特征选择算法与IBGOA 特征选择算法的排名情况可以看出：在Arrhythmia 与Spectf数据集上前者的标准偏差排名低于后者，但对于其他6 个数据集，前者的标准偏差排名均高于后者，并且前者的平均标准偏差明显低于后者，表明前者的鲁棒性优于后者。说明本文对IBGOA 特征选择算法的改进有效提升了算法的鲁棒性。

从表4 SBGOA 特征选择算法、BPSO 特征选择算法与BGWO 特征选择算法的排名情况可以看出：在Arrhythmia 数据集上，SBGOA 特征选择算法的排名低于其他两种算法；在Clean1 数据集上，SBGOA特征选择算法的标准偏差排名低于BPSO 特征选择算法，高于GWO 特征选择算法；在Spectf 数据集上，SBGOA 特征选择算法的标准偏差排名低于BPSO 特征选择算法，高于BGWO 特征选择算法；在其他5 个数据上，SBGOA 特征选择算法的标准偏差排名均高于其余两种算法，并且SBGOA 特征选择算法的平均标准偏差明显低于其余两种算法。表明SBGOA 特征选择算法的鲁棒性优于BPSO 特征选择算法与BGWO 特征选择算法。

本文使用上述5 种算法分别对8 个数据集进行了特征选择，并根据不同迭代次数下算法适应度值的变化趋势来评价算法的搜索性能与收敛性能。实验结果如图3 所示，其中X轴表示迭代次数t，Y轴表示最优适应度fitness。

图3（a）、（e）和（f）分别为5 种算法在Breast Cancer、Wine 和Zoo 数据集上的实验结果，从中可以看出：SBGOA 特征选择算法在上述3 个数据集上的收敛速度均快于其他4 种算法，并且搜索到的解优于其他4 种算法。图3（b）和（g）分别为5 种算法在Soybean-large 和Ionosphere 数据集上的实验结果，从中可以看出：SBGOA 特征选择算法在上述两个数据集上均于1 次迭代后便搜索到了适应度比其他4 种算法更低的解，并且始终能够在后续的迭代过程中搜索到比其他算法更优的解。图3（d）为5 种算法在Clean1 数据集上的实验结果，从中可以看出：SBGOA特征选择算法在前4 次迭代过程中均搜索到了比其他4 种算法更优的解，虽然在第5 至13 次迭代的过程中搜索到的解劣于BGWO 特征选择算法，但迭代14次以后搜索到了比其他4 种算法更优的解。图3（c）和（h）分别为5 种算法在Arrhythmia 和Spectf 数据集上的实验结果，从中可以看出：SBGOA 特征选择算法在上述两个数据集上分别迭代5 次、8 次时便搜索到明显优于其他4 种算法的解，并且在之后的迭代过程中仍然能搜索到适应度更低的解。综上可知，除去Clean1 数据集上第5 至13 次迭代的结果，SBGOA特征选择算法在各个数据集上每次迭代后搜索到的解均优于其他4 种算法。这表明相比于其他4 种算法，SBGOA 具有更优的搜索性能。SBGOA 特征选择算法在Breast Cancer、Wine、Zoo 3 个数据集上的收敛速度均快于其他4 种算法，通过表2 可知，Breast Cancer、Wine、Zoo 3 个数据集均为低维度数据集，这表明相比于其他4种算法，SBGOA特征选择算法在低维度数据集上具有更快的收敛速度。在Arrhythmia和Spectf 数据集上，SBGOA 特征选择算法不仅能在较少迭代次数的情况下搜索到明显优于其他4 种算法的解，而且后续的迭代过程中仍然能够继续搜索到适应度更低的解，表明SBGOA 特征选择算法的收敛性能优于其他两种算法。

综合来说，从提高分类准确率和降低特征数量方面、鲁棒性方面、搜索性能和收敛性能方面对比5种算法，SBGOA 特征选择算法的总体性能优于其他4 种算法。

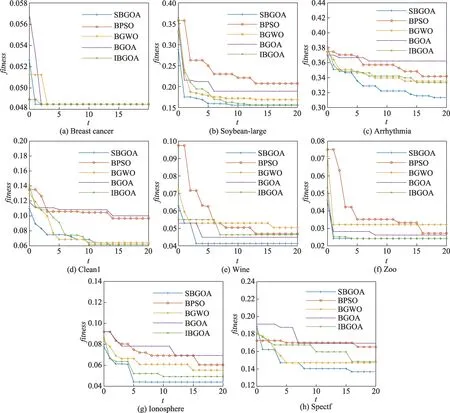
Fig.3 Line graphs of fitness of 5 algorithms with changing of the number of iterations图3 5 种算法适应度随迭代次数变化折线图

4 结束语

IBGOA 特征选择算法通过引入新的二进制转化策略，有效降低了特征选择算法二进制转换的盲目性；对IBGOA 特征选择算法引入混合复杂进化方法后提出的SBGOA，将蝗虫群体划分子群并独立进化，提高了算法的多样性，降低了早熟收敛的概率。仿真实验结果表明：IBGOA 特征选择算法有效提高了数据集的分类准确率，SBGOA 特征选择算法进一步提高了特征选择的全局搜索能力；与BGOA、IBGOA、BPSO 和BGWO 特征选择算法相比，SBGOA特征选择算法具有更好的性能。