基于局部密度离群点检测k-means算法*

刘 凤， 戴家佳， 胡 阳

(贵州大学 数学与统计学院，贵阳 550025)

0 引 言

聚类是无监督学习中一个重要的方法，它在一定意义上检测数据集中相似的对象，并形成群集的过程，这在大数据时代是很有必要的。聚类的最主要目的是使得群集与群集之间的距离最大化，群集内的对象距离最小化。同一个簇中的对象与该簇中其他的对象是非常相似的，不同群集之间中对象彼此差异是比较大的。MacQueen[1]提出k-means算法，该算法是一种最著名的划分聚类算法，其算法原理在聚类算法中是比较简单的，并且易于聚类。在实际生活中聚类分析也得到比较广泛的应用[2-4]。虽其原理简单，但是该算法也存在一些缺点，最主要有以下几个方面：对球状形数据集聚类结果较好，其他的数据集聚类结果相对较差；在聚类的时候容易局部收敛；k是随机的，需要在聚类的时候人为给定；聚类算法中初始聚类中心的选取问题；若数据集中有离群点、数据类型不一致等对聚类结果影响比较大。考虑这些不足之处，有大量学者对其不足进行改进，Arthur和Vassilvitskii[5]对其初始聚类中心随机性做改进，首先在数据集中随机选择一个数据点作为第一个初始聚类中心；其次在数据集中选择与第一个聚类中心相对最远的点作为第二个类簇中心，依据这种原理，直到选出k个群集质心。然而聚类中心的选择会影响聚类数目的准确性，Alibuhtto和Mahat[6]提出了一种基于距离的k-means算法，来确定聚类中的聚类数目。Masud等[7]提出了聚类数目与聚类中心的自动选择方法，Zhou等[8]提出了基于遗传算法的初始聚类中心的自动选择。大量学者也在算法中对k值进行了改进，Qi等[9]提出了层次k-means算法来确定聚类中的k值。程明畅等[10]提出了基于类簇之间分位数半径的动态k-means算法，改进的k-means聚类方法取得了良好的聚类效果。在聚类中，数据类型不一致以及离群点等会对聚类结果起到一定的影响，因此聚类中离群点的研究是近年来一个较为热门的课题。Zhang等[11]提出了一种加权距离测度的高斯函数优化k-means聚类算法。Jones等[12]提出了一种新的FilterK算法，通过降低离群值的影响来改善k-means聚类的结果，Yu等[13]将剔掉离群点检测，应用到隐私保护中，Neelima和Kumar[14]提出基于离群点检测应用到色调映射，数据集中有离群点对聚类的结果影响都比较大，基于离群点对数据集在聚类中影响比较大。

以上这些学者对k-means算法进行改进，使得k-means算法在聚类过程中k值的随机性得到一定的解决，并提供了类簇中心选择方法，但是对于数据集中的离群值对聚类过程产生较大的影响，笔者对数据集使用局部密度离群点LOF检测方法对数据集进行处理，将离群值从数据集中剔除之后再使用k-means算法聚类。

1 k-means算法与局部密度离群点检测方法

1.1 k-means算法

k-means算法是一种迭代算法，它是将数据集划分为k个预先定义的不重叠的群集。在这种情况下，每个数据点都属于一个群集。将数据集点分配到k个群集中，使数据点与群集的质心之间距离的平方之和达到最小。

k-means算法的5个主要步骤如下：

输入：数据集D={x1，x2，…，xn}，类簇数为k。

输出：k个类簇数C={C1，C2，…，Ck}。

Step1从数据集D中随机选择k个对象作为聚类中的初始中心。

Step2计算数据集D中的每一个对象到选取的k个对象之间的距离。

Step3根据Step 2将数据集D中的每一个对象划分到距离最近的类簇中，即满足下式：

dist(xi，Cj)=min{dist(xi，Cj)，i=1，2，…，n；j=1，2，…，k}

Step4重新更新每个群集的聚类中心，即

其中，Nj表示为第j个类簇中对象个数。

Step5反复进行Step 2、Step 3、Step 4，直到群集质心不再发生变化或者达到预先给定最大迭代次数，算法终止。

1.2 局部密度离群点检测法(Local Outlier Factor，LOF)[15]

先给出几个局部密度离群点检测LOF方法的相关定义：d(X，Y)表示对象X与对象Y的距离。对象X的第k_距离(k_distance)：对给定的正整数k，在样本空间Ω中，它与对象X之间的距离d(X，Ω)。样本空间Ω中最远的对象W与对象X的距离，不包括对象X，即k_distance(X)=d(X，W)。对象X的第k_距离邻域(Nk(X))：

Nk(X)={Y|d(X，Y)≤k_distance(X)}

可达距离(Reach Distance)：数据集中X与Y之间的可达距离为

reach_dist(X，Y)=max{k_distance(X)，dist(X，W)}

局部可达密度(Local Reach Density，LRD)：

局部密度离群值因子：

2 聚类有效性评价指标

评估聚类结果的好坏，聚类有效性指标应能提供一些关于数据集分类质量的评价。最重要的体现在“类簇间相似度比较低，类簇内相似度较高”。聚类有效性评价方法有很多，采用的聚类评价指标有：DB指标、Dunn指标和Silhouette指标。

2.1 Silhouette指标(fsilhouette)[16]

计算数据集中每一个数据点的轮廓系数如：

其中，db(i)表示为数据集中点i与其他各类簇中点距离平均值中的最小值，dw(i)表示为数据集中点i与该类簇中其他点距离的平均值。fsilhouette值在-1和1之间，若为1，则数据集中点i分配在相应的类簇是恰当的；若为-1，则数据集中点i应该分配在其他的类簇；若为0，则数据集中点i可以分配在该类簇中，也可以分配到其他类簇中。

2.2 Davies-Bouldin指标(fDB)[17]

数据集中fDB指标计算如下：

其中，σi，σj表示对应的类簇内距离的平均值，d(ci，cj)表示质心ci，cj之间的距离，指标值越小，聚类结果中类簇内部越紧密，类簇间越分离。

2.3 Dunn指标(fDunn)[18]

数据集中的Dunn指标如下：

其中,d(i，j)表示数据集中任意两个类簇之间的距离，d(k)表示数据集中任意类簇内距离。fDunn值越大，说明数据集的聚类结果较好。

3 实验结果及其分析

3.1 人工随机产生的数据集

人工生成的数据集，第一组为meanx1=3，meany1=2，方差为0.25的正太分布随机数；第二组为meanx2=3，meany2=8，方差为0.25的正太分布随机数；第三组为meanx3=9，meany3=5，方差0.25的正太分布随机数；第四组为meanx4=15，meany4=2，方差为0.25的正太分布随机数；第五组为meanx5=13，meany5=7，方差为0.25的正太分布随机数，每一组产生100个正太分布随机数；用runif函数生成均匀分布随机数，最小值为9，最大值为20。人工生成的数据集用来验证去除离群点之后的数据集与原始数据集做k-means聚类比较，其聚类图以及评价指标如图1—图3。

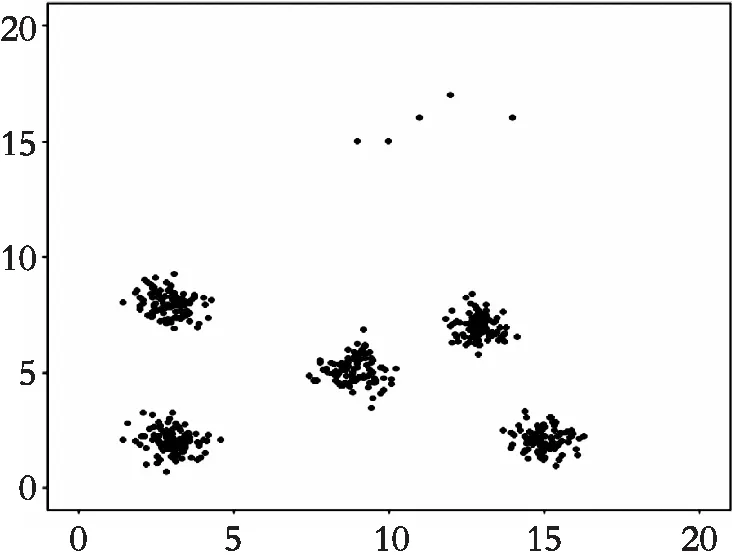
图1 原始数据集Fig. 1 The initial data set

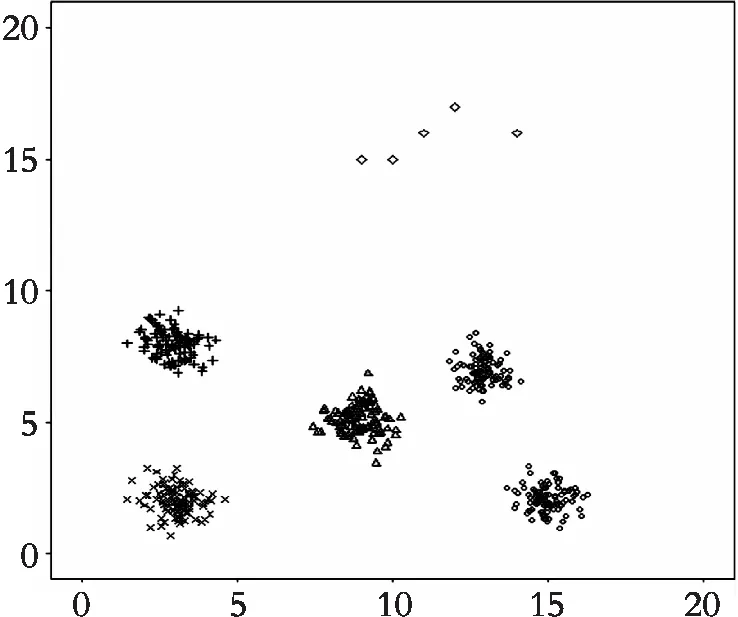
图2 原始数据集聚类图Fig. 2 The initial data set clustering diagram

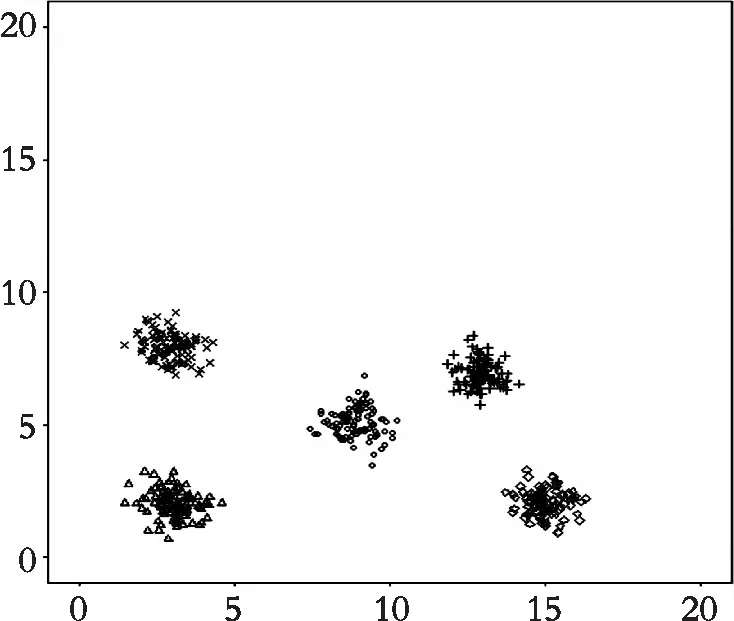
图3 去除离群值聚类图Fig. 3 The cluster diagram of removal of outliers

图2、图3具体体现由表1给出，表1给出了fDB指标、fDunn指标和fSilhouette指标。原始数据集k-means算法的fDB指标为0.442 5，去除离群值k-means算法的fDB值为0.281 5，去除离群值k-means算法的fDB值比原始数据集k-means算法的fDB值小，fDB值越小表明类簇内对象之间的距离越小，同时类簇间对象之间的距离越大，说明fDB指标的值越小越好，去除离群值k-means算法相比原始数据集k-means算法较好；fDunn指标和fSilhouette指标越大表明类簇对象之间的距离越大，且类簇内对象之间的距离越小，说明这两种指标的值越大越好，原始数据集k-means算法的fDuun值为0.414 1，fSilhouette值为0.718 8，去除离群值k-means算法的fDuun值为0.606 9，fSilhouette值为0.820 8，去除离群值k-means算法相比原始数据集k-means算法较好。表1证明了人工生成的数据集去除离群值在再用k-means得到的聚类结果比直接使用k-means聚类算法还要好。

表1 人工产生的数据集聚类评价指标Table 1 Evaluation index of manually generated data cluster

3.2 University of California Irvine(UCI)数据集

为了证明所提出的算法有效性，选了UCI数据集中的Wine和Seeds两个数据集来进行证明。表2给出了各个数据集的量，表3给出了Wine数据集使用k-means算法以及先使用局部密度离群点LOF检测方法剔掉离群点，再使用k-means聚类结果的3种聚类评价指标，表4为Seeds数据集使用k-means算法以及先使用局部密度离群点LOF检测方法剔掉离群点，再使用k-means聚类结果的三种聚类评价指标。

表2 数据集各个量Table 2 Each quantity of the data set

表3 Wine数据聚类结果的3种评价指标Table 3 Three evaluation indexes of Wine data clustering results

表4 Seeds数据聚类结果的3种评价指标Table 4 Three evaluation indicators for the clustering result of Seeds data

表3给出了Wine数据集的fDB指标、fDunn指标和fSilhouette指标。原始数据集k-means算法的fDB指标为1.468 1，去除离群值k-means算法的fDB值为1.196 8，去除离群值k-means算法的fDB值比原始数据集k-means算法的fDB值小，fDB值越小表明类簇内对象之间的距离越小，同时类簇间对象之间的距离越大，说明fDB指标的值越小越好，去除离群值k-means算法相比原始数据集k-means算法较好；fDunn指标和fSilhouette指标越大表明类簇对象之间的距离越大，且类簇内对象之间的距离越小，说明这两种指标的值越大越好，原始数据集k-means算法的fDunn值为0.232 3，fSilhouette值为0.284 9，去除离群值k-means算法的fDunn值为0.336 7，fSilhouette值为0.335 2，去除离群值k-means算法相比原始数据集k-means算法较好。；表4为Seeds数据集聚类结果的fDB指标、fDunn指标和fSilhouette指标。原始数据集k-means算法的fDB指标为0.884 3，去除离群值k-means算法的fDB值为0.702 0，去除离群值k-means算法的fDB值比原始数据集k-means算法的fDB值小，fDB值越小表明类簇内对象之间的距离越小，同时类簇间对象之间的距离越大，说明fDB指标的值越小越好，去除离群值k-means算法相比原始数据集k-means算法较好；fDunn指标和fSilhouette指标越大表明类簇对象之间的距离越大，且类簇内对象之间的距离越小，说明这两种指标的值越大越好，原始数据集k-means算法的fSilhouette值为0.471 9，去除离群值k-means算法的fSilhouette值为0.527 4，去除离群值k-means算法相比原始数据集k-means算法较好。在UCI数据集上验证了去除离群值再使用k-means算法得到的聚类结果都有明显的改善，得到的聚类较好。

4 局部密度离群值k-means算法在实际中的应用

新型冠状病毒疫情对经济以及人们的生活带来了极大的影响。选取中国部分省、市、自治区数据集(安徽省、北京市、福建省、广东省、广西壮族自治区、江西省、贵州省、河北省、海南省、河南省、吉林省、黑龙江省、湖南省、江苏省、辽宁省、内蒙古自治区、山东省、山西省、陕西省、四川省、天津市、云南省、浙江省、重庆市)，这24个省、市、自治区新型冠状病毒肺炎疫情数据，数据来源于各个省、市、自治区的卫生健康委员会官网，表5为2020年2月18日中国24个省、市、自治区新型冠状病毒肺炎的确诊人数。

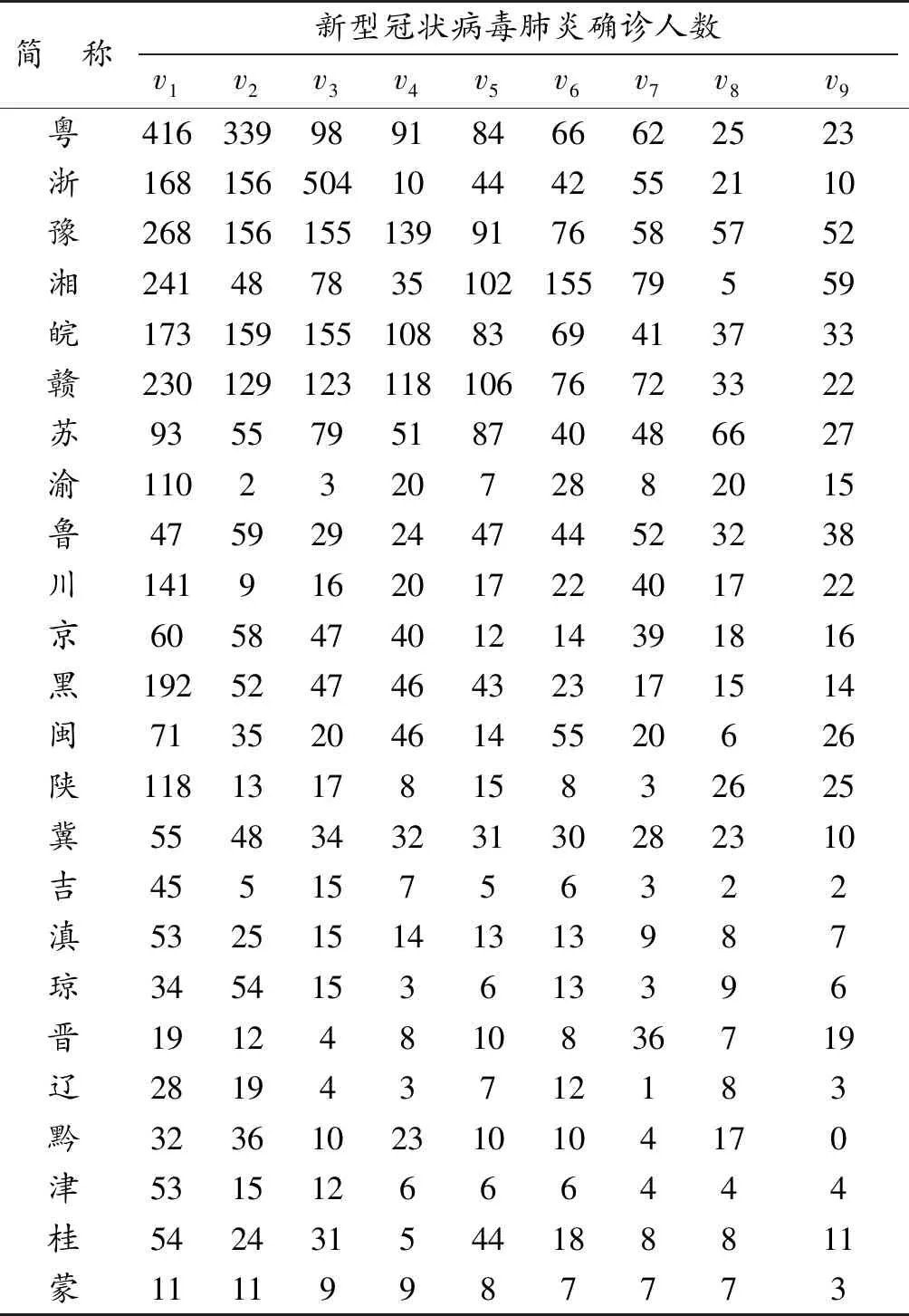
表5 2020年2月18日中国24个省、市、自治区新型冠状病毒肺炎确诊人数Table 5 The number of confirmed COVID-19 cases in 24 provinces， municipalities and autonomous regions in China on 18 February 2020

表5数据集比较大，先用scale对数据进行标准化再聚类，使用k-means聚类以及先使用局部密度离群值LOF检测方法去除离群值，再使用k-means聚类的3个评价指标如表6所示。

表6 24个省、市、自治区新型冠状病毒肺炎数据集聚类评价指标Table 6 COVID-19 data cluster evaluation indicators in 24 provinces, mumicipalities and autonomous regions

表6给出了24个省市以及自治区新型冠状病毒肺炎数据集聚类的fDB指标、fDunn指标和fSilhouette指标。原始数据集k-means算法的fDB指标为0.781 5，去除离群值k-means算法的fDB值为0.583 3，去除离群值k-means算法的fDB值比原始数据集k-means算法的fDB值小，fDB值越小表明类簇内对象之间的距离越小，同时类簇间对象之间的距离越大，说明fDB指标的值越小越好，去除离群值k-means算法相比原始数据集k-means算法较好；fDunn指标和fSilhouette指标越大表明类簇对象之间的距离越大，且类簇内对象之间的距离越小，说明这两种指标的值越大越好，原始数据集k-means算法的fDunn值为0.432 1，fSilhouette值为0.553 7，去除离群值k-means算法的fDunn值为0.665 2，fSilhouette值为0.581 4，去除离群值k-means算法相比原始数据集k-means算法较好。证明了使用局部密度离群值检测LOF方法对数据集剔除离群值之后再使用k-means算法得到的聚类结果较好，并且使用局部密度离群值检测LOF方法能更好地帮助分析每个地区的新型冠状病毒肺炎疫情情况，能让每个地区政府更好地处理医用物资的调配以及疫情防疫问题，更好降低经济的损失。

5 结束语

基于局部密度离群点检测k-means算法中，通过fDB指标、fDunn指标和fSilhouette3种评价指标进行聚类结果评价：

(1) 在人工产生的数据集中，通过3种评价指标得到去除离群值之后得到的聚类结果较好。

(2) 在UCI数据集中的Wine与Seeds数据集进行验证，使用本文选用的3种评价指标进行评价，得到的聚类结果较好。

(3) 将离群值检测k-means算法应用到新型冠状病毒肺炎疫情数据分析中，得到较好的聚类结果，更好帮助决策者做决策。

(4) 未来将对任意数据集的聚类以及聚类的类簇中心的选择进行研究。