养老保险及医疗保险水平对生育水平的影响分析

徐康顺 范君晖

随着生育成本的提高和生育观念的转变，我国人口生育的形势已经出现了重大转折，2019年出生人口已经降至近50年来的最低值[1]，同时，低生育水平下人口结构的长期失衡，使得老龄化和少子化叠加出现，人口的长期健康发展面临严峻挑战。面对生育形势出现的深刻转变，生育政策进行了大幅度改革，但就目前政策实施的结果来看，低生育水平的趋势并未得到有效扭转，这可能说明生育政策限制已不是现阶段低生育水平的主要原因。人口经济学家哈威·莱宾斯基于“成本-效益”分析提出的边际孩子数量选择理论[2]，为生育研究提供了视角，即生育决策者是否生育子女，生育几个子女主要取决于生育需要的成本和所能带来的潜在效益之间的比值。以此，众多学者[3-4]从经济成本、时间成本、机会成本、保险功能等角度进行了生育水平的影响因素分析。社会保险作为养老的重要补充手段，其对生育的保险功能可能产生的影响是学界研究的热点，但目前研究集中于养老保险与生育水平的关系，忽略了医疗保险同样可能对养儿防老的生育观念产生替代作用，进而对生育产生影响。同时，现有研究多从静态角度分析，忽略了影响可能具有长期性。因此，我们从动态角度分析养老及医疗保险水平对生育水平的影响，以期为政策改革提供参考。

1 指标选取及数据来源

1.1 指标选取

目前关于养老保险水平和医疗保险水平学界没有形成统一的评价指标。穆怀中[5]是国内最早对社会保障水平概念进行界定的学者，他以社会保障支出总额与国内生产总值的比值来衡量社会保障制度的发展与社会经济的发展的匹配程度，以此评价社会保障水平的高低，本研究借鉴其方法将养老保险、医疗保险水平界定为养老保险基金、医疗保险基金的支出额同财政总支出的比例。其中生育水平包括：生育率、总和生育率等。生育率会受到人口基数的影响，在人口基数小的时候，出生人口的增加会因为公式计算分母较小而出现出生率的快速上涨，易造成偏差。总和生育率通过计算15 ～ 49岁育龄妇女的分年龄组生育率的总和[6]得出，用来衡量妇女在育龄期平均生育子女的数量，其数据更加直观，且受人口结构变化的影响较小，常用来反映生育水平的变化趋势，因此，我们以总和生育率作为生育水平的代理指标。

1.2 数据来源

养老保险基金支出来自于国家统计局，鉴于新型农村养老保险全面推行的时间为2009年[5]，国家统计局的新型农村养老保险仅有2009和2010年这2年的数据，而2011年后的新型农村养老保险数据与城镇居民养老保险[7-8]数据合并为城乡居民养老保险进行统计，因此，每年的养老保险基金支出计算方式有所不同，具体为：2000—2008年为城镇职工养老保险基金支出数据，2009—2010年为城镇职工养老保险基金支出与新型农村养老保险基金支出的和，2011—2019年则为城镇职工养老保险基金支出与城乡居民养老保险基金支出的和；医疗保险基金数据来源为国家统计局，医疗保险同养老保险相似，都经历过农村居民和城镇居民保险合并的过程[9-10]，但国家统计局医疗保险的相关数据并未将城乡医疗保险数据与城镇职工医疗保险数据分开统计，因此，医疗保险基金支出的统计数字可以直接从国家统计局网站获取，数据选取范围为2000—2019年；财政支出总额数据来源于国家统计局年度数据中的财政类别，数据选取范围为2000—2019年；生育水平以总和生育率来衡量，总和生育率宏观数据无全国范围内的统计，仅能在第6次人口普查等少数调查数据中获得，因此，总和生育率数据多为抽样调查数据间接计算得出，姜全保等[11]通过4种不同的测量方法对总和生育率进行计算，其方法缺失值少，可靠程度高，因此，我们使用其预测模拟法获得的2000—2018年总和生育率数据，并根据同样的方法计算出2019年的总和生育率数据，以此作为生育水平的时间序列数据。

2 结果

2.1 基本情况

根据界定，2000—2019年养老保险水平(endowment security level, ESL)、医疗保险水平(medical security level, MSL)与生育水平(total fertility rate,TFR)的数据计算汇总于表1。

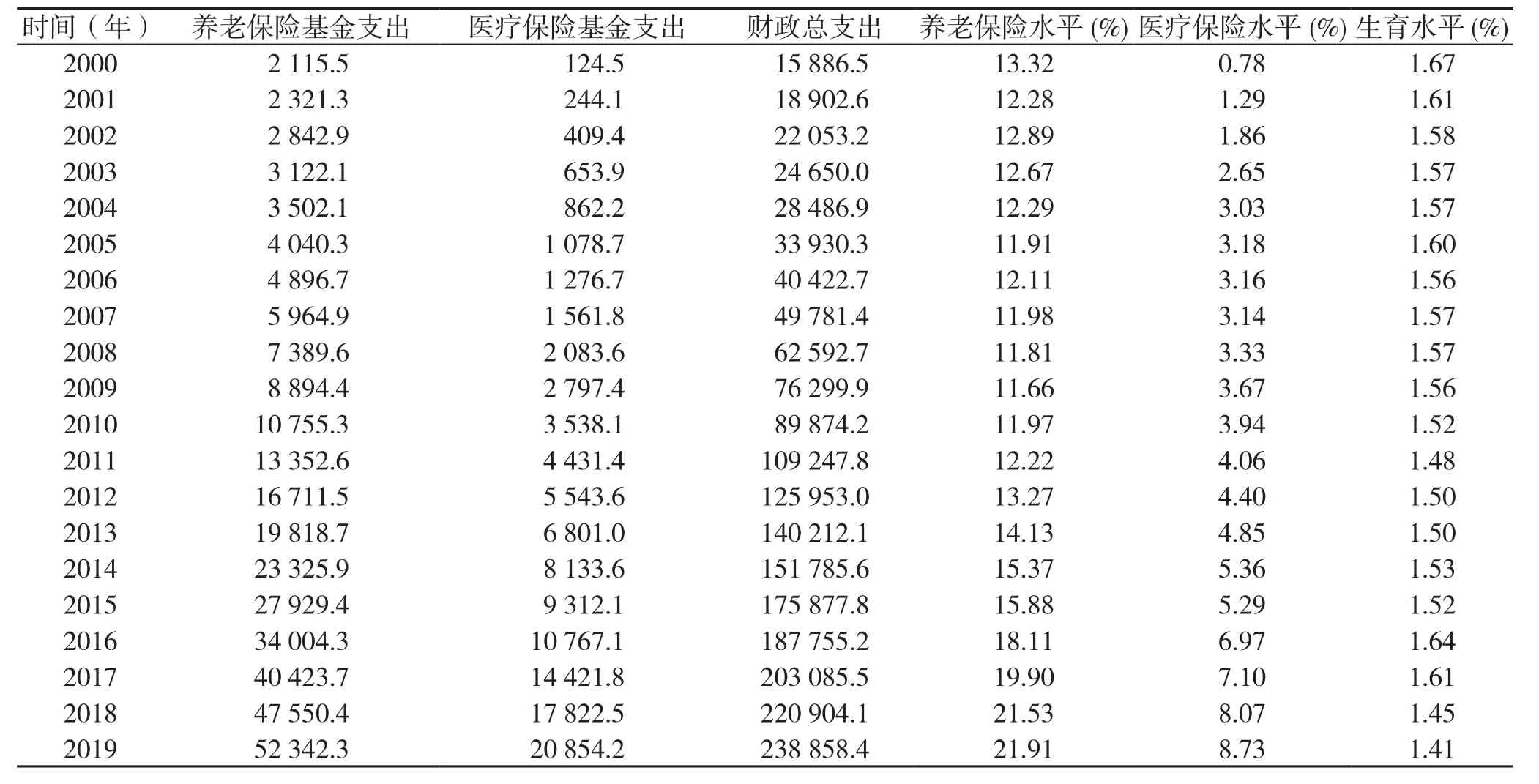
表1 养老保险水平、医疗保险水平、生育水平统计

2.2 模型选择与单位根检验

2.2.1 模型选择

VAR模型（向量自回归）最初由2011年诺贝尔经济学奖获得者Sims Christopher于1980年提出，该模型以多个回归方程式组合的形式出现，通过做自变量的若干滞后期数值来分析其因变量的回归关系，进而估计出全部研究变量之间的动态关系，常用来衡量社会经济指标之间的动态线性关系，公式为：一个N维P阶（维数代表研究变量的个数，阶数代表变量的滞后期数）的VAR模型的标准形式如下：

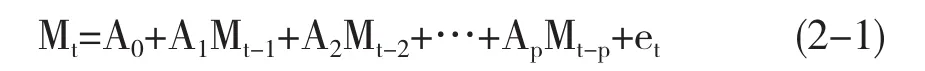
其中A0是截距项，Ai为回归系数，p是滞后阶数，et是随机误差项。

VAR模型通常使用矩阵的形式表示：

从2-2式中可以看出，Mt表示研究内生变量的列向量，可以理解为因变量的列向量。VAR模型的内生变量因不需要严格的理论条件，通过对自变量做滞后阶数的回归分析，既可以研究不同内生变量对因变量的滞后期影响，也可以研究内生变量自身对自身是否存在滞后效应，同时因只研究内生变量的滞后项，就避免了模型中出现同期变量，避免自相关性的出现。模型的估计采用最小二乘法，方差的平方和为最小，拟合效果更好。养老保险水平、医疗保险水平同生育水平是典型的动态时间序列数据，VAR模型通过变量滞后期的回归分析易于研究变量之间的动态关系。

2.2.2 单位根检验

在进行VAR模型建模之前，需要对变量进行单位根检验，以避免时间序列数据出现虚假趋势而造成伪回归。单位根检验又以ADF检验为最常用，使用EVIWES软件进行ADF单位根检验，结果见表2。

由表2可知，ESL、MSL、TFR这3项的ADF统计量均>1%、5%、10%下的临界值，即表示ADF检验不能拒绝原假设，说明变量序列不满足平稳性要求。检验结果不能拒绝原假设的情况下，需要对其一阶差分序列进行单位根检验，结果见表3。

表2 ADF统计

由表3可知，一阶差分后的DESL、DMSL、DTFR其ADF统计量分别小于10%、1%和5%的临界值，均小于10%的临界值，即表示变量序列均拒绝原假设，皆满足平稳性要求。

表3 一阶差分ADF检验统计

2.3 VAR建模分析

在定义VAR模型之前，一个关键的因素是需要对其进行滞后阶数的确定。滞后阶数的选择在VAR模型中非常重要，当选择的滞后阶数高于真实的滞后阶数时，模型出现过度拟合的状态，使得VAR模型的均方预测误差增大。然而，当选择的滞后阶数过小时，又会导致VAR模型的误差项出现自相关情况。因此，需要对VAR模型的滞后阶数进行准确的检验，目前常用的滞后阶数检验方法主要有似然比检验(LR)、赤地信息准则检验(AIC)、施瓦茨准则检验(SC)和汉南-奎因准则检验(HQ)。使用EVIEWS软件进行滞后阶数检验，结果见表4。

表4 滞后阶数检验

根据表4结果可知，LR检验值最大值在滞后1期，AIC、HQ检验值的最小值在滞后2期，SC检验值最小值在滞后1期，在AIC检验值和SC检验值不在同一列的情况下，以AIC检验值作为选择，因此，选择滞后2期作为建立VAR模型的最优滞后阶数。在完成平稳性检验和最优滞后阶数选择后，根据公式2-1，将一阶差分后的DESL、MSL、DTFR作为内生变量，常数项C作为外生变量，使用Eviews软件进行滞后二阶的模型计算，可得以下回归方程：

从生育水平的VAR公式2-3来看，医疗保险水平的滞后期对生育水平有非常明显的负向挤出效应，滞后1期和滞后2期的影响系数达到了-4.1和-4.19，医疗保险水平每提升1%，生育水平就下降4%以上。养老保险的滞后期对总和生育的影响，第1期为-1.91，第2期为2.7，养老保险水平对生育水平的影响具有先负后正的滞后效应。从影响系数来看，养老保险水平的提升，滞后1期内可能显著降低生育水平，即养老保险水平每提升1%，生育水平随之下降1.91%，但滞后2期影响关系将显著转正，养老保险水平每提升1%，将对生育水平有2.7%的促进作用。

2.4 脉冲响应与方差分解

2.4.1 脉冲响应

VAR模型通过构建自变量的滞后期函数来研究变量之间的动态关系，但其无法衡量变量之间的当期关系，而脉冲响应分析通过做误差项的冲击反应，同时根据期数的不同，可以做变量之间的中长期影响关系分析，因此，脉冲响应分析通常作为VAR模型的补充部分出现在建模分析的过程中，下文使用EVIEWS进行脉冲响应分析，横轴是观察期的期数，观察期设置为20期，纵轴是单位冲击所引起响应变量波动的值，曲线展示的是脉冲响应函数。

由图1可知，养老保险水平给予生育水平1个单位的正向冲击，生育水平会在当期做出正向反应，系数为0.027，并在第2期快速由正转负，第4期时再次转正，基本以2期为单位上下波动，在14期之后逐渐收敛，实际上，收敛仅仅是系数趋近于0，但并未实际达到0，养老保险水平对生育水平的影响，在15 ～ 20期内同样存在，但在2 ～ 4期的变化趋势中与VAR模型分析相似，即养老保险水平对生育水平有一定的负向影响，因此，脉冲响应在第2期（VAR模型的滞后1期）及之后的影响关系更加可靠，可见养老保险水平对生育水平的影响总体也是先负后正，并不是保持稳定的正向或负向关系。

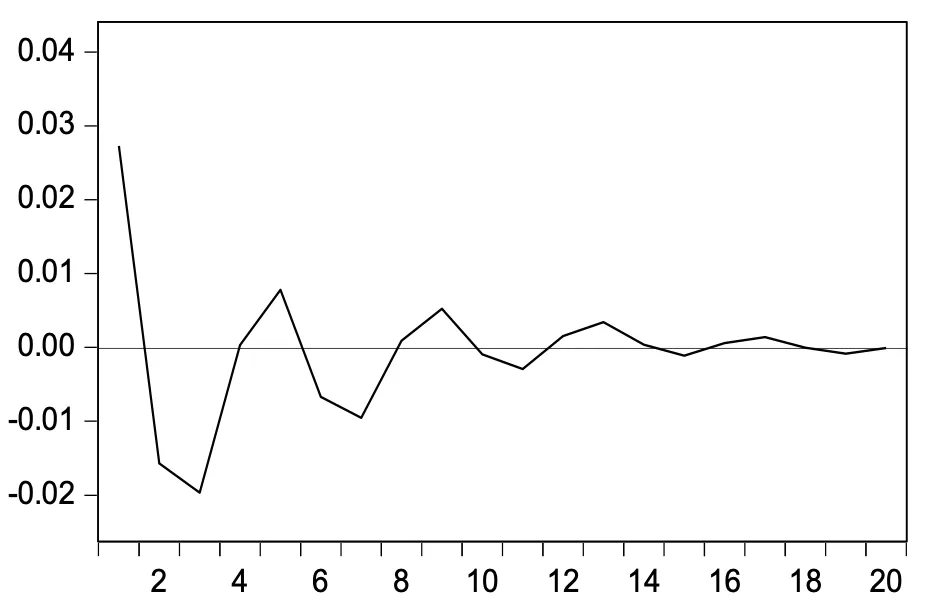
图1 养老保险水平对生育水平的脉冲响应

由图2可知，医疗保险水平给予生育水平1个单位的正向冲击，生育水平在当期会做出正向反应，随后在第2期会快速转负，在第4期再次转正，且在第14期后趋于收敛（同养老保险相似，医疗保险水平对生育水平的影响在15 ～ 20期内同样存在，但影响系数十分微弱）。医疗保险水平对生育水平的影响同养老保险水平对生育水平的影响有高度的相似性，基本都以2期为单位上下波动，且考虑生育行为的时间滞后性，都在第2期为负，随着时间的推移影响会逐渐转正。

图2 医疗保险水平对生育水平的脉冲响应

2.4.2 方差分解

方差分解是通过分析脉冲响应对模型各个结构冲击产生的影响，进而衡量自变量对因变量的动态贡献程度的一种方法，可理解为自变量随着时间的推移对因变量变化趋势的重要性，通常作为VAR模型建模的补充分析部分，使用Eviews软件进行方差分解，分别以养老保险水平、医疗保险水平及生育水平作为自变量，研究其对因变量的贡献程度。图3中，横轴代表观察期期数，以20期为观察周期，纵轴代表的是自变量对因变量的贡献率(%)，曲线代表自变量对因变量贡献程度的时间变化函数，其中DESL代表养老保险水平对生育水平贡献程度的时间变化函数，DMSL代表医疗保险水平对生育水平贡献程度的时间变化函数，DTFR代表生育水平对自身贡献程度的时间变化函数。

由图3可知，生育水平的贡献程度中，其自身的贡献程度最大，在第1期达到了64.8%，随后小幅度下降，在第3期下降到56.3%后趋于稳定，可以看出，生育水平对自身的波动影响十分明显，即生育水平的变化，有超过一半的贡献来自于其自身；养老保险水平、医疗保险水平对生育水平的贡献程度曲线具有相似性，都在第1期最低，分别为24.9%、10.3%，随后均小幅度上升，分别在第2期和第4期达到最大值28.7%和16.9%，随后趋于稳定。养老保险水平、医疗保险水平对生育水平的影响在前期呈现上升趋势，随后趋于稳定，说明养老保险水平和医疗保险水平对生育水平的影响具有一定的滞后性。

图3 养老保险水平、医疗保险水平、生育水平对生育水平的贡献程度

3 讨论

根据实证分析，养老保险水平对生育水平滞后1期时具有抑制作用，滞后2期时，养老保险水平对生育水平的影响由-1.91转为2.7。脉冲响应结果与VAR模型的结论基本相似，即脉冲响应2期（VAR滞后1期）时，养老保险水平会对生育水平产生负向的挤出效应，第3期时，会由负向挤出效应转变为正向的收入效应。方差分解中，养老保险水平的变动对生育水平变动的解释程度在第2期可达到28%，并且其他期数的系数也较为稳定，说明养老保险水平对生育水平的变化有一定的重要性。综合分析认为，养老保险水平对生育水平的影响机制前期为负，随着时间的推移逐渐转正，且影响可能达到15年以上。目前国内外养老保险与生育水平的研究中，主流观点认为养老保险水平的提高对生育水平的保险功能产生替代效应，进而抑制生育水平的提升[12-14]，也有部分学者[15-16]发现，在考虑收入的前提下，养老保险水平的提升有助于降低生育成本，进而对生育意愿和生育数量起到促进作用，而本研究结论与上述文献存在一定出入，认为养老保险水平对生育水平的影响具有动态变化，且与Gary等[17]在非利他性假设下的研究结论相似，即养老保险对生育水平的负面影响会因制度的完善而逐渐消失甚至转正。因此，推进养老保险制度完善可能有助于养老保险对生育水平产生正向促进作用。

医疗保险水平在滞后2期内均为负影响，且影响的绝对值较大，分别为-4.1和-4.19。脉冲响应发现医疗保险水平对生育水平的影响也存在由负转正的情况。而方差分解中，医疗保险水平对生育水平的最大解释程度仅为16%。因此，就医疗保险水平对生育水平影响的VAR模型系数、脉冲响应系数、方差分解系数综合来看，VAR模型系数的绝对值较大，而脉冲响应和方差分解系数的绝对值较小，这可能说明医疗保险水平对生育水平的影响主要体现在VAR模型的滞后2期内，以短期负向影响为主。目前关于医疗保险对生育水平影响的相关研究十分有限，且研究观点大相径庭，以医疗保险对生育水平无显著影响[18]、医疗保险对生育水平具有负向影响[19]和根据保险类型的不同影响具有异质性[20-21]3种观点为主。我们的分析结论与部分文献相似，虽然研究结论认为医疗保险水平对生育水平的影响以短期负向为主，但提高医疗保险水平对降低家庭医疗负担依然具有重要现实意义，并可能对降低生育成本、提高生育水平具有潜在影响。

本研究针对养老保险及医疗保险水平对生育水平的影响，从滞后期动态视角对三者进行了分析，弥补了相关文献研究在动态分析上的欠缺，同时研究结论为制定养老保险与生育水平协调发展的政策提供了实证参考，并且弥补了医疗保险对生育水平实证研究的空白，提供了新的实证研究证据。通过宏观经济的分析，有利于把握社会经济指标之间的整体关系。但生育行为十分复杂，尤其受个人层面，如经济、教育、性别等因素的影响，而宏观经济分析无法准确衡量个体在宏观政策对生育意愿产生影响的过程中可能做出的不同政策反应，进而可能造成政策评估的失真，这也是本研究的主要不足之处。因此，从微观层面将个人、经济、政策因素等指标与养老保险、医疗保险保障水平的变化进行结合，进一步分析养老保险与医疗保险对生育水平的影响是否会因为微观指标的影响而产生不同，对于进一步提高研究的政策参考可靠性十分必要，也将是本研究后续的研究重点。