一道高考函数题的一题多解及思考

周 振 (安徽省蒙城县第一中学 233504)

1 真题分析与解答

(2017年新课标全国I卷)已知函数f(x)=ae2x+(a-2)ex-x．

(1)讨论f(x)的单调性；

(2)若有两个零点，求a的取值范围．

1.1 题目分析

本题是典型的函数题，函数部分是贯穿整个中学时代的重要知识点．函数知识具有非常强的抽象性，难度系数也是千变万化，有时只要稍微变动其中的常数，就能使难度系数顿时“过山车”．同时也正因函数知识的多变性，相应题目既可以是简单的选择题，也可以是高考数学的压轴题．

上述题目以压轴题的设计来考查学生的数学综合素养，题目的主干非常简练，很容易使学生产生本题非常简单的错觉，甚至会有眼高手低的态度，但实则不然．参数在函数表达式中的存在直接将这道题目的难度系数拉升到了一个新的高度，虽然函数单调性的判断并不算困难，但是在第(2)题中关于参数的取值范围讨论，学生需要经过严谨的题目分析和大量的计算才能得到正确的范围．

关于第(1)问函数单调性的解答，我们可以结合函数与导数部分的相关知识，先求f(x)的导函数，然后令导函数等于0并得到关于未知数x的具体函数值，那么函数的单调性就一目了然．第(2)题的解答过程相对复杂一些，函数的零点不仅与导函数有着密切关系，参数值的具体变化也会影响整个函数的零点分布．而且经过第(1)题的铺垫性计算，整个函数的增减性是已知的，所以这一结论在第(2)题中也要被有效利用起来．

1.2 解题方法研究

对题目进行初步的分析后，有了明确的解答思路．具体的解答步骤可以参考以下三种.

方法1 (1)由于f(x)=ae2x+(a-2)ex-x，所以f′(x)=2ae2x+(a-2)ex-1．

当a=0时，f′(x)=-2ex-1<0，所以f(x)在定义域R上为减函数．

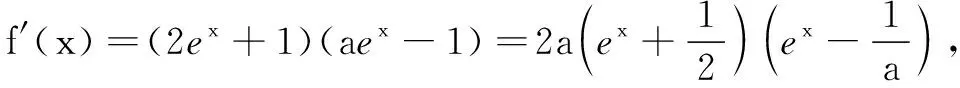
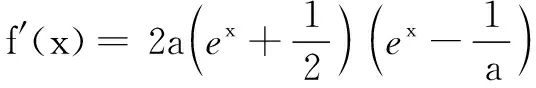
(2)根据上述计算结果，可以得知：

当a≤0时，f(x)在R上单调递减，所以此时的函数图象与x轴最多只有一个交点，与题目要求相矛盾，故a≤0不成立．

方法2 (1)同方法1．

(2)①若a≤0时，由(1)可知f(x)最多只有一个零点．

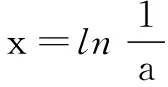
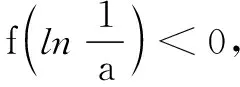
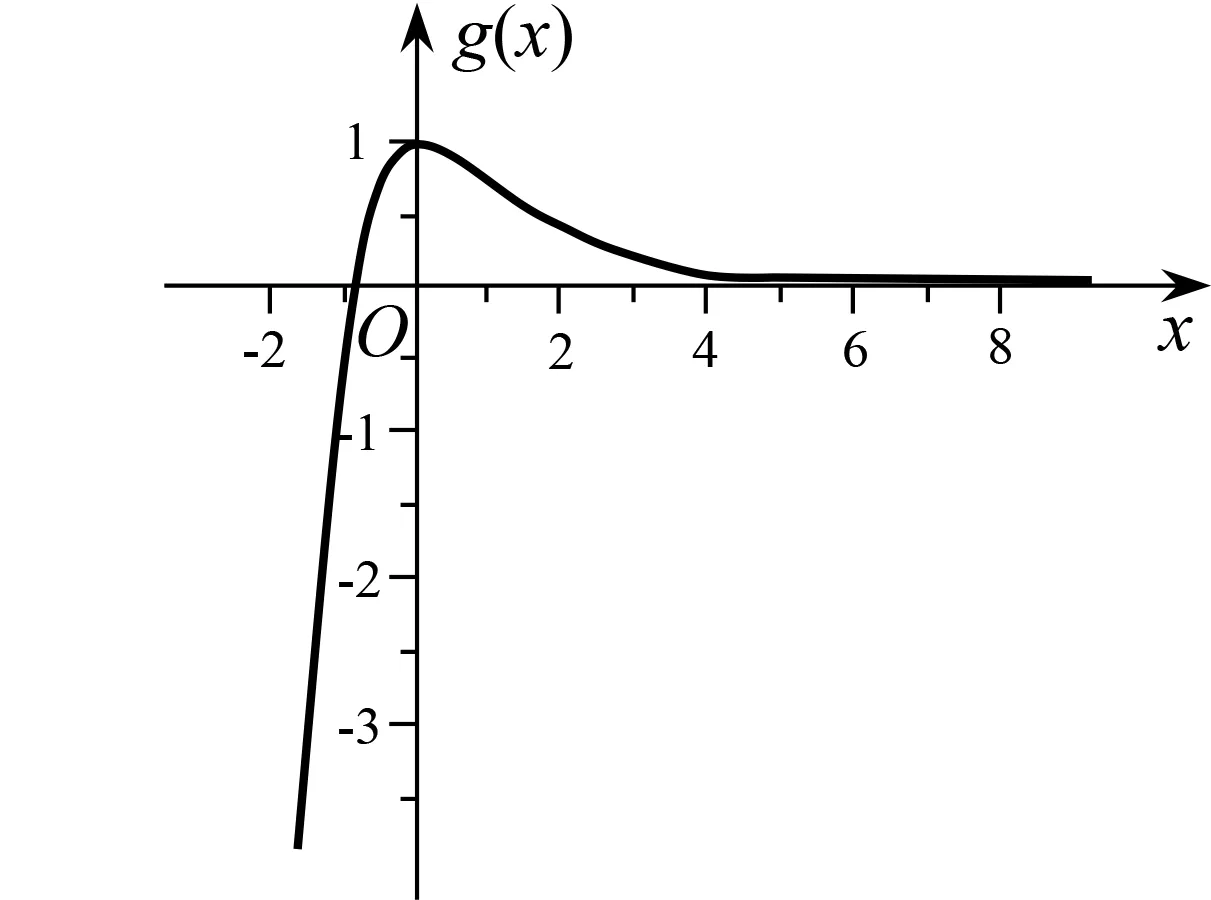
图1

若f(x)有两个零点，则说明y=a与y=g(x)有两个交点，由图1得a的取值范围是(0,1)．

2 一题多解的研究思考

2.1 优化读题和解题二者的顺序

对于上述题目的分析与解答，不仅让我们准确定位题目的考查重点，更重要的是通过这道题目可以折射出教师对数学教学工作的思考和启示．

教师要将侧重点放在读题和解题的顺序上，引导学生不断优化个人的读题和解题顺序．很多学生拿到题目便立即动手计算，这不是好的习惯．看到题目之后，首先要把题目仔细阅读一遍，并针对题干的条件进行详细的分析和解读，准确认识题干给出的每个条件所反馈的基本信息以及知识点内在的联系．例如，第(2)题给出的已知条件是函数f(x)有两个零点，说明函数图象和x轴有两个交点，这是题中隐含的已知条件．教师要培养学生先读题、后分析的好习惯，在每次测验或课后练习中，建议学生花一至两分钟的时间阅读题目并分析已知条件，当学生适应这种学习习惯后，那么对其数学能力的提升将有事半功倍的效果．

2.2 教学要秉持灵活性原则

虽然高中数学试题的答案是唯一的，但许多题目的解题方法却是多样的．数学教师在开展日常教学活动的过程中，要秉持灵活教学的基本原则，尤其对于重点和难点题型要积极引导学生尝试应用多种方法、探索多种解决问题的思路．一题多解不仅可以帮助学生系统化地梳理课本上的数学知识，更有助于学生养成灵活的解题方式.当一种解题思路受阻时，可以调整思路另寻他法，而不是钻牛角尖或者一条道走到黑．这不仅能够使学生顺利通过“考关”，也是STEAM类型的人才培养关键所在，并有效地促进素质教育的理念在一线教学中扎根发芽．

例题的第二种解法更偏向于证明法，由已知条件函数在区间上存在零点，紧紧围绕这一命题进行分析与论证，同时解答过程中，注重融合反证法，培养学生利用逆向思维解决问题的能力．假设不存在点m，当得出结论与题目已知条件相矛盾时，就能得到相反的结论．教师在数学教学过程中要重视对学生发散性思维的培养，通过灵活的教学方法，积极引导和鼓励学生多思考、多讨论、多交流，进而提升学生的数学综合素养．

3 结语

不管未来高考如何改革，教育教学评价体系如何变化，数学终究是支撑物理、化学等现代科学技术发展的一门重要的基础学科．在解决数学问题、不断探索解题路径时，不仅可促进学生对数学知识体系的巩固与提高，更能对高中物理、化学等知识的理解与掌握起到很大的助推作用．随着信息技术学科在高中学段逐渐获得重视，学生的编程等计算机水平逐步提升，适时将GeoGebra等软件融入课堂，能使抽象、复杂的函数问题可视化和动态化，这不仅促进学生对函数知识的理解，也为一题多解提供新路径．作为一线教师，唯有树立终身学习的理念，才能将授道解惑诠释好，才能更好地引导学生多渠道、全方位地探索一题多解的路径．