解题运算要提升 结构分析应先行

宋予林 (江苏省灌南高级中学 222599)

张奠宙先生认为数学核心素养包括真善美三个维度[1].具体地说，所谓“真”，即理解数学文明的文化价值，体会数学真理的严谨性、精确性；所谓“善”，指的是用数学的思想方法分析和解决实际问题的基本能力；所谓“美”，则是说能够欣赏数学智慧之美，喜欢数学，热爱数学．但是，笔者通过高三一轮的复习教学发现，学生在学习数学的过程中无法去真正体会数学的“真善美”，无法运用数学的“真善美”去分析解决数学问题，提升数学素养．笔者尝试结合最近在高三一轮复习中出现的一些问题与解决策略，谈谈如何通过观察与分析数学式子的结构，提升高三学生的运算素养．

1 感知数式的代数结构，培养学生运算观察能力

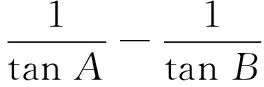
点评通过对数式的观察，结合直观想象，把待求式化归到①式的结构上，显然大大减少了解题运算的繁锁程度．因此，在高三一轮复习过程中，需要提高学生的解题运算能力，首先就要引导学生学会用数学的眼光观察世界．

2 观察数式的几何结构，培养学生运算转化能力

华罗庚先生曾说道：“数与形，本是相倚依，焉能分作两边飞．数缺形时少直观，形少数时难入微．”因此，对于例1的解法，笔者又在课堂中不断地去引导学生继续观察数式的几何结构，培养学生的运算转化能力．以下再给出两种不同的数形结合的思路．

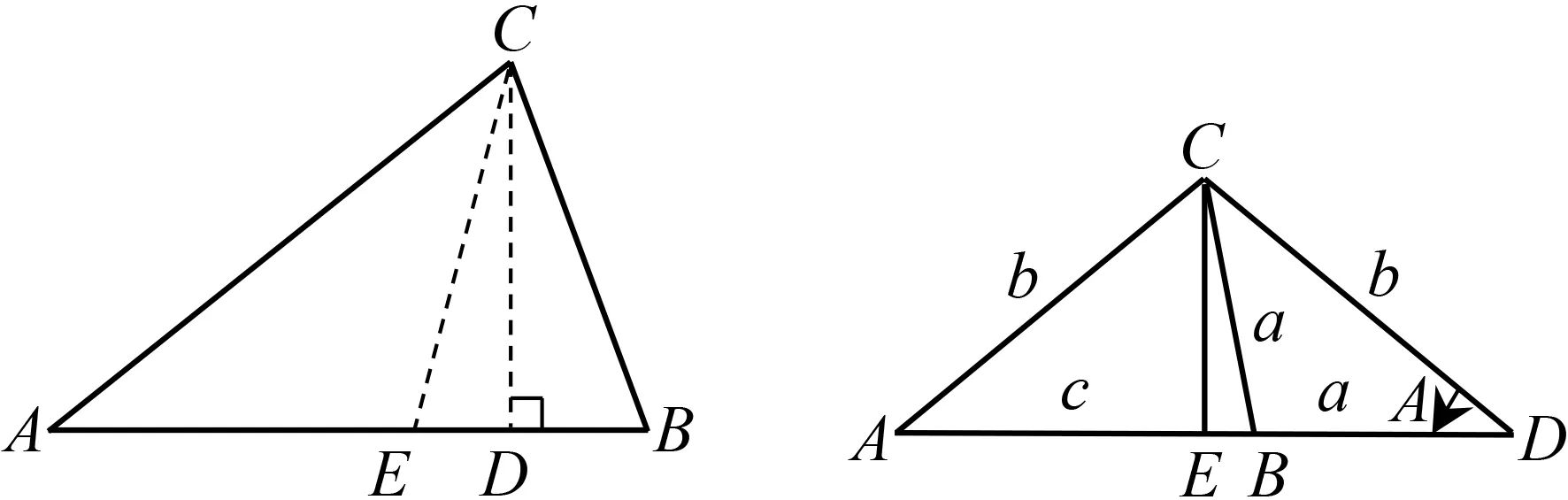
图1 图2

点评通过观察数式的代数、几何结构，引导学生从不同角度，运用不同方法思考、联想，体现数学思维的灵活性与敏捷性；有目的地对学生进行发散思维的训练，培养学生养成“大胆猜想，小心论证”的好习惯，提升数学解题运算能力．由此可见，充分观察数式的结构，才能在数学解题中实现“落霞与孤鹜齐飞，秋水共长天一色”的美好画面．

3 转化数式的代数结构，培养学生运算创新能力

波利亚在《怎样解题》中指出：“困难的问题需要有一种神奇的、不寻常的、崭新的组合．而解题者的才能就在于组合的独创性．”因此，再好的方法，都需要学生独立完成，教师只是学生学习的引导者，起着主导的作用，而学生才是学习的主体．因此，在高三一轮复习过程中，不要一味地追求每节课所讲题目的数量，更重要的是要把每道题目讲得细、讲得透，体现思维的灵活性与创造性.下面以一道试题的复习教学为例，基于转化数式的代数结构，培养学生运算创新能力．

例3(2020年全国高考Ⅰ卷21题)已知函数f(x)=ex+ax2-x．

当a=1时，讨论f(x)的单调性；

分析 对于函数单调性问题，很多学生只要看到函数解析式就开始求导，而后就是令f′(x)=0，但是一遇到困难就不知道怎么下笔了．为什么会出现这样的现象？归根到底还是学生对于数式缺乏观察能力，不能通过分析数式结构，对数学问题进行发现、提出、分析和解决．因此，笔者对本题第(2)问的解答，在教学过程中通过观察对数式结构，对学生进行了如下的启发教学，培养学生运算创新能力．

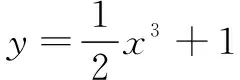
师：很好！那么对于两个数值大小比较问题，我们在哪个章节里面涉及到了呢？

生：在基本不等式的证明中，我们涉及了两个数值的大小比较．

师：那我们还记得课本介绍了哪些证明方法吗？

生：有作差法(作差和0比较)，还有分析法(执果索因)和综合法(由因到果)．

师：太棒了！那么我们能不能尝试作差法呢？

师：经过五分钟探究，请大家告诉老师，能不能解决y=F(x)的最小值呢？

生：不能，ex以及参数a都使得计算非常繁琐．

师：发现问题比解决问题更重要！你们这么快就发现本题的主要矛盾了，那么接下来我们该如何解决呢？

生：我们可以尝试分离参数a．

师：在这个五分钟里，请你们告诉老师，ex与参数a，谁让你们更头疼呢？显然，ex在这个问题中才是本题处理的难点，所以你们有什么好的方法将这个大麻烦解决呢？

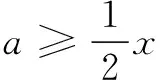
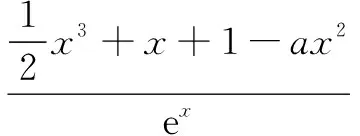
点评 高三数学复习课的目标在于通过数学问题的解决去巩固和加深学生原有知识概念以及数学思想、方法、技能与模型应用能力，促进学生建构完整的知识网络．我们在平时教学过程中需要有目的地引导学生通过观察数式的结构特征去发现和提出问题、分析和解决问题，从而提升其解题运算能力．

4 培养思维辨析能力，提升数学运算能力

众所周知，数学运算能力是数学核心素养的重要内容，通过运算促进数学思维发展，而思维的基本形式有概念、判断、推理；思维的一般过程包括分析与综合、比较与分类、抽象与概括、系统化与具体化，其中分析与综合是思维的基本过程．那么，要提升学生的数学解题运算能力，还应该训练学生的思维辨析能力即分析与综合能力．

分析 本题考查的是向量运算问题，其体现数形结合思想同时也需要转化化归思想，在解决过程中学生展示了以下解法．

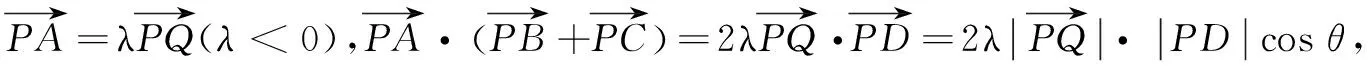
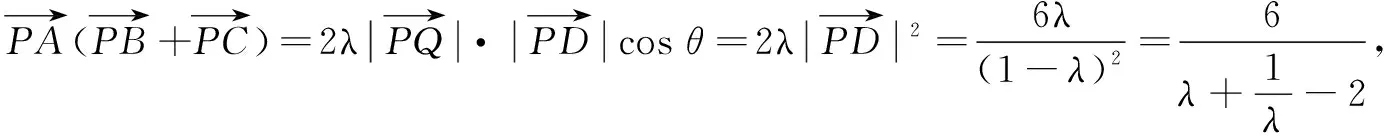
点评在例4的解决过程中，通过观察向量式的结构，从定义、几何表征、代数以及极化恒等式(重要命题)等多个角度让学生体验解题的愉悦感与成就感，体会从数式结构的改变去理解数学的转化与化归思想，提升学生的数学解题运算能力，培养学生的思维辨析能力．

总之，从上面的例题解决策略与笔者多年的一线教学经验以及对江苏新高考的理解中，笔者认为任何一个数学问题的解决过程都可以看成是一个审美赏美的过程，教师要善于引导学生去观察数式结构中的“美”，如解析几何中的“设而不求”、不等式中常用的轮换对称、三角函数中的对偶式、圆锥曲线的统一定义、向量中的极化恒等式……题目中所体现的数式的简洁美(抽象美、符号美、统一美)、和谐美(对称美、形式美)、奇异美(有限美、神秘美)等，让学生发现数式的各种美，培养其观察能力，学会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界；加深学生对数式结构的理解，培育他们热爱数学、热爱科学、热爱生活；让学生在数学解题学习过程中得到愉悦的体验，完善自己的知识结构，形成观察数式结构的习惯，提升运算能力，最终达到提升数学素养的目的．