美术中的数学文化题

童广鹏 (河南省民权县高级中学 476899)

形与数是数学所研究的对象，形数和谐才产生美感.美术追求浪漫，数学追求严谨，二者从远古一路走来，有机结合是历史发展的必然趋势．如今高考要求数学文化融入试题，美术作为重要研究对象，完全契合高考命题主旨．下面以实例分析之．

1 蒙娜丽莎笑开颜

图1

命题背景绘画技巧与科学研究的结合，造就出举世闻名的瑰宝——世界名画《蒙娜丽莎》，该画作主要表现了女性的典雅和恬静的典型形象，塑造了资本主义上升时期一位城市有产阶级的妇女形象．本题用清晰明确的数学关系将抽象的视觉量化出丰富的内涵，简中见奇，极富魅力．

2 小孩扑枣来盘点

例2如图2，《宋人扑枣图轴》是作于宋朝的中国古代画作，现收藏于中国台北故宫博物院．有甲、乙两人想根据该图编排一个舞蹈，舞蹈中他们要模仿该图中小孩扑枣的爬、扶、捡、顶中的两个动作，每人模仿一个动作，若他们采用抽签的方式来决定谁模仿哪个动作，则甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”的概率是( )．

图2

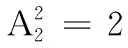
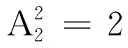
命题背景院角的枣树结实累累，小孩群来攀扯，枝桠不停晃动，粒粒枣子摇落满地，有的牵起衣角，有的捧着盘子拾取，又玩又吃，一片兴高采烈之情，跃然于绢素之上．本题从美术的角度，以中国古画为主线，运用排列组合知识解决问题，不仅有效地突出中华传统文化，更是弘扬社会主义核心价值观的得力途径．

3 结构素描看椭圆

例3美学四大构件是：史诗、音乐、造型(绘画、建筑等)和数学．素描是学习绘画的必要一步，它包括了明暗素描和结构素描，而学习几何体结构素描是学习素描最重要的一步．某中学2019级某同学在画“切面圆柱体”(用与圆柱底面不平行的平面去截圆柱，底面与截面之间的部分叫做切面圆柱体)的过程中，发现“切面”是一个椭圆(图3)．若“切面”所在平面与底面成45°，则该椭圆的离心率为( )．

图3

命题背景切面圆柱体是在圆柱体的基础上，在圆柱体高的大概三等分点处向斜上方边缘切面所得．而在数学中，就是研究椭圆问题．可见美术因为数学变得丰富而美丽，数学因为美术变得形象而直观．

4 名人雕塑美惊叹

例4雕塑成了大学环境中不可分割的一部分，甚至成为大学的象征，在中国科学技术大学校园中就有一座郭沫若的雕像．雕像由像体AD和底座CD两部分组成．如图4，在Rt△ABC中，∠ABC=70.5°，在Rt△DBC中，∠DBC=45°，且CD=2.3 m，则像体AD的高度为( )．

图4

(参考数据：sin 70.5°≈0.943，cos 70.5°≈0.334，tan 70.5°≈2.824)

A．4.0 mB．4.2 mC．4.3 mD．4.4 m

命题背景中国科学技术大学于1958年9月创建于北京，首任校长由郭沫若兼任．1970年初，学校迁至安徽省合肥市．如今在中国科学技术大学东区校园树立有郭沫若铜像雕像，并将该广场命名为郭沫若广场．

5 柳暗花明悬链线

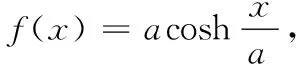
图5

命题背景悬链线是一种曲线，指两端固定的一条(粗细与质量分布)均匀、柔软(不能伸长)的链条在重力的作用下所具有的曲线形状，例如悬索桥等，因其与两端固定的绳子在均匀引力作用下下垂相似而得名．

数学家以深邃的数学眼光评价美，美术家以美学原理、绘画技法、雕塑技巧来创造美，美术与数学的联系可谓自然天成．在可预见的未来，二者更能水乳交融，创造出更多令人叹为观止的美．