生活性·直观性·独创性：构建自主探究的小学数学课堂

王丽慧

（诏安县第一实验小学，福建 漳州 363500）

学生是数学学习和发展的主体，在教学中，教师应以《义务教育数学课程标准（2011 年版）》理念为指导，“创造性地理解和使用教材”［1］，积极创新思路，改进教学策略，营造有利于学生自主、合作和探究学习的课堂氛围，做到“从儿童视角出发，关注儿童的思维特点、心理特征、认知水平、思考习惯、知识经验等富有儿童特性的数学思考”。［2］让学生在掌握数学知识的过程中，激发数学情感，发展思维能力，培育创新精神。

一、生活性：激发数学情感

数学情感是指学生在学习数学的过程中，真切感受数学与生活的广泛联系，形成学习有意义的数学的积极心理情绪。数学知识由于其高度概括性与抽象性的特点，学生常常感到枯燥乏味，容易产生厌学情绪。教师要采用生活化的教学策略，激发学生的数学情感，使他们热情地投入学习中。《数学课程标准解读》指出：“学生学习数学，是学生生活常识的系统化，离不开学生现实的生活经验。”在教学中，要采用生活化情境呈现的方法，营造生动、有趣的问题情境，使数学问题生活化，引领学生从数学的角度观察、思考和解决问题，认识到“数学就在生活中”，感受学习“有用的数学”的乐趣，兴致勃勃地参与问题探究。例如，教学有关“折扣”的知识，课前让学生收集生活中有关“打折”的资料，课堂上出示以下问题：

学校响应“新冠肺炎疫情”防控号召，要买25 瓶洗手液。恒盛、万利、旺城三家超市同时销售一个品牌的洗手液，该品牌原价每瓶为16 元，恒盛超市打“八五”折，万利超市“满300 元打七五折”，旺城超市“买四送一”。请问学校到哪家商店购买最省钱？

学生经过讨论，得出以下几种购买方案：

（1）到恒盛超市购买：16×25×85%=340（元）

（2）到万利超市购买：16×25=400（元），400×75%=300（元）

（3）到旺城超市购买：25÷（4＋1）=5，5×4×16=320（元）

教师启发：哪个方案最为省钱？学生比较后得出：340 元〉320 元〉300 元，所以到万利超市购买最省钱。学生知道哪家超市的“打折”方案更优惠，深入掌握“打折”的数学知识，形成实际数学应用的能力，数学情感得到培养。

二、直观性：优化思维过程

数学学习中的思维过程，指的是学生运用数学知识、原理对问题进行分析、判断，进而有效解决问题的思维活动。优化的思维过程体现数学学习的有效和高效。在教学中，教师积极创设直观化问题情境，“是实施合作学习、自主探究、小组互动的前提条件”。［3］与以往的课本相比，现行数学教材添加了许多数学问题主题插图，化抽象的数量关系、文字信息为直观可感的形象，有利于拓宽思路、活跃思维。小学数学教材编排，其目的在于通过色彩丰富的主题插图，吸引学生的注意力，并使其透过主题插图展示的生活小情景，唤起生活经验，感悟数学基本概念、数量关系及其计算方法，使数学学习思维过程简单化。因此，应该充分发挥主题插图的直观作用，活跃互动氛围，力求简化、优化思维过程，提高学习质量与效率。例如，四年级下册《旅游中的数学》，插图展示以下问题：

四年级师生共32 名去公园划船游玩，请你根据下面的说明，设计一种最省钱的租船方案。大船限乘6 人，租金30 元；小船限乘4 人，租金24 元。

让学生题、图结合，先算单人价格，寻找便宜的租船方案。直观、形象的主题图，直接唤起生活记忆，结合题目中的描述，学生提出：

生1：大船人均5 元，小船人均6 元，租大船比较便宜。

生2：全部租坐大船，有空位，会形成浪费。要看具体人数，才能判断如何租船更便宜。

显然，学生已经能够借助主题图进行细致思考。教师指导列表（表1），比较、确定最优方案：

表1

通过主动交流、讨论，学生经历简洁、明了的思维过程，获得启示：解决这类问题，不仅要考虑哪一种船便宜，还要考虑尽可能地使座位都坐满。运用直观的主题图，化抽象的数量关系为具体可感的形象，学生通过观察、分析、转换解决问题，思维的灵活性得到培养。

三、独创性：培育创新精神

数学创新精神是指学生懂得并且善于综合运用数学知识、技能与方法，探索富有创意的问题解决思路的心理智慧品质。培养学生的创新精神，是新课程改革重要目标之一。在教学中，教师是学习的组织者、引导者与合作者，引导、鼓励学生大胆尝试，敢于探究，善于质疑，表达自己独特的感悟。例如，教学六年下册《圆柱的体积》，设计以下环节：1.将圆柱体教具沿底面直径切分成32 等份。

2.将两个半圆柱教具分别对拼成一个近似的长方体。

3.观察割拼过程，想象：分得份数越来越多，直到足够多份时，所拼成的立体图形最终可以得到一个长方体。

4.比较得出：圆柱体的体积=底面积×高=圆周率×半径的平方×高。

学生通过认真观察、积极思考，进而发现规律，提高解题能力，培养创新精神。

教师再设计以下一道题：

一个圆柱形粮囤，从里面测，它的侧面积是12.56平方米，底面直径是4 米，这个圆柱形粮囤的容积是多少平方米？

学生按常规方法解答如下：

（1）高：12.56÷（3.14×4）=1（米）

（2）体积：4÷2=2（米）

3.14×2×2×1=12.56（立方米）

答：这个圆柱形粮囤的容积是12.56 平方米。

教师启发：“有没有更加简便、高效的方法？”接着，演示圆柱体的体积公式推导过程，把拼成的长方体“放倒”、展开（如图1）：

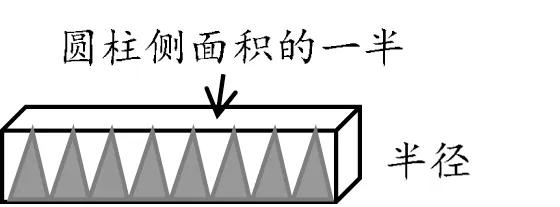
图1

学生得出结论：这个长方体的底面积相当于圆柱体侧面积的一半，高相当于圆柱体的半径。于是，解题思路有所突破：

12.56÷2×（4÷2）=12.56（立方分米）

答：这个圆柱形粮囤的容积是12.56 平方米。

经过比对，学生在问题解决中，灵活调动所学知识来分析题目，创新解题思路，寻求最佳的解题方法。